VI Error correction and practical issues

Errors occur both in computation as well as in communication, and generally degrade information content. In classical computation, typical errors are flipped bits or lost data packages. A primary goal of hardware design is to make such errors unlikely, which can be done, e.g., by utilizing dissipation to stabilize the outcomes of irreversible gate operations. This goal competes with other goals such as speed, capacity, size, stability, longevity, energy consumption, and, of course, costs, which along with practical limitations means that a certain amount of errors must be tolerated. To cope with them, classical computation algorithms and communication protocols introduce a certain amount of overhead (redundancy) into the information. This can be used to detect whether errors have occurred (a step called syndrome diagnosis), and preserves enough of the information so that the errors can be corrected (by recovery operations).

A simple example is the code

$$0_L\to 000,1_L\to 111,$$

which represents one logical bit of information (subscript $L$) in terms of three physical bits. If one of the physical bits is flipped this can be detected by comparison to the other bits, and subsequently corrected following the rules

$$000,001,010,100\to 0_L;011,101,110,111\to 1_L.$$

Following this scheme, only errors affecting two or all three of the physical bits will result in an error of the logical bit. A single-bit error probability $p$ will thus result in an error probability $p^2(3-2p)$ for the logical bit, which is much less than $p$ if $p$ is small.

Classical error correction of many independent single-bit errors can be achieved when $k$ logical bits of information are encoded into a sufficiently large number $n$ of physical bits. The number of differing bits of two code words is called their distance, and the smallest distance occurring in a code is the distance of the code, $d$. Correction of multiple errors then requires to identify the logical code word with the smallest distance to the register state, which is reliable unless the number of errors exceeds $[(d-1)/2]$ (here $[\cdot ]$ denotes the integer part of a number). In other words, $d$ determines the number of erroneous physical bits that can be tolerated for reliable identification of the logical bits. Classical error correction codes of this kind are therefore often characterized by the triple $[n,k,d]$. It should be noted that the distance is a useful characteristic only if the errors are not correlated, i.e., if they only affect one bit at a time. This does not apply, e.g., to a data package loss, which yields undetermined values of a number of consecutive bits. The design of a resilient error correction scheme therefore also depends on an adequate error model, which identifies the types of errors that are most likely to occur.

Quantum computation is sensitive to a wide range of additional types of errors that affect the amplitudes of individual or collective qubit states. The implementation of gates is delicate because of their linear and reversible nature, which prevents the use of dissipation to stabilize the outcomes. In particular, multi-qubit gate operations typically require precise control of interactions, which can also leak on to other qubits. Furthermore, multi-qubit gates tend to propagate errors—e.g., an error in the control bit of a CNOT gate will result in an error of the target bit. To a larger extent than classical codes, therefore, quantum codes must rely on a good error model.

Consider, for example, a system designed to realize the Pauli $X$ gate (NOT) by time evolution with a Hamiltonian $aX$, which must be sustained for a set time $\mathrm{\Delta }t=\mathrm{\hslash }\pi /2a$ (see worksheet 2). Imperfections in the duration of this action will introduce errors into the final states. Furthermore, the physically realized Hamiltonian may differ from $aX$ (e.g., it may feature contributions proportional to $Y$ and $Z$, as well as many-qubit terms arising from interactions), and all terms may fluctuate temporally.

An important source of these contributions is the dynamics of the environment, i.e., all physical components that are not directly participating in the computational tasks. For example, the uncontrolled motion of charge carriers in parts of a device results in a fluctuating electromagnetic field. External influences of this kind are worrisome because they generally cause the state of the quantum register to become mixed: the register state will depend on the environment, and therefore becomes entangled with it; its reduced density matrix will therefore describe a statistical mixture. This phenomenon, called dephasing or decoherence, is undesirable because it negatively affects the usable amount of entanglement (as we have seen on worksheet 2 for the example of the equal mixture of all four Bell states). Even more directly, perturbed relative phases of quantum states also negatively affect their superposition, i.e., quantum parallelism.

Consequently, error correction schemes for quantum information need to cope with a much larger variety of errors—in principle, a continuum of errors, which can affect the phase and magnitude of the amplitudes of the state. Moreover, they cannot establish redundancy by copying the information, which would violate the no-cloning theorem. Surprisingly, resilient quantum error correction strategies not only exist, but also get by with a finite set of diagnosis and recovery operations—a phenomenon known as error discretization.

In order to see how this comes about, let us specialize to single-qubit errors. Such errors can generally be represented by a unitary $2\times 2$ matrix $U=a_{0}I+a_{x}X+a_{y}Y+a_{z}Z$, which transforms an error-free physical qubit state $|\psi ⟩=\alpha |0⟩+\beta |1⟩$ into the defective state $U|\psi ⟩$. The contribution $X$ flips the qubit with a probability depending on the coefficient $a_x$. An individual flip can be detected and corrected by adapting the classical three-bit scheme: Encode the two logical basis states into three physical qubits, such that $|0_L⟩=|000⟩$ and $|1_L⟩=|111⟩$. A logical-qubit state is then described by a physical state $|\psi ⟩=\alpha |000⟩+\beta |111⟩$. This is not a threefold copy of the logical qubit, which would correspond to a separable product state—instead, we here deal with an entangled three-qubit state.

Erroneous flips of the $n$th qubit (due to $X_n$) result in admixture of the other three-qubit basis states. This can be detected by measurements of the error syndromes $S_1=Z_1{Z}_2$ and $S_2=Z_1{Z}_3$, and corrected by applying an operator $U$ following the rules

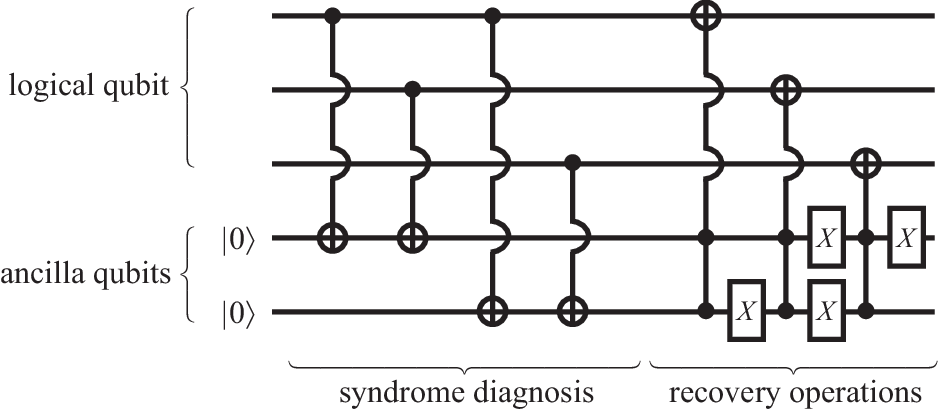
Figure 20 shows how these conditional operations can be achieved without doing any measurements, but instead utilizing CNOT and Toffoli gates involving two ancilla qubits. How does this circuit cope with the continuous set of possible errors? A single-qubit error moves the quantum state into a subspace spanned by the computational basis states with distance 0 and 1 to the logical qubits, and in this basis is specified by four complex amplitudes. In the circuit, these amplitudes simply determine the probabilities that the control bits trigger the various CNOT operations. At the end of the procedure, the complex amplitudes are transferred to the two ancillary qubits, whose joint state also resides in a four-dimensional space.

Analogously, errors of the type $Z$ can be corrected using a three-qubit code $|0_L⟩=|+++⟩$, $|1_L⟩=|---⟩$, where $|\pm ⟩=\sqrt{1/2}(|0⟩\pm |1⟩)$ are the eigenstates of the $X$ operator. Effectively, the roles of $X$ and $Z$ are then interchanged.

Once we can cope with individual $X$ and $Z$ errors, schemes can be fused via concatenation to yield a code that can also correct combined errors. This naturally leads to the Shor code, which uses 9 qubits to encode one logical qubit according to

	$|0_L⟩={\displaystyle \frac{(|000⟩+|111⟩)(|000⟩+|111⟩)(|000⟩+|111⟩)}{2\sqrt{2}}},$
	$|1_L⟩={\displaystyle \frac{(|000⟩-|111⟩)(|000⟩-|111⟩)(|000⟩-|111⟩)}{2\sqrt{2}}}.$

Note how $X$ errors can be detected by comparing three consecutive qubits, while $Z$ errors are detected by the relative phase of every third qubit; the latter can be diagnosed using the syndromes $X_1{X}_2{X}_3{X}_4{X}_5{X}_6$ and $X_4{X}_5{X}_6{X}_7{X}_8{X}_9$.

Since $Y=iXZ$, the Shor code also allows to correct $Y$ errors—therefore, it offers protection against arbitrary single-qubit errors. On the other hand, considering that here $[n,k]=[9,1]$, this is achieved with a rather large overhead. There are more sophisticated codes that achieve the same task with less than 9 qubits, the minimum being 5. This still exceeds what was required classically, and moreover involves many more syndrome diagnosis and recovery operations. Considering that these operations are also prone to errors, it is clear that quantum error correction is still a challenging task.

More general schemes—in particular, codes based on the stabilizer formalism, which utilizes group theory—allow to cope with complex types of errors affecting a collection of qubits, and also take care of errors accumulated by faulty gate operations. If the initial error rate falls below a certain threshold, these codes can be scaled up by adding more and more overhead, thereby allowing (in principle) to achieve arbitrarily good (fault-tolerant) quantum computation. However, while present technology has advanced sufficiently to enable reliable quantum communication, a universal quantum computer is still far removed from reality.

This brief concluding section juxtaposes the main technological requirements for a workable quantum computer and the key features of some specific physical implementations.

As is clear from the preceding section, quantum information processing poses serious technical challenges. E.g., fault tolerant computation requires that the error rate of gate operations falls below a certain threshold, and can only be implemented when the system can be scaled up by adding more and more components. The various challenges have been canonized by diVincenzo into a set of five core requirements, which are known as the DiVinzenco criteria:

• 1.

  Well-defined qubits. This requires to identify physical systems whose quantum dynamics is essentially constrained to two quantum levels. Examples for naturally occurring two-level systems are the spin of electrons and certain nuclei, as well as the polarization of photons. In many proposed systems, however, the reduction to two levels is only approximate. Examples are atoms in ion traps, photons stored in microcavities, the magnetic flux penetrating a superconducting ring, and electrons confined to (normal conducting or superconducting) solid-state devices, such as quantum dots. In all these cases, care has to be taken that the system does not populate the other available energy levels (i.e., one needs to avoid leakage), which can be best done by making these levels energetically inaccessible.

  It is of course possible to design quantum computation schemes that are not binary, and therefore make use of more than two levels in the energetically accessible range $\mathrm{\Delta }E$ of the register components. However, adding qubits provides much better scalability. Each additional qubit multiplies the register state dimension by a factor of two (resulting in $2^N$ levels), and each qubit can be addressed individually, which requires energy resolution $\sim \mathrm{\Delta }E/N$ instead of resolution $\sim \mathrm{\Delta }E/2^N$ for a comparable multi-level system.

  By convention, if there is a clear energy separation between the two levels, the state with the lower energy is designated $|0⟩$, and the state with the higher energy is designated $|1⟩$. As discussed in the context of error correction, the physical qubits can then be used to encode logical qubits, which allows to take care of the most likely sources of errors specific to the chosen implementation.

• 2.

  Initialization to a pure state. The quantum register must start in a well-defined state. It is sufficient to have a reliable method to prepare at least one such state, since a universal quantum computer would be able to transform this into any other state. Utilities to prepare a larger variety of states further improves the efficiency of quantum computation.

  Using the convention of labeling qubit levels according to their energy, the register state $|0⟩$ often corresponds to the ground state of the system. This state can be prepared by allowing the system to equilibrate (relax) at low temperature. Other states may be enforced by relaxation in presence of external fields (such as a magnetic field for nuclear spins), or dynamically (e.g., by pumping of atomic transitions).

  It is not necessary, however, that the preparation process is deterministic. E.g., a viable strategy is to make a hard, complete measurement of the register, thereby forcing it into a pure state that is completely determined by the recorded measurement outcomes.

  If initialization is not perfect, it can be combined with error correction schemes to enhance its accuracy. In particular, if the state is not entirely pure, the entropy can be transferred into ancilla qubits, so that the register state become purified. Such procedures also allow to carry out initialization in multiple steps.

• 3.

  Universal set of quantum gates. As discussed in section III, a universal set of quantum gates can be obtained using single-qubit rotations on the Bloch sphere, and at least one type of two-qubit operations (such as CNOT). Alternative constructions use a sufficiently large number of multi-qubit gates. Using facilities to swap qubits, it is not necessary that each pair of qubits can be coupled directly; still, the coupling network needs to be sufficiently interconnected, and also should be scalable to a large number of qubits. This is a severe problem for many proposed implementations.

  For each implementation, the precision of gate operations can be increased not only via error correction, but also using insight into the specific quantum dynamics of the system. E.g., echo and refocussing techniques in nuclear magnetic resonance employ judiciously timed magnetic-field pulses to average out the effects of spurious qubit couplings and unwanted single-qubit terms in the Hamiltonian. This exemplifies the natural tradeoff between precision and speed of gate operations, which is a general obstacle in all implementations.

• 4.

  Qubit-specific measurement. Ideally, to determine the outcome of a computation one should be able to carry out ideal measurements on each physical qubit. In practice, a finite degree of imperfection can be tolerated. This may be because the computation can be repeated, or because it can be carried out on many systems in parallel. An interesting simplification occurs because algorithms often use quantum parallelism only during the calculation, but are designed to deliver a classical bit sequence $x_n$ as output. Such results can be amplified using a quantum fanout operation of the type $\alpha |x_1⟩|00⟩+\beta |x_2⟩|00⟩\to \alpha |x_1{x}_1{x}_1⟩+\beta |x_2{x}_2{x}_2⟩$, which enhances the measurement fidelity because the desired information is now encoded in additional qubits. (Note how the fanout operation differs from a copy operation prohibited by the no-cloning theorem; rather, it closely resembles error correction procedures.)

• 5.

  Long coherence times. This statement subsumes various requirements for the protection of the quantum register state throughout the computation. In particular, one needs to preserve the capacity to use superposition and entanglement as computational resources. As discussed before, this capacity is in particular degraded by spurious internal and external interactions. These effects can be broadly categorized depending on whether they affect the population probabilities or interference of the register states (i.e., the modulus or complex phase of the amplitudes): Relaxation (on a time scale $T_1$) affects the probabilities, and often is combined with energy loss or gain (dissipation). Dephasing (on a time scale $T_2$) affects the phases, and generally reduces the purity and entanglement of the register state (decoherence).

  In most systems, $T_1\gg T_2$, i.e., the operability is limited by dephasing. A viable quantum computer needs to carry out $>10000$ gate operations during this time. The polarization of photons and the spin of electrons in solid-state devices are two types of qubits which possess reasonably long dephasing times (the latter lends a main incentive to the field of spintronics). On the other end of the scale, charge (as, e.g., carried by electrons confined in a quantum dot) couples strongly to electromagnetic fluctuations, which discounts this degree of freedom for quantum computation purposes.

These requirements are supplemented by two additional criteria for reliable quantum communication:

• 6.

  Convert stationary and flying qubits. Stationary qubits reside in registers, while flying qubits propagate along quantum transmission lines. Photons make ideal flying qubits, while nuclei and atoms typically serve as stationary qubits. In this respect, electrons in solid state devices are particularly flexible because they can move through conducting regions, but can also be confined electrostatically.

• 7.

  Transmit flying qubits between distant locations. This can be achieved with high fidelity for photons, but is far more challenging for electrons. In spintronics, e.g., the electronic spin can be flipped by scattering off magnetic impurities in the transmission line.

At present, none of the various physical candidate platforms score well on all of the core requirements. The key challenge is to overcome the natural trade-off between easy access of qubits (initialization, control, readout), a high degree of isolation (coherence), and scalability. On the other hand, this trade-off can also be exploited to balance strengths in certain areas (e.g., a long coherence time) against weaknesses in other areas (e.g., imprecise gates, whose errors can then be corrected by running a more sophisticated, time-consuming error correction scheme). That said, any viable quantum computer is likely to be a hybrid device which combines the specific strengths of the various physical platforms.