IV Quantum Communication

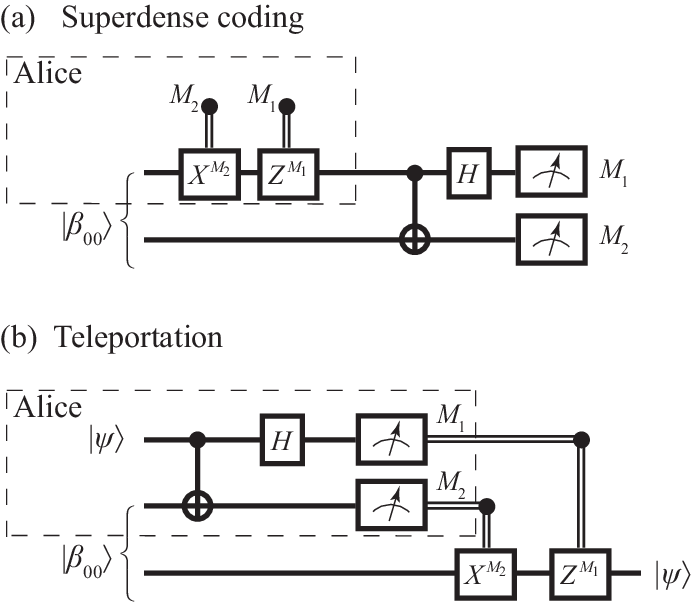
Superdense coding is a simple scheme which illustrates how entanglement can facilitate the transmission of information. The scheme is illustrated in Fig. 9(a). Here and in the following, double-lines indicate classical transmission or control channels. By convention, sender and receiver are designated the names Alice and Bob (or A and B), respectively. Initially, Alice and Bob each are in possession of a single qubit. In the distant past (say), they met and prepared these qubits in the entangled Bell state $|{\beta }_{00}⟩=\frac{1}{\sqrt{2}}(|00⟩+|11⟩)$. Now, Alice and Bob are located at distant locations (this handed down tale is intended to convey how the scheme will exceed classical expectations, but most of these embellishments are not necessary—e.g., A&B could have received their entangled qubits from an appropriate, distantly located two-photon source). Alice can now decide whether she wishes to carry out two operations on her qubit—first a NOT operation ($X$), then a phase flip ($Z$). This results in the state $Z_1^{M_1}{X}_1^{M_2}|{\beta }_{00}⟩$, where $M_i=1$ if the operation was carried out, and $M_i=0$ if it was not carried out. Considering each case separately, we see that this transforms the state into $|{\beta }_{M_1{M}_2}⟩$, i.e., into one of the four Bell states. Alice then sends her qubit—just the single one—to Bob, who can use a CNOT and a Hadamard gate to transform the qubit pair back to the computational basis states, $H_1{C}_{12}|{\beta }_{M_1{M}_2}⟩=|M_1{M}_2⟩$ [this is just the inverse of the entanglement procedure in Fig. 6(a)]. A measurement of both qubits in the computational basis therefore allows him to infer both $M_1$ and $M_2$. In effect, using entanglement as a resource, Alice has sent Bob two bits of information.

Quantum teleportation addresses the task of transferring the unknown and arbitrary state of one qubit to another, possibly distant qubit. Because of the no-cloning theorem, this requires to erase all information from the first qubit. How this can be achieved is shown in Fig. 9(b). Before considering the details, note the striking similarities to the circuit for superdense coding—most notably, Alice and Bob again share a Bell pair, and the set of operations they carry out is just interchanged. However, Alice is now also in possession of an extra qubit, whose state $|\psi ⟩=\alpha |0⟩+\beta |1⟩$ she wishes to transmit to Bob. She does not know the complex amplitudes $\alpha$ and $\beta$, and she cannot send the qubit itself, but she can send classical information along a transmission line (e.g., by phone). To succeed, she first entangles the two qubits in her possession by applying a CNOT and a Hadamard gate. This results in the three-qubit state

	$H_1{C}_{12}|\psi ⟩|{\beta }_{00}⟩$	$=$	${\displaystyle \frac{1}{2}}[\alpha (|0⟩+|1⟩)(|00⟩+|11⟩)$
			$+\beta (|0⟩-|1⟩)(|10⟩+|01⟩)]$
		$=$	${\displaystyle \frac{1}{2}}[|00⟩(\alpha |0⟩+\beta |1⟩)+|01⟩(\alpha |1⟩+\beta |0⟩)$
			$+|10⟩(\alpha |0⟩-\beta |1⟩)+|11⟩(\alpha |1⟩-\beta |0⟩)],$

where the second line follows by reordering the terms. Next she measures the two qubits in her possession, and sends her measurement results $M_1$ and $M_2$ to Bob. This allows him to infer how the post-measurement state $|\phi ⟩$ of his qubit is related to the former state $|\psi ⟩$:

	$M_1{M}_2=00$	$\Rightarrow$	$\mathrm{\hspace{1em}}|\phi ⟩=\alpha |0⟩+\beta |1⟩=|\psi ⟩$
	$M_1{M}_2=01$	$\Rightarrow$	$\mathrm{\hspace{1em}}|\phi ⟩=\alpha |1⟩+\beta |0⟩=X|\psi ⟩$
	$M_1{M}_2=10$	$\Rightarrow$	$\mathrm{\hspace{1em}}|\phi ⟩=\alpha |0⟩-\beta |1⟩=Z|\psi ⟩$
	$M_1{M}_2=11$	$\Rightarrow$	$\mathrm{\hspace{1em}}|\phi ⟩=\alpha |1⟩-\beta |0⟩=XZ|\psi ⟩.$

Therefore, in order to obtain $|\psi ⟩$, he simply applies $Z^{M_1}{X}^{M_2}$ to his qubit.

Secure quantum communication schemes rely on the no-cloning theorem, which prevents an eavesdropper (’Eve’) to listen to a communication line (either, Eve will not acquire any information, or her actions can be detected).

Secure communication based on superdense coding.—If Eve would intercept the qubit sent between Alice and Bob, she only possesses a qubit with reduced density matrix $\frac{1}{2}\widehat{I}$, which is independent on the two bits $M_1$ and $M_2$ that Alice is sending. However, Eve could still send an arbitrary qubit to Bob, which would result in him obtaining random values for $M_1$ and $M_2$, as well. This can be detected when Alice and Bob compare parts of their messages.

Quantum key distribution.—To make communication both secure and reliable, one can generate an encryption key shared by Alice and Bob. The message can then be sent classically using a simple encryption technique (e.g., by using XOR operations, which flips bits according to a shared sequence of 0’s and 1’s.).

(a) The BB84 protocol (due to Bennett and Brassard) is a protocol that does not require entanglement. Alice prepares qubits randomly in one of the following four states:

$$|0⟩,|1⟩,|\pm ⟩=\sqrt{1/2}(|0⟩\pm |1⟩).$$

These are the eigenstates of the $Z$ and $X$ operator. Alice makes sure that she uses a preparation method that tells her which state she has prepared (e.g., this can be done by making random $X$ and $Z$ measurements on qubits with density matrix $\widehat{\rho }=\frac{1}{2}\widehat{I}$). She then sends these qubits to Bob, who, for each qubit, randomly measures either $X$ or $Z$. When he measures $X$ and the qubit was in state $|+⟩$, he will obtain 1 with certainty, while if the state was $|-⟩$, he will obtain $-1$ with certainty. If the state was $|0⟩$ or $|1⟩$, he will obtain 1 or $-1$ with 50% probability. In contrast, if Bob measures $Z$, he will obtain certain measurement outcomes 1 and $-1$ for the states $|0⟩$ and $|1⟩$, respectively, while the states $|\pm ⟩$ result in random measurement outcomes. Bob now tells Alice which measurements he did for each qubit, and Alice tells Bob which measurements she did to prepare the qubits (they only communicate the type of measurement, $X$ or $Z$, but not their outcomes). For these instances, their measurements will have resulted in the same outcome, which results in a shared sequence of 0’s and 1’s that they can use for encryption.

An eavesdropper listening to the key distribution would be able to make measurements on an intercepted qubit, but without knowledge of its preparation would not be able to then forward the same qubit to Bob. This would introduce errors into the key (at a rate of 25%), which can be detected when Alice and Bob compare small samples of their key (this part of the key would then be discarded).

The BB84 scheme is simple and robust, and has been implemented experimentally using photons, for which the four states correspond to polarizations in $\widehat{x}$, $\widehat{y}$, $\widehat{x}+\widehat{y}$, and $\widehat{x}-\widehat{y}$ direction. (E.g., in 1997, the scheme was demonstrated using a 23 km long transmission line beneath Lake Geneva.)

(b) The EPR protocol (due to Eckert) uses pairwise entangled qubits prepared in the Bell state $|{\beta }_{00}⟩=\sqrt{\frac{1}{2}}(|00⟩+|11⟩)$, which can also be written as $|{\beta }_{00}⟩=\sqrt{\frac{1}{2}}(|+⟩|+⟩+|-⟩|-⟩)$. Alice and Bob make random measurements of $X$ and $Z$ on each of their qubits, and then communicate to each other to find out for which qubits they did the same measurement. For each of these instances, they are then guaranteed to have found the same outcome. Again, an eavesdropper would introduce errors, and can be detected by sacrificing a small random sample of the key.

In combination with classical encoding schemes that encode messages into longer bit sequences (see error correction, in section VI.1) these protocols can be made reliable against a finite error rate, and secure even against sophisticated eavesdroppers attacks that involve the collective manipulation of the whole qubit stream.