Home page for accesible maths 11.7 Summary 11.7 Summary 12.3 Likelihood Examples: continuous parameters

Style control - access keys in brackets

Font (2 3) - + Letter spacing (4 5) - + Word spacing (6 7) - + Line spacing (8 9) - +

Chapter 12 Introduction to Likelihood Inference

12.1 Motivation

12.3 Likelihood Examples: continuous parameters

We now explore examples of likelihood inference for some common models.

TheoremExample 12.3.1 Accident and Emergency

Accident and emergency departments are hard to manage because patients arrive at random (they are unscheduled). Some patients may need to be seen urgently.

Excess staff (doctors and nurses) must be avoided because this wastes NHS money; however, A&E departments also have to adhere to performance targets (e.g. patients dealt with within four hours). So staff levels need to be ‘balanced’ so that there are sufficient staff to meet targets but not too many so that money is not wasted.

A first step in achieving this is to study data on patient arrival times. It is proposed that we model the time between patient arrivals as iid realisations from an Exponential distribution.

Why is this a suitable model?

What assumptions are being made?

Are these assumptions reasonable?

Suppose I stand outside Lancaster Royal Infirmary A&E and record the following inter-arrival times of patients (in minutes):

18.39, 2.70, 5.42, 0.99, 5.42, 31.97, 2.96, 5.28, 8.51, 10.90.

As usual, the first thing we do is look at the data!

⬇

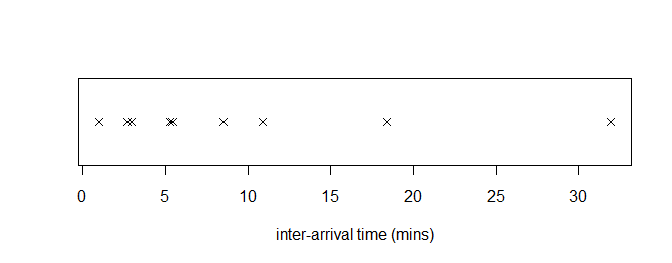
arrive<-c(18.39,2.70,5.42,0.99,5.42,31.97,2.96,5.28,8.51,10.90)

stripchart(arrive,pch=4,xlab="inter-arrival time (mins)")

The exponential pdf is given by

f(x)=\lambda\exp(-\lambda x),

for $x\geq 0$ , $\lambda\geq 0$ . Assuming that the data are iid, the definition of the likelihood function for $\lambda$ gives us, for general data $x_{1},\ldots,x_{n}$ ,

{\color[rgb]{1,1,1}L(\lambda)=\prod_{i=1}^{n}\lambda\exp(-\lambda x_{i}).}

Note: we usually drop the ‘ $|{\bf x}$ ’ from $L(\lambda|{\bf x})$ whenever possible.

Usually, when we have products and the parameter is continuous, the best way to find the MLE is to find the log-likelihood and differentiate.

So the log-likelihood is

	$\displaystyle l(\lambda)$	$\displaystyle=\sum_{i=1}^{n}\log\left\{\lambda\exp(-\lambda x_{i})\right\}$
		$\displaystyle=\sum_{i=1}^{n}\left\{\log(\lambda)-\lambda x_{i}\right\}$
		$\displaystyle=n\log(\lambda)-\lambda\sum_{i=1}^{n}x_{i}.$

Now we differentiate:

{\color[rgb]{1,1,1}\frac{\partial}{\partial\lambda}l(\lambda)=l^{\prime}(% \lambda)=\frac{n}{\lambda}-\sum_{i=1}^{n}x_{i}.}

Now solutions to $l^{\prime}(\lambda)=0$ are potential MLEs.

1

${\color[rgb]{1,1,1}\frac{n}{\hat{\lambda}}-\sum_{i=1}^{n}x_{i}=0,}$
2

${\color[rgb]{1,1,1}\hat{\lambda}=\frac{n}{\sum_{i=1}^{n}x_{i}}=\frac{1}{\bar{x% }}.}$

To ensure this is a maximum we check the second derivative is negative:

\frac{\partial^{2}}{\partial\lambda^{2}}l(\lambda)=l^{\prime\prime}(\lambda)=-% \frac{n}{\lambda^{2}}<0.

So the solution we have found is the MLE, and plugging in our data we find (via 1/mean(arrive))

\hat{\lambda}=0.108.

Now that we have our MLE, we should check that the assumed model seems reasonable. Here, we will use a QQ-plot.

⬇

#MLE of lambda (rate)

lam<-1/mean(arrive)

#1/(n+1), 2/(n+1),..., n/(n+1).

quant<-seq(from=1/11,to=10/11,length=10)

#produce QQ-plot

qqplot(qexp(quant,rate=lam),arrive,xlab="Theoretical

quantiles",ylab="Actual")

#add line of equality

abline(0,1)

Given the small dataset, this seems ok – there is no obvious evidence of deviation from the exponential model.

Knowing that the exponential distribution is reasonable, and having an estimate for its rate, is useful to calculate staff scheduling requirements in the A&E.

Extensions of the idea consider flows of patients through the various services (take Math332 Stochastic Processes and/or the STOR-i MRes for more on this).

TheoremExample 12.3.2 Is human body temperature really 98.6 degrees Fahrenheit?

In an article by Mackowiak et al.³³Mackowiak P.A., Wasserman, S.S. and Levine, M.M. (1992) A Critical Appraisal of 98.6 Degrees F, the Upper Limit of the Normal Body Temperature and Other Legacies of Carl Reinhold August Wunderlich, the authors measure the body temperatures of a number of individuals to assess whether true mean body temperature is 98.6 degrees Fahrenheit or not. A dataset of $130$ individuals is available in the normtemp dataset. The data are assumed to be normally distributed with standard deviation $0.73$ .

Why is this a suitable model?

What assumptions are being made?

Are these assumptions reasonable?

What do the data look like?

The plot can be produced using

⬇

> load("normtemp.Rdata")

> hist(normtemp$temperature)

The histogram of the data is reasonable, but there might be some skew in the data (right tail).

The normal pdf is given by

f(x|\mu,\sigma)=\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\left\{-\frac{(x_{i}-\mu)^{% 2}}{2\sigma^{2}}\right\},

where in this case, $\sigma$ is known.

The likelihood is then

	$\displaystyle L(\mu\|x_{1},\ldots,x_{n})$	$\displaystyle=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\left\{-\frac{% (x_{i}-\mu)^{2}}{2\sigma^{2}}\right\}$
		$\displaystyle=\left(2\pi\sigma^{2}\right)^{-n/2}\exp\left\{-\sum_{i=1}^{n}% \frac{(x_{i}-\mu)^{2}}{2\sigma^{2}}\right\}.$

Since the parameter of interest (in this case $\mu$ ) is continuous, we can differentiate the log-likelihood to find the MLE:

l(\mu)=-\frac{n}{2}\log(2\pi\sigma^{2})-\frac{1}{2\sigma^{2}}\sum_{i=1}^{n}(x_% {i}-\mu)^{2}

and so

l^{\prime}(\mu)=-\frac{1}{2\sigma^{2}}\sum_{i=1}^{n}(-2)(x_{i}-\mu).

For candidate MLEs we set this to zero and solve, i.e.

	$\displaystyle\frac{1}{\sigma^{2}}\sum_{i=1}^{n}x_{i}-n\hat{\mu}$	$\displaystyle=0$
	$\displaystyle\sum_{i=1}^{n}x_{i}-n\hat{\mu}$	$\displaystyle=0$

and so the MLE is $\hat{\mu}=\bar{x}$ .

This is also the “obvious” estimate (the sample mean). To check it is indeed an MLE, the second derivative of the log-likelihood is

l^{\prime\prime}(\mu)=-n<0,

which confirms this is the case.

Using the data, we find $\hat{\mu}=\bar{x}=98.25$ .

This might indicate evidence for the body temperature being different from the assumed 98.6 degrees Fahrenheit.

We now check the fit:

⬇

> temps <-normtemp$temperature # for shorthand

> mean(temps)

[1] 98.24923

> stdtemp = (temps - mean(temps))/0.73

> qqnorm(stdtemp)

> abline(0,1) # add "ideal" fit line y = x

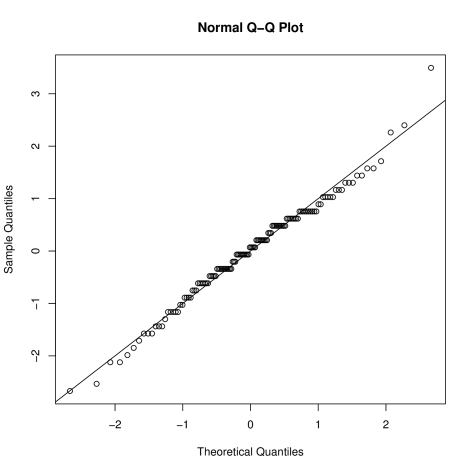
The fit looks good – although (as the histogram previously showed) there is possibly some mild right (positive) skew, indicated by the quantile points above the $y=x$ line.

Why might the QQ-plot show the “stepped” behaviour of the points?

TheoremExample 12.3.3

Every day I cycle to Lancaster University, and have to pass through the traffic lights at the crossroads by Booths (heading south down Scotforth Road). I am either stopped or not stopped by the traffic lights. Over a period of a term, I cycle in 50 times. Suppose that the time I arrive at the traffic lights is independent of the traffic light sequence.

On 36 of the 50 days, the lights are on green and I can cycle straight through. Let $\theta$ be the probability that the lights are on green. Write down the likelihood and log-likelihood of $\theta$ , and hence calculate its MLE.

With the usual iid assumption we see that, if $R$ is the number of times the lights are on green then $R\sim\textrm{Binomial}(50,\theta)$ . So we have

\Pr[R=36]={50\choose 36}\theta^{36}(1-\theta)^{14}.

We therefore have, for general $r$ and $n$ ,

L(\theta)={n\choose r}\theta^{r}(1-\theta)^{n-r},

and

l(\theta)={\color[rgb]{1,1,1}K+r\log(\theta)+(n-r)\log(1-\theta)}.

Solutions to $l^{\prime}(\theta)=0$ are potential MLEs:

l^{\prime}(\theta)={\color[rgb]{1,1,1}\frac{r}{\theta}-\frac{n-r}{1-\theta}},

and if $l^{\prime}(\hat{\theta})=0$ we have

	$\displaystyle\frac{r}{\hat{\theta}}=$	$\displaystyle\ \frac{n-r}{1-\hat{\theta}}$
	$\displaystyle\vspace{.5cm}\mbox{i.e.}\qquad\hat{\theta}=$	$\displaystyle\ \frac{\lx@stackrel{{\scriptstyle\phantom{M}}}{{r}}}{n}.$

For this to be an MLE it must have negative second derivative.

l^{\prime\prime}(\theta)=-\frac{r}{\theta^{2}}-\frac{n-r}{(1-\theta)^{2}}<0.

In particular we have $r=36$ and $n=50$ so $\hat{\theta}=36/50$ is the MLE.

Now suppose that over a two week period, on the 14 occasions I get stopped by the traffic lights (they are on red) my waiting times are given by (in seconds)

4.2,6.9,13.7,2.8,19.3,10.4,1.0,19.4,18.6,0.6,4.5,12.9,0.5,16.0.

Assume that the traffic lights remain on red for a fixed amount of time $t_{r}$ , regardless of the traffic conditions.

Given the above data, write down the likelihood of $t_{r}$ , and sketch it. What is the MLE of $t_{r}$ ?

We are going to assume that these waiting times are drawn independently from $\operatorname{Uniform}[0,t_{r}]$ , where $t_{r}$ is the parameter we wish to estimate.

Why is this a suitable model?

What assumptions are being made?

Are these assumptions reasonable?

Constructing the likelihood for this example is slightly different from those we have seen before. The pdf of the $\operatorname{Uniform}(0,t_{r})$ distribution is

f(x)=\left\{\begin{array}[]{ll}t_{r}^{-1}&\quad 0\leq x\leq t_{r}\\ 0&\quad\text{otherwise}\end{array}\right.

The unusual thing here is that the data enters only through the boundary conditions on the pdf. Another way to write the above pdf is

{\color[rgb]{1,1,1}f(x)=t_{r}^{-1}\mathbf{1}[0\leq x\leq t_{r}],}

where $\mathbf{1}$ is the indicator function.

For data $x_{1},\ldots,x_{n}$ , the likelihood function is then

L(t_{r})={\color[rgb]{1,1,1}\prod_{i=1}^{n}t_{r}^{-1}\mathbf{1}[0\leq x_{i}% \leq t_{r}]}.

We can write this as

	$\displaystyle L(t_{r})$	$\displaystyle=\ t_{r}^{-n}\mathbf{1}\left[\{0\leq x_{1}\leq t_{r}\}\bigcap% \dots\bigcap\{0\leq x_{n}\leq t_{r}\}\right]$
		$\displaystyle=\ t_{r}^{-n}\mathbf{1}[\max(x_{i})\leq t_{r}].$

For our case we have $n=14$ and $\max(x_{i})=19.4$ , so $L(t_{r})=t_{r}^{-14}\mathbf{1}[19.4\leq t_{r}]$ .

We are next asked to sketch this MLE. In R,

⬇

> maxx<-19.4

> #values of t_r to plot

> t<-seq(from=18,to=22,length=1000)

> #likelihood function

> uniflik<-function(t){

> t^(-14)*(t>=19.4)

> }

> plot(t,uniflik(t),type="l")

From the plot it is clear that $\hat{t}_{r}=19.4=\max(x_{i})$ , since this is the value that leads to the maximum likelihood. Notice that solving $l^{\prime}(t_{r})=0$ would not work in this case, since the likelihood is not differentiable at the MLE.

However, on the feasible range of $t_{r}$ , i.e. $\max(x_{i})\leq t_{r}$ , we have

l(t_{r})=-n\log(t_{r}),

and so

l^{\prime}(t_{r})=-n/t_{r}.

Remember that derivatives express the rate of change of a function. Hence since the (log-)likelihood is negative ( $t_{r}>0$ is strictly positive), then the likelihood is decreasing on the feasible range of parameter values.

Since we are trying to maximise the likelihood, this means we should take the minimum over the feasible range as the MLE. The minimum value on the range $\max(x_{i})\leq t_{r}$ is $\hat{t}_{r}=\max(x_{i})=19.4$ .

12.4 Likelihood Examples: discrete parameters

One case where differentiation is clearly not the right approach to use for maximisation is when the parameter of interest is discrete.

TheoremExample 12.4.1 Illegal downloads

A computer network comprises of $m$ computers. The probability of one of these computers to store illegally downloaded files is $0.3$ , independent for each computer. In a particular network it is found that exactly one computer contains illegally downloaded files. Our parameter of interest is $m$ .

What is a suitable model for the data?

What assumptions are being made?

Are these assumptions reasonable?

What is the likelihood of $m$ ?

Let $X\sim Bin(m,0.3)$ be the number of computers in the network that contains illegally downloaded files. Then $\Pr(\text{obs}|m)$ is

L(m)=\Pr(X=1|m)={m\choose 1}0.3^{1}\times 0.7^{m-1}=\frac{0.3}{0.7}0.7^{m}m.

Note that the possible values $m$ can take are $m=1,2,\ldots$ . We can sketch the likelihood for a suitable range of values:

⬇

> mrange<-0:20 # value for m=0 will be zero

> plot(mrange,dbinom(1,mrange,0.3),xlab="m",ylab="L(m)")

From the plot, we can see that the MLE for $m$ is $\hat{m}=3$ . Alternatively, from the likelihood we have

\frac{L(m+1)}{L(m)}=\frac{0.3^{1}\times 0.7^{m}(m+1)}{0.3^{1}\times 0.7^{m-1}m% }=\frac{0.7(m+1)}{m}.

The likelihood is increasing for $L(m+1)>L(m)$ , which is equivalent to $m<7/3$ .

To maximize the likelihood, we want the largest (integer) value of $m$ satisfying this constraint, i.e. $m=2$ , hence $\hat{m}=3$ .

Relative Likelihood intervals

The ratio between two likelihood values is useful to look at for other reasons.

Definition.

Suppose we have data $x_{1},\ldots,x_{n}$ , that arise from a population with likelihood function $L(\theta)$ , with MLE $\hat{\theta}$ . Then the relative likelihood of the parameter $\theta$ is

R(\theta)=\frac{L(\theta|{\bf x})}{L(\hat{\theta}|{\bf x})}.

The relative likelihood quantifies how likely different values of $\theta$ are relative to the maximum likelihood estimate.

Using this definition, we can construct relative likelihood intervals which are similar to confidence intervals.

Definition.

A p% relative likelihood interval for $\theta$ is defined as the set

\left\{\theta\left|R(\theta)\geq\frac{p}{100}\right.\right\}.

TheoremExample 12.4.2 Illegal downloads (cont.)

For example a 50% relative likelihood interval for $m$ in our example would be

	$\displaystyle\left\{m\left\|R(m)\geq 0.5\right.\right\}$	$\displaystyle=\left\{m\left\|\frac{0.3^{1}\times 0.7^{m-1}m}{0.3^{1}\times 0.7^% {2}\times 3}\geq 0.5\right.\right\}$
		$\displaystyle=\left\{m\left\|0.7^{m-3}m\geq 1.5\right.\right\}$

By plugging in different values of $m$ , we see that the relative likelihood interval is $\{1,\ldots,7\}$ . The values in the interval can be seen in the figure below.

TheoremExample 12.4.3 Sequential sampling with replacement: Smarties colours

Suppose we are interested in estimating $m$ , the number of distinct colours of Smarties.

In order to estimate $m$ , suppose members of the class make a number of draws and record the colour.

Suppose that the data collected (seven draws) were:

purple, blue, brown, blue, brown, purple, brown.

We record whether we had a new colour or repeat:

New, New, New, Repeat, Repeat, Repeat, Repeat.

Let $m$ denote the number of unique colours. Then the likelihood function for $m$ given the above data is:

L(m|{\bf x_{1}})=1\times\frac{m-1}{m}\times\frac{m-2}{m}\times\frac{3}{m}% \times\frac{3}{m}\times\frac{3}{m}\times\frac{3}{m}.

If in a second experiment, we observed:

New, New, New, Repeat, New, Repeat, New,

then the likelihood would be:

L(m|{\bf x_{2}})=1\times\frac{m-1}{m}\times\frac{m-2}{m}\times\frac{3}{m}% \times\frac{m-3}{m}\times\frac{4}{m}\times\frac{m-4}{m}.

The MLEs in each case are $\hat{m}=3$ and $\hat{m}=8$ .

The plots below show the respective likelihoods.

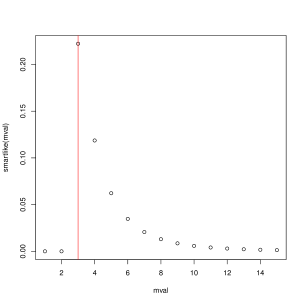R code for plotting these likelihoods:

⬇

> # experiment 1:

> smartlike<-function(m){

> L<-1*(m-1)*(m-2)*(3)*(3)*(3)*(3)/m^6

> }

> mval<-1:15

> plot(mval,smartlike(mval))

> abline(v=3,col=2)

> which.max(smartlike(mval))

⬇

> # Experiment 2:

> # e.g. pink, purple, blue, blue, brown, purple, orange

> smartlike2<-function(m){

> L<-1*(m-1)*(m-2)*(3)*(m-3)*(4)*(m-4)/m^6

> }

> dev.new()

> plot(mval,smartlike2(mval))

> abline(v=8,col=2)

> which.max(smartlike2(mval))

TheoremExample 12.4.4 Brexit opinions

Three randomly selected members of a class of 10 students are canvassed for their opinion on Brexit. Two are in favour of staying in Europe. What can one infer about the overall class opinion?

The parameter in this model is the number of pro-Remain students in the class, $m$ , say. It is discrete, and could take values $0,1,2,\dots,10$ . The actual true unknown value of $m$ is designated by $m_{\text{true}}$ .

Now $\Pr(\text{obs}|m)$ is

\displaystyle\Pr(\text{2 in favour from $m$ and 1 against from $10-m$}).

Now since the likelihood function of $m$ is the probability (or density) of the observed data for given values of $m$ , we have

	$\displaystyle L(m)$	$\displaystyle=\frac{{m\choose 2}{10-m\choose 1}}{{10\choose 3}}$
		$\displaystyle=\frac{m(m-1)(10-m)}{240}$

for $m=2,3,...,9$ .

This function is not continuous (because the parameter $m$ is discrete). It can be maximised but not by differentiation.

⬇

> #likelihood function

> L<-function(m){

> choose(m,2)*choose(10-m,1)/choose(10,3)

> }

> #values of m to plot

> m<-2:9

> plot(m,L(m),pch=4,col="blue")

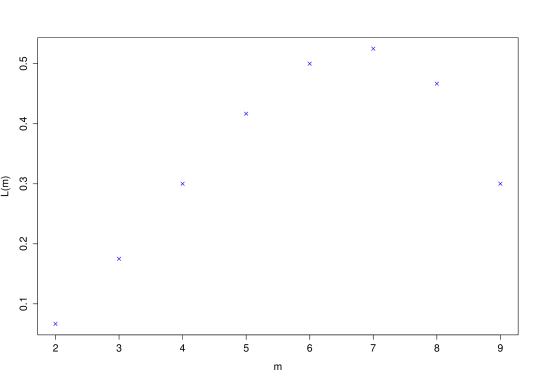
The maximum likelihood estimate is $\hat{m}=7.$ Note that the points are not joined up in this plot. This is to emphasize the discrete nature of the parameter of interest.

The probability model is an instance of the hypergeometric distribution.

12.5 Summary

{mdframed}

A procedure for modelling and inference:

1

Subject-matter question needs answering.
2

Data are, or become, available to address this question.
3

Look at the data – exploratory analysis.
4

Propose a model.
5

Check the model fits.
6

Use the model to address the question.

1

The likelihood function is the probability of the observed data for instances of a parameter. Often we use the log-likelihood function as it is easier to work with. The likelihood is a function of an unknown parameter.
2

The maximum likelihood estimator (MLE) is the value of the parameter that maximises the likelihood. This is intuitively appealing, and later we will show it is a theoretically justified choice. The MLE should be found using an appropriate maximisation technique.
3

If the parameter is continuous, we can often (but not always) find the MLE by considering the derivative of the log-likelihood. If the parameter is discrete, we usually evaluate the likelihood at a range of possible values.

DON’T JOIN UP POINTS WHEN PLOTTING THE LIKELIHOOD FOR A DISCRETE PARAMETER.

DO NOT DIFFERENTIATE LIKELIHOODS OF DISCRETE PARAMETERS!

Chapter 13 Information and Sufficiency

13.1 Introduction

Last time we looked at some more examples of the method of maximum likelihood. When the parameter of interest, $\theta$ , is continuous, the MLE, $\hat{\theta}$ , can be found by differentiating the log-likelihood and setting it equal to zero. We must then check the second derivative of the log-likelihood is negative (at our candidate $\hat{\theta}$ ) to verify that we have found a maximum.

Definition.

Suppose we have a sample ${\bf x}=x_{1},\ldots,x_{n}$ , drawn from a density ${f}({\bf x}|\theta)$ with unknown parameter $\theta$ , with log-likelihood $l(\theta|{\bf x})$ . The score function, $S(\theta)$ , is the first derivative of the log-likelihood with respect to $\theta$ :

S(\theta|{\bf x})=l^{\prime}(\theta|{\bf x})=\frac{\partial}{\partial\theta}l(% \theta|{\bf x}).

This is just giving a name to something we have already encountered.

As discussed previously, the MLE solves $S(\hat{\theta})=0$ . Here, $f({\bf x}|\theta)$ is being used to denote the joint density of ${\bf x}=x_{1},\ldots,x_{n}$ . For the iid case, $f({\bf x}|\theta)=\prod_{i=1}^{n}f(x_{i}|\theta)$ . Also, $l(\theta|{\bf x})=\log f({\bf x}|\theta)$ . This is all just from the definitions.

Definition.

Suppose we have a sample ${\bf x}=x_{1},\ldots,x_{n}$ , drawn from a density ${f}({\bf x}|\theta)$ with unknown parameter $\theta$ , with log-likelihood $l(\theta|{\bf x})$ . The observed information function, $I_{O}(\theta)$ , is MINUS the second derivative of the log-likelihood with respect to $\theta$ :

I_{O}(\theta|{\bf x})=-l^{\prime\prime}(\theta|{\bf x})=-\frac{\partial^{2}}{% \partial\theta^{2}}l(\theta|{\bf x}).

Remember that the second derivative of $l(\theta)$ is negative at the MLE $\hat{\theta}$ (that’s how we check it’s a maximum!). So the definition of observed information takes the negative of this to give something positive.

The observed information gets its name because it quantifies the amount of information obtained from a sample. An approximate 95% confidence interval for $\theta_{\text{true}}$ (the unobservable true value of the parameter $\theta$ ) is given by

{\color[rgb]{1,1,1}\left(\hat{\theta}-\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}},% \hat{\theta}+\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}}\right).}

This confidence interval is asymptotic, which means it is accurate when the sample is large. Some further justification on where this interval comes from will follow later in the course.

What happens to the confidence interval as $I_{O}(\hat{\theta})$ changes?

TheoremExample 13.1.1 Mercedes Benz drivers

You may recall the following example from last year.The website MBClub UK (associated with Mercedes Benz) carried out a poll on the number of times taken to pass a driving test. The results were as follows.

Number of failed attempts	0	1	2	$\geq 3$
Observed frequency	147	47	20	5

Table 13.1: Number of times taken for drivers to pass the driving test.

As always, we begin by looking at the data.

⬇

obsdata<-c(147,47,20,5)

barplot(obsdata,names.arg=c(0:2, or more'),

xlab="Number of failed attempts",

ylab="Frequency",col="orange")

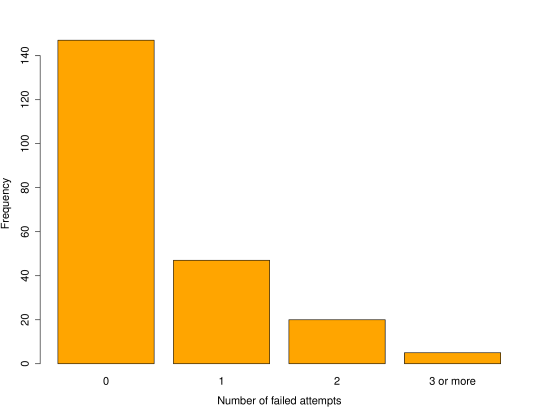
Next, we propose a model for the data to begin addressing the question.

It is proposed to model the data as iid (independent and identically distributed) draws from a geometric distribution.

Why is this a suitable model?

What assumptions are being made?

Are these assumptions reasonable?

The probability mass function (pmf) for the geometric distribution, where $X$ is defined as the number of failed attempts, is given by

\Pr[X=x]=\theta(1-\theta)^{x},

where $x=0,1,2,\dots$ .

Assuming that the people in the ‘3 or more’ column failed exactly three times, the likelihood for general data $x_{1},\ldots,x_{n}$ is

{\color[rgb]{1,1,1}L(\theta)=\prod_{i=1}^{n}\theta(1-\theta)^{x_{i}},}

and the log-likelihood is

	$\displaystyle l(\theta)$	$\displaystyle=\sum_{i=1}^{n}\log\left\{\theta(1-\theta)^{x_{i}}\right\}$
		$\displaystyle=\sum_{i=1}^{n}\{\log(\theta)+x_{i}\log(1-\theta)\}$
		$\displaystyle=n\log(\theta)+\log(1-\theta)\sum_{i=1}^{n}x_{i}.$

The score function is therefore

{\color[rgb]{1,1,1}S(\theta)=l^{\prime}(\theta)=\frac{n}{\theta}-\frac{\sum_{i% =1}^{n}x_{i}}{1-\theta}.}

A candidate for the MLE, $\hat{\theta}$ , solves $S(\hat{\theta})=0$ :

1

${\color[rgb]{1,1,1}\frac{n}{\hat{\theta}}=\frac{\sum_{i=1}^{n}x_{i}}{1-\hat{% \theta}},}$
2

${\color[rgb]{1,1,1}n(1-\hat{\theta})=\hat{\theta}\sum_{i=1}^{n}x_{i},}$
3

${\color[rgb]{1,1,1}n=\hat{\theta}\left(n+\sum_{i=1}^{n}x_{i}\right),}$
4

${\color[rgb]{1,1,1}\hat{\theta}=\frac{n}{n+\sum_{i=1}^{n}x_{i}}.}$

To confirm this really is an MLE we need to verify it is a maximum, i.e. a negative second derivative.

l^{\prime\prime}(\theta)=-\frac{n}{\theta^{2}}-\frac{\sum_{i=1}^{n}x_{i}}{(1-% \theta)^{2}}<0.

In this case the function is clearly negative for all $\theta\in(0,1)$ , if not we would just need to check this is the case at the proposed MLE.

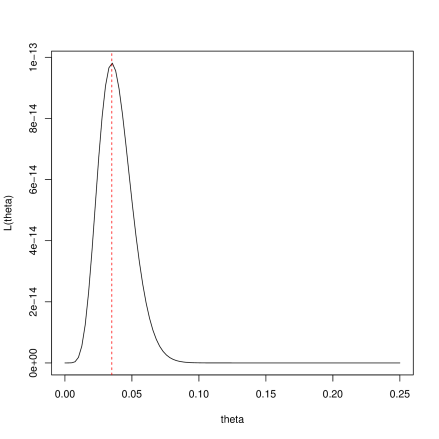
Now plugging in the numbers, $n=219$ and $\sum_{i=1}^{n}x_{i}=0\times 147+1\times 47+2\times 20+3\times 5=102$ , we get

\hat{\theta}=\frac{219}{219+102}=0.682.

This is the same answer as the ‘obvious one’ from intuition.

But now we can calculate the observed information at $\hat{\theta}$ , and use this to construct a 95% confidence interval for $\theta_{\text{true}}$ .

	$\displaystyle I_{O}(\hat{\theta})$	$\displaystyle=-l^{\prime\prime}(\hat{\theta})$
		$\displaystyle=\frac{n}{\hat{\theta}^{2}}+\frac{\sum_{i=1}^{n}x_{i}}{(1-\hat{% \theta})^{2}}$
		$\displaystyle=\frac{219}{0.682^{2}}+\frac{102}{(1-0.682)^{2}}$
		$\displaystyle=1479.5.$

Now the 95% confidence interval is given by

	$\displaystyle(l,u)$	$\displaystyle=\left(\hat{\theta}-\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}},\hat{% \theta}+\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}}\right)$
		$\displaystyle={\color[rgb]{1,1,1}\left(0.682-\frac{1.96}{\sqrt{1479.5}},0.682+% \frac{1.96}{\sqrt{1479.5}}\right)}$
		$\displaystyle={\color[rgb]{1,1,1}(0.631,0.733)}.$

We should also check the fit of the model by plotting the observed data against the theoretical data from the model (with the MLE plugged in for $\theta$ ).

⬇

#value of theta: MLE

mletheta<-0.682

#expected data counts

expdata<-219*c(dgeom(0:2,mletheta),1-pgeom(2,mletheta))

#make plot

barplot(rbind(obsdata,expdata),names.arg=c(0:2, or more'),

xlab="Number of failed attempts",ylab="Frequency",

col=c("orange","red"),beside=T)

#add legend

legend("topright",c("observed","expected"),

col=c("orange","red"),lty=1)

We can do actually do slightly better than this.

We assumed ‘the people in the “3 or more” column failed exactly three times’. With likelihood we don’t need to do this. Remember: the likelihood is just the joint probability of the data. In fact, people in the “3 or more” group have probability

	$\displaystyle\Pr[X\geq 3]$	$\displaystyle=1-(\Pr[X=0]+\Pr[X=1]+\Pr[X=2])$
		$\displaystyle=1-(\theta+(1-\theta)\theta+(1-\theta)^{2}\theta).$

We could therefore write the likelihood more correctly as

L(\theta)=\prod_{i=1}^{n}\Big{\{}\theta(1-\theta)^{x_{i}}\Big{\}}^{z_{i}}\prod% _{i=1}^{n}\Big{\{}1-(\theta+(1-\theta)\theta+(1-\theta)^{2}\theta)\Big{\}}^{1-% z_{i}},

where $z_{i}=1$ if $x_{i}<3$ and $z_{i}=0$ if $x_{i}\geq 3$ .

NOTE: if all we know about an observation $x$ is that it exceeds some value, we say that $x$ is censored. This is an important issue with patient data, as we may lose contact with a patient before we have finished observing them. Censoring is dealt with in more generality MATH335 Medical Statistics.

What is the MLE of $\theta$ using the more correct version of the likelihood?

The term in the second product (for the censored observations) can be seen as a geometric progression with constant term $a=\theta$ and common ratio $r=(1-\theta)$ , and so $\Pr(X\geq 3|\theta)=(1-\theta)^{3}$ (check that this is the case).

Hence the likelihood can be written

	$\displaystyle L(\theta)$	$\displaystyle=\theta^{n_{u}}(1-\theta)^{\sum x_{i}}\left((1-\theta)^{3}\right)% ^{n_{c}}$
		$\displaystyle=\theta^{n_{u}}(1-\theta)^{\sum x_{i}+3n_{c}}$

where the sum of $x_{i}$ ’s only involves the uncensored observations, $n_{u}$ denotes the number of uncensored observations, and $n_{c}$ is the number of censored observations.

The log-likelihood becomes $l(\theta)=n_{u}\log(\theta)+(\sum x_{i}+3n_{c})\log(1-\theta)$ .

Differentiating, the score function is

S(\theta)=l^{\prime}(\theta)=\frac{n_{u}}{\theta}-\frac{\sum x_{i}+3n_{c}}{1-% \theta}.

A candidate MLE solves $l^{\prime}(\hat{\theta})=0$ , giving

	$\displaystyle\frac{n_{u}}{\hat{\theta}}$	$\displaystyle=\frac{\sum x_{i}+3n_{c}}{1-\hat{\theta}}$
	$\displaystyle n_{u}(1-\hat{\theta})$	$\displaystyle=\hat{\theta}\left(\sum x_{i}+3n_{c}\right)$
	$\displaystyle n_{u}$	$\displaystyle=\hat{\theta}\left(n_{u}+\sum x_{i}+3n_{c}\right)$
	$\displaystyle\hat{\theta}$	$\displaystyle=\frac{n_{u}}{n_{u}+\sum x_{i}+3n_{c}}.$

The value of the MLE using these data is $\frac{214}{214+102}=0.677$ .

Compare this to the original MLE of 0.682.

Why is the new estimate different to this?

Why is the difference small?

13.2 Suppression of Information

Last time we introduced the score function (the derivative of the log-likelihood), and the observed information function (MINUS the second derivative of the log-likelihood). The score function is zero at the MLE. The observed information function evaluated at the MLE gives us a method to construct confidence intervals.

We will now study the concept of observed information in more detail.

TheoremExample 13.2.1 Human Genotyping

Humans are a diploid species, which means you have two copies of every gene (one from your father, one from your mother). Genes occur in different forms; this is what leads to some of the different traits you see in humans (e.g. eye colour). Mendelian traits are a special kind of trait that are determined by a single gene.

Having wet or dry earwax is a Mendelian trait. Earwax wetness is controlled by the gene ABCC11 (this gene lives about half way along chromosome 16). We will call the wet earwax version of ABCC11 W, and the dry version w. The wet version is dominant, which means you only need one copy of W to have wet earwax. Both copies of the gene need to be w to get dry earwax.

The Hardy-Weinberg law of genetics states that if W occurs in a (randomly mating) population with proportion $p$ (so w occurs with proportion $(1-p)$ ) potential combinations in humans obey the proportions:

combination	WW	Ww	ww
proportion	$p^{2}$	$2p(1-p)$	$(1-p)^{2}$

Suppose I take a sample of 100 people and assess the wetness of their earwax. I observe that 87 of the people have wet earwax and 13 of them have dry earwax.

I am actually interested in $p$ , the proportion of copies of W in my population.

Show that the probability of a person having wet earwax is $p(2-p)$ , and that the probability of a person having dry earwax is $(1-p)^{2}$ . Also show that these two probabilities sum to $1$ .

The number of people with wet earwax in my sample is therefore $\operatorname{Binomial}(100,p(2-p))$ . So

{\color[rgb]{1,1,1}\Pr[\text{obs}|p]={100\choose 87}\left\{p(2-p)\right\}^{87}% \left\{(1-p)^{2}\right\}^{13}.}

IMPORTANT FACT: when writing down the likelihood, we can always omit multiplicative constants, since they become additive in the log-likelihood, then disappear in the differentation. A multiplicative constant is one that does not depend on the parameter of interest (here $p$ ).

So we can write down the likelihood as

	$\displaystyle L(p)$	$\displaystyle\propto\left\{p(2-p)\right\}^{87}\left\{(1-p)^{2}\right\}^{13}$
		$\displaystyle=\left\{p(2-p)\right\}^{87}(1-p)^{26}.$

So the log likelihood is

	$\displaystyle l(p)$	$\displaystyle=87\log\left\{p(2-p)\right\}+26\log(1-p)$
		$\displaystyle=87\log(p)+87\log(2-p)+26\log(1-p)$

(plus constant).

Now $p$ is a continuous parameter so a suitable way to find a candidate MLE is to differentiate. The score function is

{\color[rgb]{1,1,1}S(p)=l^{\prime}(p)=\frac{87}{p}-\frac{87}{2-p}-\frac{26}{1-% p}.}

We can solve $S(\hat{p})=0$ ; it is as a quadratic in $\hat{p}$ :

1

$87(2-p)(1-p)-87p(1-p)-26p(2-p)=0,$
2

$200\hat{p}^{2}-400\hat{p}+174=0,$
3

$\frac{400\pm\sqrt{400^{2}-4.200.174}}{2.200}=\hat{p}.$

This gives two solutions but we need $\hat{p}\in[0,1]$ as it is a proportion, so get $\hat{p}=0.639$ as our potential MLE.

The second derivative is

l^{\prime\prime}(p)=-\frac{87}{p^{2}}-\frac{87}{(2-p)^{2}}-\frac{26}{(1-p)^{2}}.

This is clearly $<0$ at $\hat{p}$ , confirming that it is a maximum.

The observed information is obtained by substituting $\hat{p}$ into $-l^{\prime\prime}(p)$ , giving

{\color[rgb]{1,1,1}I_{O}(\hat{p})=\frac{87}{0.639^{2}}+\frac{87}{(2-0.639)^{2}% }+\frac{26}{(1-0.639)^{2}}=459.5.}

Hence an approximate 95% confidence interval for $p_{\text{true}}$ is given by

	$\displaystyle(l,u)$	$\displaystyle=\left(\hat{p}-\frac{1.96}{\sqrt{I_{O}(\hat{p})}},\hat{p}+\frac{1% .96}{\sqrt{I_{O}(\hat{p})}}\right)$
		$\displaystyle={\color[rgb]{1,1,1}\left(0.639-\frac{1.96}{\sqrt{459.5}},0.639+% \frac{1.96}{\sqrt{459.5}}\right)}$
		$\displaystyle={\color[rgb]{1,1,1}(0.548,0.730)}.$

After all that derivation, don’t forget the context. This is a 95% confidence interval for the proportion of people with a W variant of ABCC11 gene in the population of interest.

Suppose that, instead of looking in people’s ears to see whether their wax is wet or dry we decide to genotype them instead, thereby knowing whether they are WW, Ww or ww.

This is a considerably more expensive option (although perhaps a little less disgusting) so a natural question is: what do we gain by doing this?

We take the same 100 people and find that 42 are WW, 45 are Ww and 13 are ww. Think about how this relates back to the earwax wetness. Did we need to genotype everyone?

The likelihood function for $p$ given our new information is

	$\displaystyle L(p)\propto$	$\displaystyle\ (p^{2})^{42}\left\{2p(1-p)\right\}^{45}\left\{(1-p)^{2}\right\}% ^{13}$
		$\displaystyle=\ p^{84}\left\{2p(1-p)\right\}^{45}(1-p)^{26}.$

The log-likelihood is

	$\displaystyle l(p)$	$\displaystyle=84\log(p)+45\log\left\{2p(1-p)\right\}+26\log(1-p)$
		$\displaystyle=84\log(p)+45\log(2)+45\log(p)+45\log(1-p)+26\log(1-p)$
		$\displaystyle=129\log(p)+71\log(1-p)+c.$

where $c$ is a constant.

As before, $p$ is continuous so we can find candidates for the MLE by differentiating:

{\color[rgb]{1,1,1}S(p)=l^{\prime}(p)=\frac{129}{p}-\frac{71}{1-p}.}

Now solving $S(\hat{p})=0$ gives a candidate MLE

1

$\frac{129}{\hat{p}}=\frac{71}{1-\hat{p}}$ ,
2

$129(1-\hat{p})=71\hat{p}$ ,

i.e.

\displaystyle\hat{p}=\frac{129}{200}=0.645.

This is our potential MLE. Checking the second derivative

l^{\prime\prime}(p)=-\frac{129}{p^{2}}-\frac{71}{(1-p)^{2}},

which is $<0$ at $\hat{p}$ confirming that it is a maximum.

The observed information is obtained by substituting $\hat{p}$ into $-l^{\prime\prime}(p)$ , giving

I_{O}(\hat{p})=\frac{129}{0.645^{2}}+\frac{71}{(1-0.645)^{2}}=873.5.

Hence an approximate 95% confidence interval for $p_{\text{true}}$ is given by

	$\displaystyle(l,u)$	$\displaystyle=\left(\hat{p}-\frac{1.96}{\sqrt{I_{O}(\hat{p})}},\hat{p}+\frac{1% .96}{\sqrt{I_{O}(\hat{p})}}\right)$
		$\displaystyle=\left(0.645-\frac{1.96}{\sqrt{873.5}},0.645+\frac{1.96}{\sqrt{87% 3.5}}\right)$
		$\displaystyle=(0.579,0.711).$

Now, compare the confidence intervals and the observed informations from the two separate calculations. What do you conclude?

Of course, genotyping the participants of the study is expensive, so may not be worthwhile. If this was a real problem, the statistician could communicate the figures above to the geneticist investigating gene ABCC11, who would then be able to make an evidence-based decision about how to conduct the experiment.

13.3 Sufficiency

Recall the driving test data from the Example 13.1.

Number of failed attempts	0	1	2	$\geq 3$
Observed frequency	147	47	20	5

Table 13.2: Number of times taken for drivers to pass the driving test.

We chose to model these data as being geometrically distributed. Assuming that the people in the ‘3 or more’ column failed exactly three times, the log-likelihood for general data $x_{1},\ldots,x_{n}$ is

	$\displaystyle l(\theta)$	$\displaystyle=\sum_{i=1}^{n}\log\left\{\theta(1-\theta)^{x_{i}}\right\}$
		$\displaystyle=\sum_{i=1}^{n}\{\log(\theta)+x_{i}\log(1-\theta)\}$
		$\displaystyle=n\log(\theta)+\log(1-\theta)\sum_{i=1}^{n}x_{i}.$

Now, suppose that, rather than being presented with the table of passing attempts, you were simply told that with 219 people filling in the survey, $\sum_{i=1}^{219}x_{i}=102$ .

Would it still be possible to proceed with fitting the model?

The answer is yes; moreover, we can proceed in exactly the same way, and achieve the same results! This is because, if you look at the log-likelihood, the only way in which the data is involved is through $\sum_{i=1}^{n}x_{i}$ , meaning that in some sense, this is all we need to know.

This is clearly a big advantage, we just have to remember one number rather than an entire table.

We call $\sum_{i=1}^{n}x_{i}$ a sufficient statistic for $\theta$ .

Definition.

Let ${\bf x}=x_{1},\ldots,x_{n}$ be a sample from $f(\cdot|\theta)$ . Then a function of the data $T({\bf x})$ is said to be a sufficient statistic for $\theta$ (or sufficient for $\theta$ ) if ${\bf x}$ is independent of $\theta$ given $T({\bf x})$ , i.e.

\Pr[{\bf X}={\bf x}|T({\bf x}),\theta]=\Pr[{\bf X}={\bf x}|T({\bf x})].

Some consequences of this definition:

1

For the objective of learning about $\theta$ , if I am told $T({\bf x})$ , there is no value in being told anything else about ${\bf x}$ .
2

If I have two datasets ${\bf x_{1}}$ and ${\bf x_{2}}$ , and $T({\bf x_{1}})=T({\bf x_{2}})$ , then I should make the same conclusions about $\theta$ from both, even if ${\bf x_{1}}\neq{\bf x_{2}}$ .
3

Sufficient statistics always exist since trivially $T({\bf x})={\bf x}$ always satisfies the above definition.

Definition.

Let ${\bf x}=x_{1},\ldots,x_{n}$ be a sample from $f(\cdot|\theta)$ . Let $T({\bf x})$ be sufficient for $\theta$ . Then $T({\bf x})$ is said to be minimally sufficient for $\theta$ if there is no sufficient statistic with a lower dimension than $T$ .

Theorem (Neyman factorisation theorem).

Let ${\bf x}=x_{1},\ldots,x_{n}$ be a sample from $f(\cdot|\theta)$ . Then a function $T({\bf x})$ is sufficient for $\theta$ if and only if the likelihood function can be factorised in the form

L(\theta)=g({\bf x})\times h(T({\bf x}),\theta),

where $g$ is a function of the data only, and $h$ is a function of the data only through $t({\bf x})$ .

For a proof see page 276 of Casella and Berger.

We can also express the factorisation result in terms of the log-likelihood, which is often easier, just by taking logs of the above result:

	$\displaystyle l(\theta)$	$\displaystyle=\log\big{\{}g({\bf x})\times h(T({\bf x}),\theta)\big{\}}$
		$\displaystyle=\log\{g({\bf x})\}+\log\{h(T({\bf x}),\theta)\}$
		$\displaystyle=\tilde{g}({\bf x})+\tilde{h}(T({\bf x}),\theta),$

where $\tilde{g}=\log(g)$ and $\tilde{h}=\log(h)$ .

We can show that $\sum_{i=1}^{n}x_{i}$ is sufficient for $\theta$ in the driving test example by inspection of the log-likelihood:

l(\theta)=n\log(\theta)+\log(1-\theta)\sum_{i=1}^{n}x_{i}.

Letting $T({\bf x})=\sum_{i=1}^{n}x_{i}\$ , then $\tilde{h}(T({\bf x}),\theta)=n\log(\theta)+\log(1-\theta)T({\bf x})$ , and $\tilde{g}({\bf x})=0$ , we have satisfied the factorisation criterion, and hence $T({\bf x})=\sum_{i=1}^{n}x_{i}$ is sufficient for $\theta$ .

Suppose that I carry out another survey on attempts to pass a driving test, again with $n=219$ participants and get data $\vec{y}=y_{1},\ldots,y_{n}$ , with ${\bf x}\neq{\bf y}$ but $\sum_{i=1}^{n}x_{i}=\sum_{i=1}^{n}y_{i}$ . Are the following statements true or false?

1

$\hat{\theta}({\bf x})$ , the MLE based on data ${\bf x}$ , is the same as $\hat{\theta}({\bf y})$ , the MLE based on data ${\bf y}$ .
2

The confidence intervals based on both datasets will be identical.
3

The geometric distribution is appropriate for both datasets.

An important shortcoming in only considering the sufficient statistic is that it does not allow us to check how well the chosen model fits.

TheoremExample 13.3.1 Poisson parameter (cont.)

Recall from the beginning of this section, the London homicides data, which we modelled as a random sample from the Poisson distribution. We found

	$\displaystyle L(\lambda\|x_{1},\ldots,x_{n})$	$\displaystyle=\prod_{i=1}^{n}\frac{\lambda^{x_{i}}\exp(-\lambda)}{x_{i}!}$
		$\displaystyle=\lambda^{\sum_{i}x_{i}}\exp(-n\lambda)\prod_{i=1}^{n}\frac{1}{x_% {i}!}$
		$\displaystyle\propto\lambda^{\sum_{i}x_{i}}\exp(-n\lambda),$

and that the log-likelihood function for the Poisson data is consequently

l(\lambda)=\log(\lambda)\sum_{i=1}^{n}x_{i}-n\lambda+c,

with the MLE being

\hat{\lambda}=\frac{\sum_{i=1}^{n}x_{i}}{n}=\bar{x}.

By differentiating again, we can find the information function

l^{\prime\prime}(\lambda|{\bf x})=-\lambda^{-2}\sum_{i=1}^{n}x_{i},

and so

I_{O}(\lambda|{\bf x})=\lambda^{-2}\sum_{i=1}^{n}x_{i}.

What is a sufficient statistic for the Poisson parameter?

For this case, we can let $T({\bf x})=\sum_{i=1}^{n}x_{i}\$ , and $\tilde{h}(T({\bf x}),\theta)=\log(\lambda)T({\bf x})-n\lambda$ , and $\tilde{g}({\bf x})=c=-\sum_{i=1}^{n}\log(x_{i}!)$ , we have satisfied the factorisation criterion, and hence $T({\bf x})=\sum_{i=1}^{n}x_{i}$ is sufficient for $\lambda$ .

TheoremExample 13.3.2 Normal variance

Suppose the sample $x_{1},\ldots,x_{n}$ comes from $X\sim N(0,\theta)$ . Find a sufficient statistic for $\theta$ . Is the MLE a function of this statistic or of the sample mean? Give a formula for the 95% confidence interval of $\theta$ .

First, the $\operatorname{Normal}(0,\theta)$ density is given by

\displaystyle{\color[rgb]{1,1,1}f(x_{i}|\theta)=\frac{1}{\sqrt{2\pi\theta}}% \exp\left\{-\frac{x_{i}^{2}}{2\theta}\right\},}

leading to the likelihood

1

${\color[rgb]{1,1,1}L(\theta)=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi\theta}}\exp% \left\{-\frac{x_{i}^{2}}{2\theta}\right\},}$
2

${\color[rgb]{1,1,1}L(\theta)=\frac{1}{\theta^{n/2}}\exp\left\{-\frac{\sum_{i}x% _{i}^{2}}{2\theta}\right\}.}$

Hence, $T({\bf x})=\sum_{i}x_{i}^{2}$ is a sufficient statistic for $\theta$ . The log-likelihood and score functions are

1

${\color[rgb]{1,1,1}l(\theta)=-\frac{n}{2}\log\theta-\frac{\sum_{i}x_{i}^{2}}{2% \theta},}$
2

${\color[rgb]{1,1,1}S(\theta)=l^{\prime}(\theta)=-\frac{n}{2\theta}+\frac{\sum_% {i}x_{i}^{2}}{2\theta^{2}}.}$

Solving $S(\theta)=0$ gives a candidate MLE

\displaystyle\hat{\theta}=\frac{\sum_{i}x_{i}^{2}}{n},

which is a function of the sufficient statistic. To check this is an MLE we calculate

\displaystyle l^{\prime\prime}(\theta)=\frac{n}{2\theta^{2}}-\frac{\sum_{i}x_{% i}^{2}}{\theta^{3}}.

In this case it isn’t immediately obvious that $l^{\prime\prime}(\hat{\theta})<0$ , but substituting in

	$\displaystyle l^{\prime\prime}(\hat{\theta})$	$\displaystyle=\frac{n}{2\left(\frac{\sum x_{i}^{2}}{n}\right)^{2}}-\frac{\sum x% _{i}^{2}}{\left(\frac{\sum x_{i}^{2}}{n}\right)^{3}}$
		$\displaystyle=\frac{n^{3}}{2(\sum x_{i}^{2})^{2}}-\frac{n^{3}}{(\sum x_{i}^{2}% )^{2}}$
		$\displaystyle=-\frac{n^{3}}{2(\sum x_{i}^{2})^{2}}<0,$

confirming that this is an MLE.

The observed information is $I_{O}(\hat{\theta})=-l^{\prime\prime}(\hat{\theta})$ ,

{\color[rgb]{1,1,1}I_{O}(\hat{\theta})=\frac{n^{3}}{2(\sum x_{i}^{2})^{2}}.}

Therefore a 95% confidence interval is given by

	$\displaystyle(l,u)$	$\displaystyle=\left(\hat{\theta}-\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}},\ % \hat{\theta}+\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}}\right)$
		$\displaystyle={\color[rgb]{1,1,1}\left(\frac{\sum_{i}x_{i}^{2}}{n}-1.96n^{-3/2% }\sum x_{i}^{2}\sqrt{2},\ \ \frac{\sum_{i}x_{i}^{2}}{n}+1.96n^{-3/2}\sum x_{i}% ^{2}\sqrt{2}\right)}.$

13.4 Summary

{mdframed}

1

The score function is the first derivative of the log-likelihood. The observed information is MINUS the second derivative of the log-likelihood. It will always be positive when evaluated at the MLE.

DO NOT FORGET THE MINUS SIGN!
2

The likelihood function adjusts appropriately when more information becomes available. Observed information does what it says. Higher observed information leads to narrower confidence intervals. This is a good thing as narrower confidence intervals mean we are more sure about where the true value lies.
For a continuous parameter of interest, $\theta$ , the calculation of the MLE and its confidence interval follows the steps:
1. 1
  
  Write down the likelihood, $L(\theta)$ .
2. 2
  
  Write down the log-likelihood, $l(\theta)$ .
3. 3
  
  Work out the score function, $S(\theta)=l^{\prime}(\theta)$ .
4. 4
  
  Solve $S(\hat{\theta})=0$ to get a candidate for the MLE, $\hat{\theta}$ .
5. 5
  
  Work out $l^{\prime\prime}(\theta)$ . Check it is negative at the MLE candidate to verify it is a maximum.
6. 6
  
  Work out the observed information, $I_{O}(\hat{\theta})=-l^{\prime\prime}(\theta)$ .
7. 7
  
  Calculate the confidence interval for $\theta_{\text{true}}$ :
  
  $\left(\hat{\theta}-\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}},\hat{\theta}+\frac{% 1.96}{\sqrt{I_{O}(\hat{\theta})}}\right).$
3

Changing the data that your inference is based on will change the amount of information, and subsequent inference (e.g. confidence intervals).
4

A statistic $T({\bf x})$ is said to be sufficient for a parameter $\theta$ , if ${\bf x}$ is independent of $\theta$ when conditioning on $S({\bf x})$ .
5

An equivalent, and easier to demonstrate condition is that the likelihood can be factorised in the form $L(\theta)=g({\bf x})\times h(T({\bf x}),\theta)$ , iff $T({\bf x})$ is sufficient.

Chapter 14 Distribution of the MLE

14.1 Recalling randomness

We have noted that an asymptotic 95% confidence interval for a true parameter, $\theta$ , is given by

{\color[rgb]{1,1,1}\left(\hat{\theta}-\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}},% \hat{\theta}+\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}}\right),}

where $\hat{\theta}$ is the MLE and

{\color[rgb]{1,1,1}I_{O}(\theta|{\bf x})=-l^{\prime\prime}(\theta|{\bf x})=-% \frac{\partial^{2}}{\partial\theta^{2}}l(\theta|{\bf x}),}

is the observed information.

In this lecture we will sketch the derivation of the distribution of the MLE, and show why the above really is an asymptotic 95% confidence interval for $\theta$ .

Recall the distinction between an estimate and an estimator.

Given a sample $X_{1},\ldots,X_{n}$ , an estimator is any function $W(X_{1},\ldots,X_{n})$ of that sample. An estimate is a particular numerical value produced by the estimator for given data $x_{1},\ldots,x_{n}$ .

The maximum likelihood estimator is a random variable; therefore it has a distribution. A maximum likelihood estimate is just a number, based on fixed data.

For the rest of this lecture we consider an iid sample $X_{1},\ldots,X_{n}$ , from some distribution with unknown parameter $\theta$ , and the MLE (maximum likelihood estimator) $\hat{\theta}({\bf X})$ .

Definition.

The Fisher information of a random sample $X_{1},\ldots,X_{n}$ is the expected value of minus the second derivative of the log-likelihood, evaluated at the true value of the parameter:

I_{E}(\theta)=\mathbb{E}\left[-\frac{\partial^{2}}{\partial\theta^{2}}l(\theta% |{\bf X})\right].

This is related to, but different from, the observed information.

1

The observed information is calculated based on observed data; the Fisher information is calculated taking expectations over random data.
2

The observed information is calculated at $\hat{\theta}$ , the Fisher information is calculated at $\theta_{\text{true}}$ .
3

The observed information can be written down numerically; the Fisher information usually cannot be since it depends on $\theta_{\text{true}}$ , which is unknown.

TheoremExample 14.1.1 Fisher Information for a Poisson parameter

Suppose ${\bf x}$ is a random sample from $X\sim\operatorname{Poisson}(\theta_{\text{true}})$ . Find the Fisher information. Remember that $\mathbb{E}[X]=\theta_{\text{true}}$ . For $\theta>0$ ,

	$\displaystyle L(\theta)=f({\bf x}\|\theta)$	$\displaystyle=\prod_{i=1}^{n}\frac{e^{-\theta}\theta^{x_{i}}}{x_{i}!}$
		$\displaystyle=e^{-n\theta}\theta^{\sum_{i}x_{i}}\times c$

where $c$ is a constant.

1

$\log f({\bf x}|\theta)={\color[rgb]{1,1,1}-n\theta+\sum_{i}x_{i}\log\theta+c},$
2

$\frac{\partial}{\partial\theta}\log f({\bf x}|\theta)={\color[rgb]{1,1,1}\frac% {\sum_{i}x_{i}}{\theta}-n,}$
3

$\frac{\partial^{2}}{\partial\theta^{2}}\log f({\bf x}|\theta)={\color[rgb]{% 1,1,1}\frac{-\sum_{i}x_{i}}{\theta^{2}},}$
4

$\frac{\partial^{2}}{\partial\theta^{2}}\log f({\bf X}|\theta)={\color[rgb]{% 1,1,1}\frac{-\sum_{i}X_{i}}{\theta^{2}}.}$

Hence

	$\displaystyle I_{E}(\theta_{\text{true}})$	$\displaystyle=\mathbb{E}\left(\frac{\sum_{i}X_{i}}{\theta_{\text{true}}^{2}}\right)$
		$\displaystyle=\frac{n\theta_{\text{true}}}{\theta_{\text{true}}^{2}}=\frac{n}{% \theta_{\text{true}}}.$

We see that our answer is in terms of $\theta_{\text{true}}$ , which is unknown (and not in terms of the data!) The Fisher information is useful for many things in likelihood inference, to see more take MATH330 Likelihood Inference.

Here, it features in the most important theorem in the course.

Theorem (Asymptotic distribution of the maximum likelihood estimator).

Suppose we have an iid sample ${\bf X}=X_{1},\ldots,X_{n}$ from some distribution with unknown parameter $\theta$ , with maximum likelihood estimator $\hat{\theta}({\bf X})$ . Then (under certain regularity conditions) in the limit as $n\rightarrow\infty$

\hat{\theta}({\bf X})\sim\operatorname{N}\left(\theta,I_{E}^{-1}(\theta)\right).

This says that, for $n$ large, the distribution of the MLE is approximately normal with mean equal to the true value of the parameter, and variance equal to the reciprocal of the Fisher information.

We will not prove the result in this course, but it has to do with the central limit theorem (from MATH230).

Turning this around, this means that, for large $n$ ,

\Pr\left[\theta\in\left(\hat{\theta}({\bf X})-1.96\sqrt{I_{E}^{-1}(\theta)},% \hat{\theta}({\bf X})-1.96\sqrt{I_{E}^{-1}(\theta)}\right)\right]\approx 0.95.

This result is useless as it stands, because we can only calculate $I_{E}(\theta)$ when we know $\theta$ , and if we know it, why are we constructing a confidence interval for it?!

Luckily, the result also works asymptotically if we replace $I_{E}(\theta)$ by $I_{O}(\hat{\theta})$ , giving that

\left(\hat{\theta}({\bf x})-\frac{1.96}{\sqrt{I_{O}(\hat{\theta}({\bf x}))}},% \hat{\theta}({\bf x})+\frac{1.96}{\sqrt{I_{O}(\hat{\theta}({\bf x}))}}\right)

is an approximate 95% confidence interval for $\theta$ (as claimed earlier).

Exam Question

A large batch of electrical components contains a proportion $\theta$ which are defective and not repairable, a proportion $3\theta$ which are defective but repairable and a proportion $1-4\theta$ which are satisfactory.

(a)

What values of $\theta$ are admissible?

Fifty components are selected at random (with replacement) from the batch, of which 2 are defective and not repairable, 5 are defective and repairable and 43 are satisfactory.

(b)

Write down the likelihood function, $L(\theta)$ and make a rough sketch of it.
(c)

Obtain the maximum likelihood estimate of $\theta$ .
(d)

Obtain an approximate 95% confidence interval for $\theta$ . A value of $\theta$ equal to 0.02 is believed to represent acceptable quality for the batch. Do the data support the conclusion that the batch is of acceptable quality?

Solution:

a
There are 3 types of component, each giving rise to a constraint on $\theta$ :
1. 1
  
  $0\leq\theta\leq 1$ ,
2. 2
  
  $0\leq 3\theta\leq 1$ ,
3. 3
  
  $0\leq 1-4\theta\leq 1$ ,
as the components each need to have valid probabilities. The third inequality is sufficient for the other two and gives $0\leq\theta\leq 1/4$ .
b

Given the data, the likelihood is

$\displaystyle L(\theta)$ $\displaystyle\propto\theta^{2}(3\theta)^{5}(1-4\theta)^{43}$

$\displaystyle\propto\theta^{7}(1-4\theta)^{43}.$

For the sketch note that $L(0)=L(1/4)=0$ and the function is concave and positive between these two with a maximum closer to $0$ than $1/4$ .
c

To work out the MLE, we differentiate the (log-)likelihood as usual. The log-likelihood is

$l(\theta)=7\log\theta+43\log(1-4\theta).$

Differentiating,

$l^{\prime}(\theta)=\frac{7}{\theta}-\frac{4\times 43}{1-4\theta}.$

A candidate MLE solves $l^{\prime}(\hat{\theta})=0$ , giving $\hat{\theta}=\frac{7}{200}$ .

Moreover,

$l^{\prime\prime}(\theta)=-\frac{7}{\theta^{2}}-\frac{4\times 4\times 43}{(1-4% \theta)^{2}}<0,$

so this is indeed the MLE.
d

The observed information is

$\displaystyle I_{O}(\hat{\theta})$ $\displaystyle=-l^{\prime\prime}(\hat{\theta})$

$\displaystyle=\frac{7}{\hat{\theta}^{2}}+\frac{4\times 4\times 43}{(1-4\hat{% \theta})^{2}}$

$\displaystyle=5714.3+930.2$

$\displaystyle=6644.5.$

So a $95\%$ confidence interval for $\theta$ is

$\left(\hat{\theta}-\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}},\hat{\theta}+\frac{% 1.96}{\sqrt{I_{O}(\hat{\theta})}}\right)$

$=(0.0110,0.0590).$

As $0.02$ is within this confidence interval there is no evidence of this batch being sub-standard.

14.2 Summary

{mdframed}

1

Under certain regularity conditions, the maximum likelihood estimator has, asymptotically, a normal distribution with mean equal to the true parameter value, and variance equal to the inverse of the Fisher information.
2

The Fisher information is minus the expectation of the second derivative of the log-likelihood evaluated at the true parameter value.
3

Based on this, we can construct approximate 95% confidence intervals for the true parameter value based on the MLE and the observed information.
4

Importantly, this is an asymptotic result so is only approximate. In particular, it is a bad approximation to a 95% confidence interval when the sample size, $n$ , is small.

Chapter 15 Deviance and the LRT

15.1 Deviance-based confidence intervals

In the last lecture we showed that the MLE is asymptotically normally distributed, and we use this fact to construct an approximate 95% confidence interval.

In this lecture we will introduce the concept of deviance, and show that this leads to another way to calculate approximate confidence intervals that have various advantages.

We will begin by showing through an example where things can go wrong with the confidence intervals we know (and love?).

TheoremExample 15.1.1 An evening at the casino

On a fair (European) roulette wheel there is a $1/37$ probability of each number coming up.

In the early 1990s, Gonzalo Garcia-Pelayo believed that casino roulette wheels were not perfectly random, and that by recording the results and analysing them with a computer, he could gain an edge on the house by predicting that certain numbers were more likely to occur next than the odds offered by the house suggested. This he did at the Casino de Madrid in Madrid, Spain, winning 600,000 euros in a single day, and one million euros in total.

Legal action against him by the casino was unsuccessful, it being ruled that the casino should fix its wheel:

http://en.wikipedia.org/wiki/Roulette#Biased_wheels

Suppose I am curious that the number 17 seems to come up on a casino’s roulette wheel more frequently than other numbers. I track it for 30 spins, during which it comes up 2 times. I decide to carry out a likelihood analysis on $p$ , the probability of the number 17 coming up, and its confidence interval.

We propose to model the situation as follows. Let $R$ be the number of times the number 17 comes up in 30 spins of the roulette wheel. We decide to model $R\sim\operatorname{Binomial}(30,p)$ .

Why is this a suitable model?

What assumptions are being made?

Are these assumptions reasonable?

The probability of the observed data is given by

{\color[rgb]{1,1,1}\Pr[\text{obs}|p]={30\choose 2}p^{2}(1-p)^{28}.}

The likelihood is simply the probability of the observed data, but we can ignore the multiplicative constants, so

{\color[rgb]{1,1,1}L(p)\propto p^{2}(1-p)^{28}.}

The log-likelihood is

l(p)=2\log p+28\log(1-p).

Differentiating,

{\color[rgb]{1,1,1}l^{\prime}(p)=\frac{2}{p}-\frac{28}{1-p}.}

Now remember solutions to $l^{\prime}(p)=0$ are potential MLEs:

1

${\color[rgb]{1,1,1}\frac{2}{\hat{p}}=\frac{28}{1-\hat{p}},}$
2

${\color[rgb]{1,1,1}2-2\hat{p}=28\hat{p},}$
3

${\color[rgb]{1,1,1}\hat{p}=\frac{2}{30}.}$

The second derivative will both tell us whether this is a maximum, and provide the observed information:

l^{\prime\prime}(p)=-\frac{2}{p^{2}}-\frac{28}{(1-p)^{2}}.

This is clearly negative for all $p\in(0,1)$ , so $\hat{p}$ must be a maximum.

Moreover, the observed information is

	$\displaystyle I_{O}(\hat{p})=-l^{\prime\prime}(\hat{p})$	$\displaystyle=\frac{2}{\hat{p}^{2}}+\frac{28}{(1-\hat{p})^{2}}$
		$\displaystyle=450+32.413$
		$\displaystyle=482.143.$

A 95% confidence interval for $p$ is given by

\left(\hat{p}-\frac{1.96}{\sqrt{I_{O}(\hat{p})}},\hat{p}+\frac{1.96}{\sqrt{I_{% O}(\hat{p})}}\right),

which, on substituting in $\hat{p}$ and the observed information becomes

\left(\frac{2}{30}-\frac{1.96}{\sqrt{482.143}},\frac{2}{30}+\frac{1.96}{\sqrt{% 482.143}}\right)=(-0.023,0.156).

The resulting confidence interval includes negative values (for a probability parameter). What’s the problem??

Let’s look at a plot of the log-likelihood for the above situation.

⬇

loglik<-function(p){

2*log(p) + 28*log(1-p)

}

p<-seq(from=0.01,to=0.25,length=1000)

plot(p,loglik(p),type="l")

We notice that the log-likelihood is quite asymmetric. This happens because the MLE is close to the edge of the feasible space (i.e. close to 0). The confidence interval defined above is forced to be symmetric, which seems inappropriate here.

Definition.

Suppose we have a log-likelihood function with unknown parameter $\theta$ , $l(\theta)$ . Then the deviance function is given by

D(\theta)=2\big{\{}l(\hat{\theta})-l(\theta)\big{\}}.

Notice that $D(\theta)\geq 0$ , and $D(\hat{\theta})=0$ .

What can we say about $D(\theta)$ ?

This is a fixed (but unknown) value for fixed data ${\bf x}=x_{1},\ldots,x_{n}$ . However, in similar spirit to the last lecture, we can consider random data ${\bf X}=X_{1},\ldots,X_{n}$ . Now, the deviance function depends on ${\bf X}$ (since different data leads to different likelihoods). So, $D(\theta,{\bf X})$ is a random variable.

Theorem 2 (Asymptotic distribution of the deviance).

Suppose we have an iid sample ${\bf X}=X_{1},\ldots,X_{n}$ from some distribution with unknown parameter $\theta$ . Then (under certain regularity conditions) in the limit as $n\rightarrow\infty$ ,

D(\theta,{\bf X})\sim\chi^{2}_{1},

i.e. the deviance of the true value of $\theta$ has a $\chi^{2}$ distribution with one degree of freedom.

The practical upshot of this result is that we have another way to construct a confidence interval for $\theta$ . A 95% confidence interval for $\theta$ , for example, is given by ${\color[rgb]{1,1,1}\{\theta:D(\theta)<3.84\}}$ , i.e. any values of $\theta$ whose deviance is smaller than 3.84.

TheoremExample 15.1.2 An evening at the casino continued

This property of the deviance is best seen visually. Going back to the roulette data:

⬇

deviance<-function(p){

2*(loglik(2/30)-loglik(p))

}

plot(p,deviance(p),type="l")

abline(h=3.84)

From the graph we can estimate the confidence interval based on the deviance. In fact the exact answer to three decimal places is $(0.011,0.192)$ . Notice that this is not symmetrical, and that all values in the interval are feasible.

The original motivation for all of this was that we were wondering if the number 17 comes up more often than with the 1/37 that should be observed in a fair roulette wheel.

In fact 1/37=0.027, which is within the 95% confidence interval calculated above. Hence there is insufficient evidence (so far) to support the claim that this number is coming up more often than it should.

Notes (summary)

1

We have now seen two different ways to calculate approximate confidence intervals (CI) for an unknown parameter. Previously, we calculated CI based on the asymptotic distribution of the MLE (CI-MLE). Here, we showed how to calculate the CI based on the asymptotic distribution of the deviance (CI-D).
2

We discussed various differences and pros and cons of the two:
1. 1
  
  CI-MLE is always symmetric about the MLE. CI-D is not.
2. 2
  
  CI-MLE can include values with zero likelihood (e.g. infeasible values such as negative probabilities, as seen here). CI-D will only include feasible values.
3. 3
  
  CI-D is typically harder to calculate than CI-MLE.
4. 4
  
  For reasons we will not go into here, CI-D is typically more accurate than CI-MLE.
5. 5
  
  CI-D is invariant to re-parametrization; CI-MLE is not. (This is a good thing for CI-D, that we will learn more about in subsequent lectures).
3

Overall, CI-D is usually preferred to CI-MLE (since the only disadvantage is that it is harder to compute).
4

DEVIANCES ARE ALWAYS NON-NEGATIVE!

15.2 Re-parametrization and Invariance

TheoremExample 15.2.1 Accident and Emergency continued

In our likelihood examples we discussed modelling inter-arrival times at an A&E department using an Exponential distribution. The exponential pdf is given by

f(x)=\lambda\exp(-\lambda x)

for $x\geq 0$ and $\lambda\geq 0$ , where $\lambda$ is the rate parameter.

Based on the inter-arrival times (in minutes):

18.39,2.70,5.42,0.99,5.42,31.97,2.96,5.28,8.51,10.90,

giving $\bar{x}=9.259$ , we came up with the MLE for $\lambda$ of $\hat{\lambda}=\frac{1}{\bar{x}}=0.108$ .

Now, $\mathbb{E}[X]=\mu=1/\lambda$ .

How would we go about finding an estimate for $\mu$ ?

Method 1: re-write the pdf as

{\color[rgb]{1,1,1}f(x)=\frac{1}{\mu}\exp\left(-\frac{x}{\mu}\right),}

where $x\geq 0$ and $\mu\geq 0$ , to give a likelihood of

{\color[rgb]{1,1,1}L(\mu)=\prod_{i=1}^{n}\frac{1}{\mu}\exp\left(-\frac{x_{i}}{% \mu}\right),}

then find the MLE by the usual approach.

Method 2: Since $\mu=1/\lambda$ , presumably $\hat{\mu}=1/\hat{\lambda}=1/0.108=9.259$ .

Which method is more convenient?

Which method appears more rigorous?

In fact, both methods give the same solution always. This property is called invariance to reparameterization of the MLE. It is a nice property both because it agrees with our intuition, and saves us a lot of potential calculation.

Theorem (Invariance of MLE to reparametrisation.).

If $\hat{\theta}$ is the MLE of $\theta$ and $\phi$ is a monotonic function of $\theta$ , $\phi=g(\theta)$ , then the MLE of $\phi$ is $\hat{\phi}=g(\hat{\theta})$ .

Proof.

Write ${\bf x}=(x_{1},x_{2},\dots,x_{n})$ . The likelihood for $\theta$ is $L(\theta)=f(\vec{x}|\theta)$ , and for $\phi$ is $L_{\phi}(\phi)$ . Note that $\theta=g^{-1}(\phi)$ as $g$ is monotonic and define $\hat{\phi}$ by $g(\hat{\theta})$ . To show that $\hat{\phi}$ is the MLE,

	$\displaystyle L_{\phi}(\phi)$	$\displaystyle=f({\bf x}\|\phi)$
		$\displaystyle=f({\bf x}\|g^{-1}(\phi))\leq f({\bf x}\|\hat{\theta})$

as $\hat{\theta}$ is MLE. But

	$\displaystyle f({\bf x}\|\hat{\theta})$	$\displaystyle=f({\bf x}\|g^{-1}(\hat{\phi}))$
		$\displaystyle=f({\bf x}\|\hat{\phi})=L_{\phi}(\hat{\phi}).$

∎

This means that both methods above must give the same answer.

Exercise.

Show this works for the case above, by demonstrating that Method 1 leads to $\hat{\mu}=\bar{x}=9.259$ .

The following corollary follows immediately from invariance of the MLE to reparametrisation.

Corollary.

Confidence intervals based on the deviance are invariant to reparametrisation, in the sense that

\{\phi:D(g^{-1}(\phi))\leq 3.84\}=\{\theta:D(\theta)\leq 3.84\}.

Proof.

	$\displaystyle\{\theta:D(\theta)\leq 3.84\}$	$\displaystyle={\color[rgb]{1,1,1}\{\theta:2(l(\hat{\theta})-l(\theta))\leq 3.8% 4\}}$
		$\displaystyle=\{\phi:2(l(g^{-1}(\hat{\phi}))-l(g^{-1}(\phi)))\leq 3.84\}$

by Theorem above, which equals

\displaystyle{\color[rgb]{1,1,1}\{\phi:D(g^{-1}(\phi))\leq 3.84\}.}

∎

The practical consequence of this is that if

$(\theta_{l},\theta_{u})$ is a deviance confidence interval with coverage $p$ for $\theta_{\text{true}}$ ,

then

$(g(\theta_{l}),g(\theta_{u}))$ is a deviance confidence interval with coverage $p$ for $\phi_{\text{true}}$ .

(Of course, $\phi=g(\theta)$ ).

IMPORTANT: This simple translation does not hold for confidence intervals based on the asymptotic distribution to the MLE. This is because that depends on the second derivative of $l(\cdot)$ with respect to the parameter, which will be different in more complicated ways for different parameter choices.

This will be explored more in MATH330 Likelihood Inference.

Exam Question

a

The random variables $X_{1},X_{2},\ldots,X_{n}$ are independent and identically distributed with the geometric distribution

$f(x|\theta)=\theta^{x}(1-\theta),\ x=0,1,2,\ldots$

where $\theta$ is a parameter in the range of $0\leq\theta\leq 1$ to be estimated. The mean of the above geometric distribution is $\theta/(1-\theta)$ .
1. i
  
  Write down formulae for the maximum likelihood estimator for $\theta$ and for Fisher’s information;
2. ii
  
  Write down what you know about the distribution of the maximum likelihood estimator for this example when $n$ is large.
b

In a particular experiment, $n=10$ , $\sum_{i=1}^{n}x_{i}=10$ .
1. i
  
  Compute an approximate 95% confidence interval for $\theta$ based on the asymptotic distribution of the maximum likelihood estimator;
2. ii
  
  Compute the deviance $D(\theta)$ and sketch it over the range $0.1\leq\theta\leq 0.9$ . Use your sketch to describe how to use the deviance to obtain an approximate 95% confidence interval for $\theta$ ;
3. iii
  
  If you were asked to produce an approximate 95% confidence interval for the mean of the distribution $\theta/(1-\theta)$ , what would be your recommended approach? Justify your answer.

Solution:

a
1. i
  
  For the model, the likelihood function is
  
  $\displaystyle L(\theta|{\bf X})$ $\displaystyle=\prod_{i=1}^{n}\theta^{X_{i}}(1-\theta)$
  
  $\displaystyle=(1-\theta)^{n}\theta^{\sum X_{i}}.$
  
  The log-likelihood is then
  
  $l(\theta|{\bf X})=n\log(1-\theta)+\sum X_{i}\log(\theta),$
  
  with derivative
  
  $l^{\prime}(\theta|{\bf X})=-\frac{n}{1-\theta}+\frac{\sum X_{i}}{\theta}.$
  
  A candidate MLE solves $l^{\prime}(\hat{\theta})=0$ , giving
  
  $\hat{\theta}=\frac{\sum X_{i}}{n+\sum X_{i}}.$
  
  Moreover,
  
  $l^{\prime\prime}(\theta|{\bf X})=-\frac{n}{(1-\theta)^{2}}-\frac{\sum X_{i}}{% \theta^{2}}<0,$
  
  so this is indeed the MLE.
  
  For the Fisher Information,
  
  $\displaystyle I_{E}(\theta)$ $\displaystyle=\mathbb{E}\left[-l^{\prime\prime}(\theta|{\bf X})|_{\theta=% \theta}\right]$
  
  $\displaystyle=\mathbb{E}\left[\frac{n}{(1-\theta)^{2}}-\frac{\sum X_{i}}{% \theta^{2}}\right]$
  
  $\displaystyle=\frac{n}{(1-\theta)^{2}}+\frac{n}{\theta^{2}}\mathbb{E}[X_{1}]$
  
  $\displaystyle=\frac{n}{\theta_{\text{true}}(1-\theta)^{2}},$
  
  after simplification, since $\mathbb{E}[X_{1}]=\theta/(1-\theta)$ .
2. ii
  
  Using the Fisher information, the asymptotic distribution of the MLE is
  
  $\hat{\theta}({\bf X})\sim N(\theta_{\text{true}},I_{E}^{-1}(\theta_{\text{true% }}))\approx N(\theta_{\text{true}},I_{0}^{-1}(\hat{\theta})).$
b
1. i
  
  Using the data, the MLE is $\hat{\theta}=\frac{10}{10+10}=\frac{1}{2}$ . The observed information is
  
  $I_{O}(\hat{\theta})=\frac{10}{(1-1/2)^{2}}+\frac{10}{(1/2)^{2}}=80.$
  
  Therefore a $95\%$ confidence interval is
  
  $(1/2-\frac{1.96}{\sqrt{80}},1/2+\frac{1.96}{\sqrt{80}})=(0.281,0.719).$
2. ii
  
  The deviance is given by
  
  $\displaystyle D(\theta)$ $\displaystyle=2\{l(\hat{\theta})-l(\theta)\}$
  
  $\displaystyle=2\{10\log(1/2)+10\log(1/2)-10\log(1-\theta)-10\log(\theta)\}$
  
  $\displaystyle=20\left(-2\log 2-\log(\theta(1-\theta))\right).$
  
  To plot the deviance calculate $D(0.1)$ and $D(0.9)$ , and note that $D(0.5)=D(\hat{\theta})=0$ . A $95\%$ confidence interval is obtained by drawing a horizontal line at 3.84; the interval is all $\theta$ with $D(\theta)\leq 3.84$ .
3. iii
  
  To construct a confidence interval for the mean, we would use the mean function on the deviance-based confidence interval just calculated, as this is invariant to re-parametrization.

15.3 Summary

{mdframed}

1

The simple, intuitive answer is true: if $\hat{\theta}$ is a MLE, then if $\phi=g(\theta)$ for any monotonic transformation $g$ , then $\hat{\phi}=g(\hat{\theta})$ .
2

The same simple result can be applied to confidence intervals based on the deviance, but can NOT be applied to confidence intervals based on the asymptotic distribution of the MLE.

	$\displaystyle L(\theta)$	$\displaystyle\propto\theta^{2}(3\theta)^{5}(1-4\theta)^{43}$
		$\displaystyle\propto\theta^{7}(1-4\theta)^{43}.$

	$\displaystyle I_{O}(\hat{\theta})$	$\displaystyle=-l^{\prime\prime}(\hat{\theta})$
		$\displaystyle=\frac{7}{\hat{\theta}^{2}}+\frac{4\times 4\times 43}{(1-4\hat{% \theta})^{2}}$
		$\displaystyle=5714.3+930.2$
		$\displaystyle=6644.5.$

	$\displaystyle L(\theta\|{\bf X})$	$\displaystyle=\prod_{i=1}^{n}\theta^{X_{i}}(1-\theta)$
		$\displaystyle=(1-\theta)^{n}\theta^{\sum X_{i}}.$

	$\displaystyle I_{E}(\theta)$	$\displaystyle=\mathbb{E}\left[-l^{\prime\prime}(\theta\|{\bf X})\|_{\theta=% \theta}\right]$
		$\displaystyle=\mathbb{E}\left[\frac{n}{(1-\theta)^{2}}-\frac{\sum X_{i}}{% \theta^{2}}\right]$
		$\displaystyle=\frac{n}{(1-\theta)^{2}}+\frac{n}{\theta^{2}}\mathbb{E}[X_{1}]$
		$\displaystyle=\frac{n}{\theta_{\text{true}}(1-\theta)^{2}},$

	$\displaystyle D(\theta)$	$\displaystyle=2\{l(\hat{\theta})-l(\theta)\}$
		$\displaystyle=2\{10\log(1/2)+10\log(1/2)-10\log(1-\theta)-10\log(\theta)\}$
		$\displaystyle=20\left(-2\log 2-\log(\theta(1-\theta))\right).$