XIV Central potentials
The isotropic harmonic oscillator is an example of a spherical symmetric potential, where the potential energy only depends on the radial distance from the origin, . These potentials are called central potentials. Another example is the Coulomb potential
| (235) |
of two charges and . For central potentials the Schrödinger equation
| (236) |
can also be separated in three one-dimensional problems, but only when one works in spherical polar coordinates. Note: Here mass is denoted by the symbol since we need later for a different purpose.
XIV.1 Spherical polar coordinates
The three spherical coordinates are the radial coordinate , the azimuthal angle , and the polar angle .
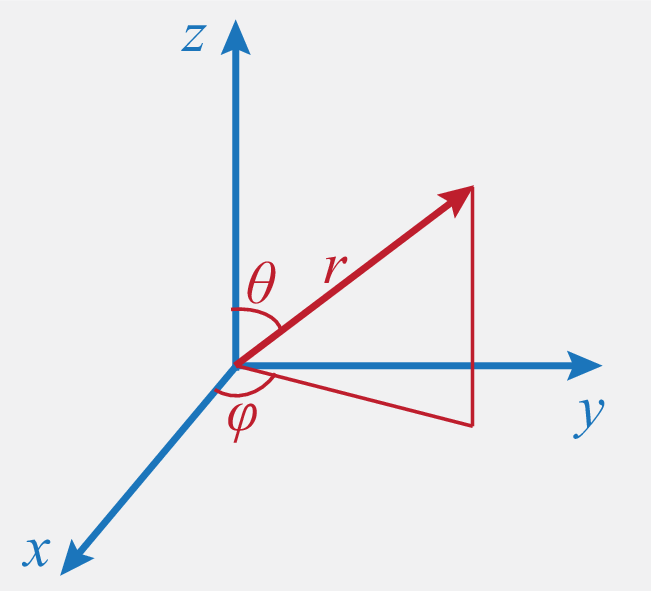
The cartesian coordinates can be written as
| (237) | |||||
| (238) | |||||
| (239) |
The Laplace operator is given by
| (240) |
We abbreviate the angular part as
| (241) |
XIV.2 Separation of variables in spherical polar coordinates
We separate the radial dependence from the angular dependence in the wavefunction, . From the Schrödinger equation (236) one finds that the angular part solves the equation , i.e.,
| (242) |
while the radial part solves the equation
| (243) |
where is a constant.
XIV.3 Angular part
Since Eq. (242) for the angular part does not depend on the potential we can solve this equation once and for all. The solutions are the spherical harmonics
| (244) |
for , for .
Here is called the azimuthal quantum number and is called the magnetic quantum number. Note that for each there are values of .
For the functions are the Legendre polynomials
| (245) |
Hence
| (246) | |||||
| (247) | |||||
| (248) | |||||
| (249) |
For the functions are the associated Legendre polynomials
| (250) |
The first spherical harmonics are
| (251) | |||||
| (252) | |||||
| (253) | |||||
| (254) | |||||
| (255) | |||||
| (256) |
XIV.4 Quantisation of angular momentum
The angular momentum operator is given by , hence etc. The squared length is given by . One can show that
| (257) |
| (258) |
Hence the spherical harmonics are eigenfunctions of and , with eigenvalues and , respectively.
XIV.5 Degeneracy of the radial part
Equation (243) for the radial part depends on the potential and hence has to be solved separately for every problem in order to find the energies . However, since this equation only depends on the azimuthal quantum number but not on the magnetic quantum number , each energy level is at least fold degenerate, since for each there are solutions of the angular equation with different values of .