Home page for accesible maths 6 Linear transformations 6.2 Linear transformations versus matrices 6.4 Transformations of the Euclidean space,

{\mathbb{R}}^{3}

Style control - access keys in brackets

Font (2 3) - + Letter spacing (4 5) - + Word spacing (6 7) - + Line spacing (8 9) - +

6.3. Invertible linear transformations

Definition 6.3.1.

A linear transformation $T$ is invertible (also called non-singular) if there is another linear transformation ${T}^{-1}$ such that $T{T}^{-1}={T}^{-1}T=\operatorname{Id}\nolimits.$ Here $\operatorname{Id}\nolimits$ denotes the identity transformation $\operatorname{Id}\nolimits(x)=x$ . Then ${T}^{-1}$ is called the inverse of $T$ . If $T$ does not have an inverse, then it is called non-invertible.

Example 6.3.2.

Rotations and reflections are invertible linear transformations of the plane. The inverse operation of rotation by $\theta$ is rotation by $-\theta$ . And a reflection composed with itself is the identity. Thus

${R}^{-1}_{\theta}=R_{2\pi-\theta}\quad\hbox{and}\quad{H}^{-1}_{\theta}=H_{% \theta}.$

Theorem 6.3.3.

Let $T:{\mathbb{R}}^{n}\to{\mathbb{R}}^{n}$ be a linear transformation, and let $A$ be its associated matrix. Then

T

is invertible if and only if

A

is invertible.

In this case, ${A}^{-1}$ is the matrix associated to the inverse ${T}^{-1}$ of $T$ .

Proof.

By assumption, $T(v)=Av$ for all $v\in{\mathbb{R}}^{n}$ . Suppose that $T$ is invertible and let $B$ be the matrix associated to ${T}^{-1}$ . Then for each $v\in{\mathbb{R}}^{n}$ we have

v=\left\{\begin{array}[]{l}T{T}^{-1}(v)=ABv\\ {T}^{-1}T(v)=BAv\end{array}\right.

It follows from the Proposition 1.4.9 that $AB=BA=I_{n}$ . That is, $A$ is invertible and $B={A}^{-1}$ as required.

Conversely, if $A$ is invertible, we observe that ${A}^{-1}$ is the matrix associated to the linear transformation $S$ which satisfies $ST=TS=\operatorname{Id}\nolimits$ , that is, we must have that $S={T}^{-1}$ and $T$ is invertible. ∎

Recall that a square matrix is invertible if and only if its determinant is non-zero (Theorem 4.4.4).

Example 6.3.4.

Find the inverse of $T(x,y)=(x+y,x-y)$ .
Solution 1: This is the linear transformation associated to the matrix $A=\begin{pmatrix}1&1\\ 1&-1\end{pmatrix}$ . We know $T$ is invertible since $\det A=-2\neq 0$ . The inverse of $T$ is the linear transformation given by the matrix ${A}^{-1}$ , by Theorem 6.3.3. We calculate the inverse as follows:

$(A|I_{2})\xrightarrow{R_{2}=r_{2}-r_{1}}\left(\begin{array}[]{rr|rr}1&1&1&0\\ 0&-2&-1&1\end{array}\right)\xrightarrow{\begin{array}[]{l}R_{2}=-\frac{1}{2}r_% {2}\\ R_{1}=r_{1}-r_{2}\end{array}}{\left(\begin{array}[]{rr|rr}1&0&\frac{1}{2}&% \frac{1}{2}\\ 0&1&\frac{1}{2}&-\frac{1}{2}\end{array}\right)},$

and therefore

${A}^{-1}=\frac{1}{2}\begin{pmatrix}1&1\\ 1&-1\end{pmatrix}.$

Hence ${T}^{-1}(x,y)=\frac{1}{2}(x+y,x-y)$ .
Solution 2: One could also solve this example without matrices as follows. We have $T$ invertible if and only if there exists a linear map ${T}^{-1}~{}:~{}{\mathbb{R}}^{2}\to{\mathbb{R}}^{2}$ such that

${T}^{-1}T(xe_{1}+ye_{2})=T{T}^{-1}(xe_{1}+ye_{2})=xe_{1}+ye_{2}\quad\hbox{for % all $x,y\in{\mathbb{R}}$.}\quad$

Now, if $T(xe_{1}+ye_{2})=ae_{1}+be_{2}$ , then ${T}^{-1}(ae_{1}+be_{2})=xe_{1}+ye_{2}$ . So we can use the following equations to solve for $x, y$ in terms of $a, b$ :

$a=x+y\quad\hbox{and}\quad b=x-y\quad\hbox{give}\quad x=\frac{a+b}{2}\quad\hbox% {and}\quad y=\frac{a-b}{2}.$

Therefore, ${T}^{-1}(ae_{1}+be_{2})=\frac{a+b}{2}e_{1}+\frac{a-b}{2}e_{2}$ for all $a,b\in{\mathbb{R}}$ . In other words, ${T}^{-1}(x,y)=\frac{1}{2}(x+y,x-y)$ .

Theorem 6.3.5.

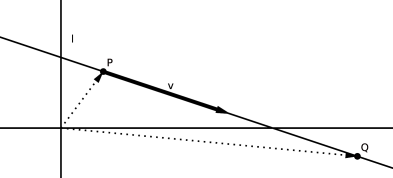
Invertible linear transformations of the plane preserve lines. That is, given an invertible linear transformation $T$ of ${\mathbb{R}}^{2}$ and $l$ a line in ${\mathbb{R}}^{2}$ , then the image under $T$ of the points of $l$ form a line $l^{\prime}$ , and conversely, each point of $l^{\prime}$ is the image under $T$ of exactly one point of $l$ .

Proof.

A line $l$ in ${\mathbb{R}}^{2}$ is given by a point $P=(p_{1},p_{2})$ and a non-zero direction vector $v=\begin{pmatrix}v_{1}\\ v_{2}\end{pmatrix}$ . In other words, a point $Q=(q_{1},q_{2})$ is on $l$ if and only if there exists some $\lambda\in{\mathbb{R}}$ such that $Q=P+\lambda v$ ; in matrix form

\begin{pmatrix}q_{1}\\ q_{2}\end{pmatrix}=\begin{pmatrix}p_{1}\\ p_{2}\end{pmatrix}+\lambda\begin{pmatrix}v_{1}\\ v_{2}\end{pmatrix}=\begin{pmatrix}p_{1}+\lambda v_{1}\\ p_{2}+\lambda v_{2}\end{pmatrix}\quad\hbox{(see Figure~{}\ref{fig:paramline}).}\quad

Figure 5. Parametrisation of the line $l$ by $P$ and $v$ . The scalar $\lambda$ of Theorem 6.3.5 is defined as the real number such that $Q-P=\lambda v$

Now, by linearity of $T$ we have

T\begin{pmatrix}p_{1}+\lambda v_{1}\\ p_{2}+\lambda v_{2}\end{pmatrix}=T\begin{pmatrix}p_{1}\\ p_{2}\end{pmatrix}+\lambda T\begin{pmatrix}v_{1}\\ v_{2}\end{pmatrix}=T(P)+\lambda T(v).

Since $T$ is invertible, $T(v)\neq 0$ , and therefore $T(P+\lambda v)$ lies on the line through the point $T(P)$ which has direction vector $T(v)$ . Hence, the image of $l$ under $T$ is a line. Since $T$ is invertible, the inverse ${T}^{-1}$ of $T$ maps the line $T(l)$ to $l$ , saying that there is a bijective correspondence between the points of $l$ and those of $T(l)$ . ∎

Remark 6.3.6.

If $T$ is non-invertible in Theorem 6.3.5, then the result is not true. For example, the zero map, which maps all points to the zero vector, is linear but not invertible. It clearly does not map lines to other lines. As another example, consider the projection $\pi_{1}$ onto the $x$ -axis, which is the linear transformation corresponding to the matrix $\begin{pmatrix}1&0\\ 0&0\end{pmatrix}$ . The line $~{}l~{}:~{}x=0$ , i.e. the $y$ -axis, is mapped to the zero vector by $\pi_{1}$ , and in particular it is not mapped to a line.

Example 6.3.7.

Consider the line in the plane ${\mathbb{R}}^{2}$ given by the equation

$l~{}:~{}y=2x+3\quad\hbox{and let}\quad A=\begin{pmatrix}-1&2\\ 2&0\end{pmatrix}.$

Since $\det A=-4\neq 0$ , the linear transformation $T:{\mathbb{R}}^{2}\to{\mathbb{R}}^{2}$ corresponding to $A$ is invertible. Find the image $l^{\prime}=T(l)$ of the line $l$ by $T$ .
Solution 1: First let’s write the line in the form: $P+\lambda v$ , for $\lambda\in{\mathbb{R}}$ . Let $P=(0,3)$ , which clearly lies on $l$ . One checks that if $v=(1,2)$ , then the line $l$ is the set of points $P+\lambda v$ , for $\lambda\in{\mathbb{R}}$ . Therefore the new line is

$l^{\prime}\;:\;T(P+\lambda v)=T(P)+\lambda T(v)=\begin{pmatrix}6\\ 0\end{pmatrix}+\lambda\begin{pmatrix}3\\ 2\end{pmatrix},\quad\hbox{for $\lambda\in{\mathbb{R}}.$}\quad$

Solution 2: Any line is uniquely determined by two of its points. Thus, to find the image of $l$ , we pick two distinct points $P$ and $Q$ on $l$ , calculate their images $P^{\prime}$ and $Q^{\prime}$ by $T$ and write the equation of the line $l^{\prime}$ as the line going through $P^{\prime}$ and $Q^{\prime}$ . Let us choose

$P=(0,3)\quad\hbox{and}\quad Q=(-1,1).$

Note that $P, Q$ are indeed on $l$ since they both satisfy the equation $y=2x+3$ . We then calculate

$P^{\prime}=T(0,3)=(6,0)\quad\hbox{ and }\quad Q^{\prime}=T(-1,1)=(3,-2).$

So the line going through $P^{\prime}$ and $Q^{\prime}$ has equation:

$\frac{y-0}{x-6}=\frac{-2-0}{3-6}=\frac{2}{3}\quad\hbox{ which is the same as }% \quad l^{\prime}~{}:~{}y=\frac{2}{3}x-4.$