Home page for accesible maths 6 Linear transformations 6 Linear transformations 6.2 Linear transformations versus matrices

Style control - access keys in brackets

Font (2 3) - + Letter spacing (4 5) - + Word spacing (6 7) - + Line spacing (8 9) - +

6.1. Definition and first examples

Definition 6.1.1.

We will use the word transformation to refer to any function $T$ from ${\mathbb{R}}^{n}$ to ${\mathbb{R}}^{m}$ . We will write

T~{}:~{}{\mathbb{R}}^{n}\longrightarrow{\mathbb{R}}^{m}.

So if $v\in{\mathbb{R}}^{n}$ then $T(v)\in{\mathbb{R}}^{m}$ . In this case we call $T(v)$ the image of $v$ .

Definition 6.1.2.

A transformation $T:{\mathbb{R}}^{n}\to{\mathbb{R}}^{m}$ is called a linear transformation if $T$ satisfies the two axioms

LT1

$T(v+w)=T(v)+T(w)$ for all $v,w\in{\mathbb{R}}^{n}$ , and
LT2

$T(\lambda v)=\lambda T(v)$ for all $\lambda\in{\mathbb{R}}$ and all $v\in{\mathbb{R}}^{n}$ .

Recall Definition 1.2.1, which says that for $\lambda\in{\mathbb{R}}$ , the vector $\lambda v$ is obtained by multiplying each coordinate by $\lambda$ .

Example 6.1.3.

The following transformations $T:{\mathbb{R}}\to{\mathbb{R}}$ are linear transformations:

$T(x)=2x,\quad T(x)=x,\quad T(x)=0.$

The following transformations $T:{\mathbb{R}}\to{\mathbb{R}}$ are not linear:

$T(x)=x+1,\quad T(x)=-2,\quad T(x)=\sin x,\quad T(x)=x^{2}.$

Remark 6.1.4.

If $T$ is linear, then $T(0+0)=T(0)+T(0)$ . Therefore, $T(0)=0$ .

Example 6.1.5.

Let $A\in\operatorname{M}_{{2}}({{\mathbb{R}}})$ , and consider the transformation $T:{\mathbb{R}}^{2}\to{\mathbb{R}}^{2}$ given by $T(v)=Av$ for each $v\in{\mathbb{R}}^{2}$ . Since $v$ is a column vector, the matrix product $A v$ is also a column vector. $T$ defined in this way is a linear transformation. This follows from Lemma 1.4.10. In particular, LT1 is satisfied, because $A(v+w)=Av+Aw$ , and LT2 is satisfied because $A(\lambda v)=\lambda(Av)$ for any $\lambda\in{\mathbb{R}}$ . So $T$ is called the linear transformation associated to the matrix $A$ .

The fundamental result of this section is that all linear transformations come from matrices, in the sense of Example 6.1. Before we make this statement more precise, let’s introduce some of the standard transformations. We will focus on three main types of transformations of ${\mathbb{R}}^{2}$ : translation, rotation, and reflection. Translation is not a linear transformation (by 6.1.4), but rotation and reflection are.

Definition 6.1.6.

Translation by a vector. This is an example of a transformation which is not linear. Given a vector $v=\begin{pmatrix}a\\ b\end{pmatrix}\in{\mathbb{R}}^{2}$ , the translation by $v$ is the transformation given by adding $v$ to every vector $z\in{\mathbb{R}}^{2}$ (See Figure 1). In other words, $T(z):=z+v$ . It may be written in coordinates as follows:

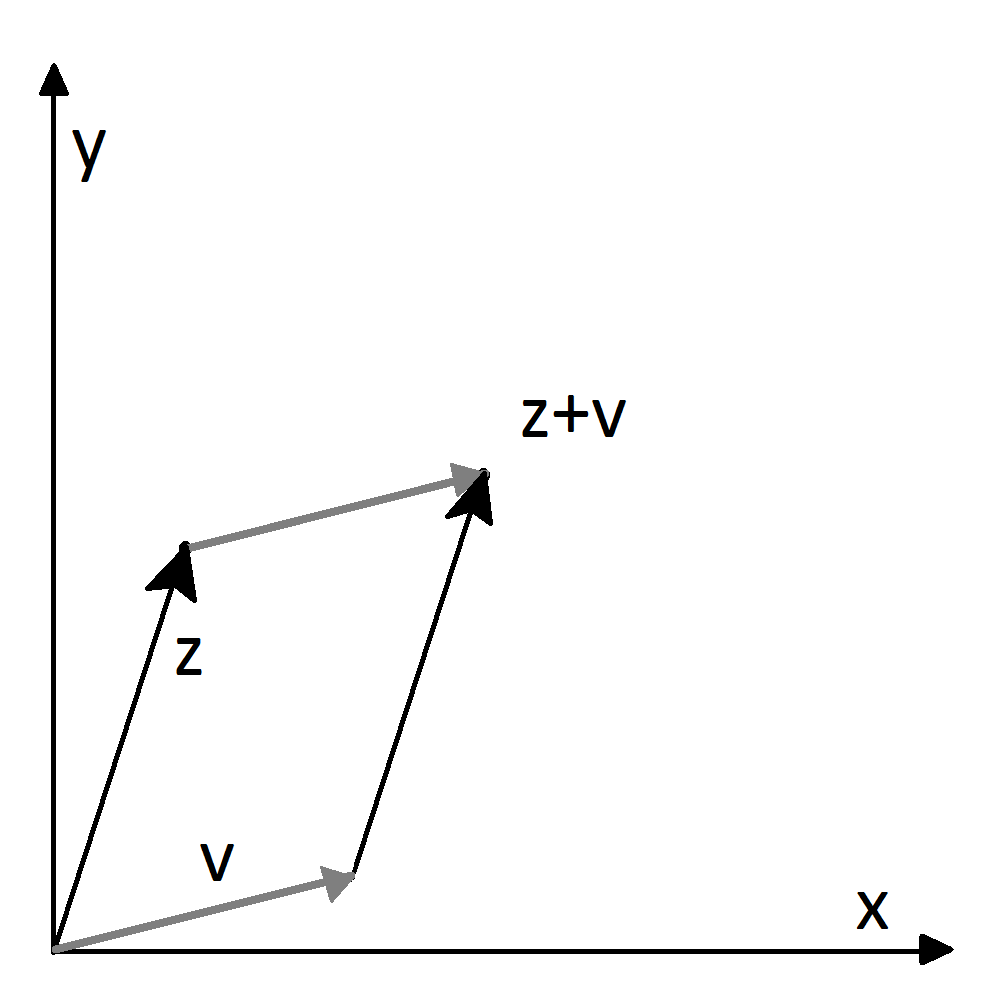
T_{v}(x,y)=(x+a,y+b)\quad\hbox{for all}\quad(x,y)\in{\mathbb{R}}^{2}.

Figure 1. The vector $z+v$ is the translation of $z$ by $v$ .

Definition 6.1.7.

Rotation by an angle. Given an angle $\theta\in[0,2\pi)$ (in radians), the rotation through $\theta$ is the anticlockwise rotation $R_{\theta}$ through $\theta$ about the origin (see Figure 2).

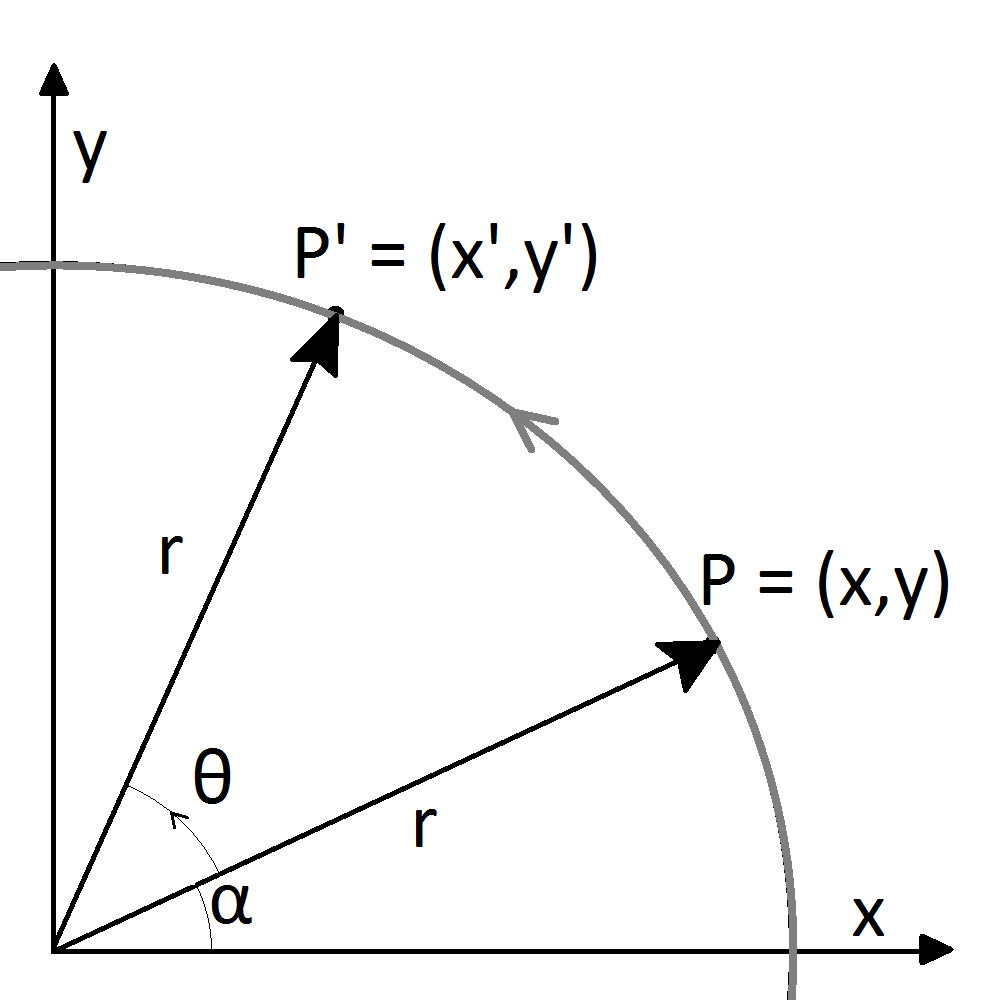
Figure 2. The point $P$ is mapped to the point $P^{\prime}$ by the rotation by angle $\theta$ around the origin $(0,0)$ . The vector corresponding to $P$ makes an angle $\alpha$ with the $x$ -axis.

Rotation around the origin is the linear transformation associated to the following matrix (in the sense of Example 6.1):

R_{\theta}=\begin{pmatrix}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta\end{pmatrix}.

For the proof of this fact, see Proposition 6.2.8.

Example 6.1.8.

1. (a)
  
  When $\theta=0$ , then nothing is rotated, so the transformation should be the identity transformation. Indeed:
  
  $R_{0}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}\cos 0&-\sin 0\\ \sin 0&\cos 0\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}x+0y\\ 0x+y\end{pmatrix}=\begin{pmatrix}x\\ y\end{pmatrix}\quad\hbox{for all}\quad\begin{pmatrix}x\\ y\end{pmatrix}\in{\mathbb{R}}^{2}.$
  
  In other words, $R_{0}=I_{2}$ .
2. (b)
  
  When $\theta=\pi$ , rotation by the angle $\pi$ should be the same as negating every vector. Indeed:
  
  $R_{\pi}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}\cos\pi&-\sin\pi\\ \sin\pi&\cos\pi\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}-x\\ -y\end{pmatrix}\quad\hbox{for all}\quad\begin{pmatrix}x\\ y\end{pmatrix}\in{\mathbb{R}}^{2}.$

Definition 6.1.9.

Reflection about a line. Given a line $l$ through the origin which makes an angle $\theta$ above the positive $x$ -axis, the reflection about $l$ is the transformation $H_{\theta}$ mapping any point $(x,y)\in{\mathbb{R}}^{2}$ to its reflection, assuming the line $l$ is a mirror.

Figure 3. The point $P^{\prime}$ is the image of $P$ by the reflection about the line $l$ . The line $l$ makes the angle $\theta$ with the $x$ -axis.

Reflection about a line through the origin is the linear transformation associated to the following matrix (in the sense of Example 6.1):

H_{\theta}=\begin{pmatrix}\cos 2\theta&\sin 2\theta\\ \sin 2\theta&-\cos 2\theta\end{pmatrix}.

For the proof of this fact, see Proposition 6.2.9.

Example 6.1.10.

1. (a)
  
  When $\theta=0$ , the reflecting line is the $x$ -axis, so we have
  
  $H_{0}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}\cos 0&\sin 0\\ \sin 0&-\cos 0\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}x+0y\\ 0x-y\end{pmatrix}=\begin{pmatrix}x\\ -y\end{pmatrix}\quad\hbox{for all}\quad\begin{pmatrix}x\\ y\end{pmatrix}\in{\mathbb{R}}^{2}.$
  
  This makes sense, because a reflection in the $x$ -axis should simply multiply the $y$ -coordinate by $-1$ .
2. (b)
  
  When $\theta=\frac{\pi}{2}$ , the reflecting line is the $y$ -axis, and we have
  
  $H_{\frac{\pi}{2}}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}\cos\pi&\sin\pi\\ \sin\pi&-\cos\pi\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}-x\\ y\end{pmatrix}\quad\hbox{for all}\quad\begin{pmatrix}x\\ y\end{pmatrix}\in{\mathbb{R}}^{2};$
  
  again, this is as one would expect.