Home page for accesible maths 6.3 Probability Density Function Recap of definite integrals 6.4 Expectation and variance

Style control - access keys in brackets

Font (2 3) - + Letter spacing (4 5) - + Word spacing (6 7) - + Line spacing (8 9) - +

The probability density function

Recall (page 4.3) that the CDF, $F_{R}(r)$ , of a discrete random variable, $R$ , is the sum of all of the relevant probabilities, $\sum_{i=-\infty}^{r}p_{R}(i)$ .

Analogously the (probability) density function, pdf, $f_{X}(x)$ , of a continuous random variable, $X$ , is defined as

f_{X}(x)=\frac{d}{dx}F_{X}(x),

so that it satisfies

F_{X}(x)=\int_{-\infty}^{x}f_{X}(s)\,ds.

(6.1)

For example

P(X\leq 10)=F_{X}(10)={\color[rgb]{1,1,1}\int_{-\infty}^{10}f_{X}(s)\,ds.}

Note that $s$ is a dummy variable; one could use any letter for the integrand except $x$ .

Figure 6.3: The probability density function corresponding to the cdf shown in Figure 6.2.

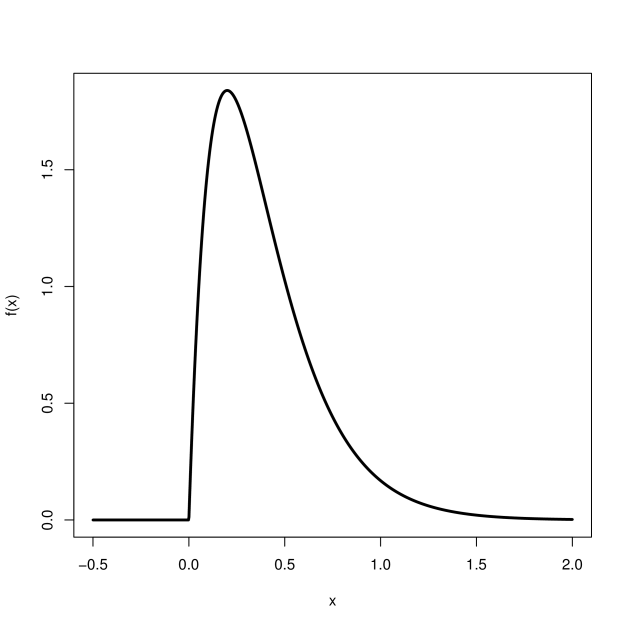
Figure 6.3 shows the pdf for the continuous random variable for which the cdf is shown in Figure 6.2. Notice that the pdf is zero in regions where there are no outcomes, in this example for $x\leq 0$ . Note also that it exceeds $1$ in some places, so it cannot be interpreted as a probability despite some of the mathematical properties of $f_{X}(x)$ that we shall see below being very similar to those of the probability mass function.

Properties of $f_{X}(x)$ :

1.

Positivity: $f_{X}(x)\geq 0$ for all $x$ , Why?
2.

Unit-integrability: $\int_{-\infty}^{\infty}f_{X}(x)\,dx=1$ . Why?

Consider the probability that an observation on a continuous random variable $X$ lies in the interval $(a,b]$ :

$\displaystyle{\rm P}(a<X\leq b)$	$\displaystyle=$	$\displaystyle{\rm P}(X\leq b)-{\rm P}(X\leq a)$
	$\displaystyle=$	$\displaystyle F_{X}(b)-F_{X}(a)$
	$\displaystyle=$	$\displaystyle\int_{-\infty}^{b}f_{X}(x)\,dx-\int_{-\infty}^{a}f_{X}(x)\,dx$
	$\displaystyle=$	$\displaystyle\int_{a}^{b}f_{X}(x)\,dx.$

We see that ${\rm P}(a<X\leq b)$ may be calculated as the area under the curve of $f_{X}(x)$ between $x=a$ and $x=b$ .

An illuminating idea

For some very small interval width $\delta$ ,

	$\displaystyle{\rm P}(x<X\leq x+\delta)$	$\displaystyle=$	$\displaystyle\int_{x}^{x+\delta}f_{X}(s)ds$
		$\displaystyle\approx$	$\displaystyle f_{X}(x)\delta.$

Thus $f_{X}(x)\delta$ can be thought of as (approximately) the probability that $X$ is between $x$ and $x+\delta$ .
Compare this with the interpretation (definition!) of the pmf $p_{R}(r)$ .

Exercise 6.2.

A random variable $X$ has cumulative distribution function

\displaystyle F_{X}(x)=\left\{\begin{array}[]{ll}1-\exp(-3x)&\mbox{ for }x\geq 0% ,\\ 0&\mbox{ for }x<0.\end{array}\right.

Find the pdf of $X$ .

Solution.

\displaystyle f_{X}(x)=\frac{\ d}{dx}F_{X}(x)=\left\{\begin{array}[]{ll}{% \color[rgb]{1,1,1}{3\exp(-3x)}}&{\color[rgb]{1,1,1}{\mbox{for }x\geq 0,}}\\ &\\ {\color[rgb]{1,1,1}{0}}&{\color[rgb]{1,1,1}{\mbox{for }x<0}}.\end{array}\right.

Example 6.3.

A triangular pdf: a random variable $X$ has pdf

f_{X}(x)=\left\{\begin{array}[]{ll}2(1-x)&0\leq x\leq 1,\\ 0&\mbox{otherwise}.\end{array}\right.

Obtain the cdf $F_{X}(x)$ .
Important: We split the range of $x$ , $(-\infty,\infty)$ into sensible intervals.

•

For $x\in(-\infty,0]$ ,

$F_{X}(x)=\int_{-\infty}^{x}f_{X}(s)\,{\rm d}s={\color[rgb]{1,1,1}{\int_{-% \infty}^{x}0\,{\rm d}s=0.}}$
•

For $x\in{{\color[rgb]{1,1,1}{(}}0,1]}$ ,

$\displaystyle F_{X}(x)$ $\displaystyle=$ $\displaystyle\int_{-\infty}^{x}f_{X}(s)\,{\rm d}s$

$\displaystyle=$ $\displaystyle F_{X}(0)+\int_{0}^{x}2(1-s)\,{\rm d}s$

$\displaystyle=$ $\displaystyle 0+\left[2s-s^{2}\right]_{0}^{x}$

$\displaystyle=$ $\displaystyle 2x-x^{2}$
•

For $x\in{(1,\infty)}$ ,

$F_{X}(x)=\int_{-\infty}^{x}f_{X}(s)\,{\rm d}s={\color[rgb]{1,1,1}F_{X}(1)+\int% _{1}^{x}0\,{\rm d}s=1.}$

Hence

F_{X}(x)=\left\{\begin{array}[]{ll}0&\quad\mbox{ for }\quad x\leq 0\\ 2x-x^{2}&\quad\mbox{ for }\quad 0<x\leq 1\\ 1&\quad\mbox{ for }\quad x>1.\end{array}\right.

Now find ${\rm P}(X<0.5)$ , ${\rm P}(0.5<X<0.8)$ and ${\rm P}(0.5<X<1.75)$ .

$\displaystyle F(0.5)$	$\displaystyle=$	$\displaystyle 2(0.5)-(0.5)^{2}=0.75$
$\displaystyle F(0.8)-F(0.5)$	$\displaystyle=$	$\displaystyle 2(0.8)-(0.8)^{2}-0.75=1.6-0.64-0.75=0.21$
$\displaystyle F(1.75)-F(0.5)$	$\displaystyle=$	$\displaystyle 1-0.75=0.25.$

Obtain ${\rm P}(0.5<X<0.8)$ directly from the pdf.

	$\displaystyle{\rm P}(0.5<X<0.8)$	$\displaystyle=$	$\displaystyle\int_{0.5}^{0.8}f_{X}(s)~{}ds=\int_{0.5}^{0.8}2(1-s)~{}ds=\left[2% s-s^{2}\right]_{0.5}^{0.8}$
		$\displaystyle=$	$\displaystyle 2(0.8)-(0.8)^{2}-2(0.5)+(0.5)^{2}=0.21$

Example 6.4.

The lifetime in years, that a computer functions before breaking down is a continuous random variable $X$ with pdf, given by

f_{X}(x)=\left\{\begin{array}[]{ll}\lambda\exp(-\lambda x)&x\geq 0,\\ 0&x<0.\end{array}\right.

The parameter $\lambda$ depends on the type of computer. To set a time for a guarantee the company wants to know the time $t$ for which with probability $0.9$ the lifetime of the computer will exceed $t$ .

Solution.

$\displaystyle{\rm P}(X>t)$	$\displaystyle=$	$\displaystyle\int_{t}^{\infty}f_{X}(x)\,dx$
	$\displaystyle=$	$\displaystyle\int_{t}^{\infty}\lambda\exp(-\lambda x)\,dx$
	$\displaystyle=$	$\displaystyle[-\exp(-\lambda x)]_{t}^{\infty}=\exp(-\lambda t),$

so that ${\rm P}(X>t)=0.9$ implies $t=-\lambda^{-1}\log(0.9)$ .

Note that you have just found a quantile of the distribution; see Section 6.4.1.

$\displaystyle F_{X}(x)$	$\displaystyle=$	$\displaystyle\int_{-\infty}^{x}f_{X}(s)\,{\rm d}s$
	$\displaystyle=$	$\displaystyle F_{X}(0)+\int_{0}^{x}2(1-s)\,{\rm d}s$
	$\displaystyle=$	$\displaystyle 0+\left[2s-s^{2}\right]_{0}^{x}$
	$\displaystyle=$	$\displaystyle 2x-x^{2}$

Style control - access keys in brackets

The probability density function

Properties of fX⁢(x):

An illuminating idea

Exercise 6.2.

Solution.

Example 6.3.

Example 6.4.

Solution.

Properties of $f_{X}(x)$ :