6.1 Introduction to Continuous Variables

Discrete random variables described the outcomes of experiments which were in a countable set (usually integer values). This covered models for the number of heads in a fixed number of tosses of a coin, the number of floods of a river in a year, the number of children in a family until a girl is born.

Focusing only on discrete random variables is too restrictive for many situations. Examples include the nicotine levels in the blood plasma of smokers, the time intervals between floods of a river, and the waiting time for admissions to an intensive care unit. In each case the outcome of the “experiment” is a measurement on a continuous scale. This suggests we need to consider continuous random variables, where a continuous random variable is a variable whose set of possible values is uncountable.

To describe continuous random variables we need slightly different mathematical tools than we used for discrete random variables. For example for a discrete random variable $R$ we used the probability mass function $p_R(r)=\mathrm{P}(R=r)$. However, if $X$ is a continuous random variable $\mathrm{P}(X=x)=0$ for all $x$. We focus on probabilities of events instead of probabilities of single outcomes. In particular we focus on events of the form

$$\{X\le x\}$$

for fixed $x$, and consider these as $x$ varies. For discrete random variables we defined (on page 4.3) the cumulative distribution function

$$F_R(r)=\mathrm{P}(R\le r)$$

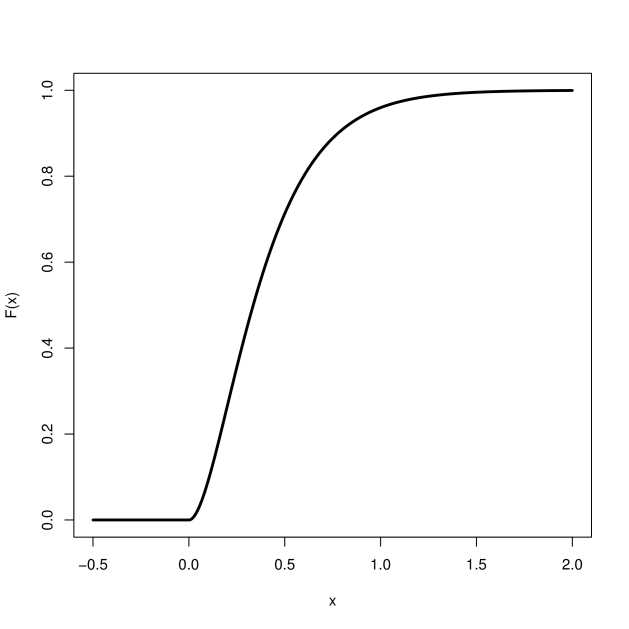
for discrete values $r$. This can equally well be defined for a continuous value $x$:

$$F_R(x)=\mathrm{P}(R\le x)=\mathrm{P}(R\le \lfloor x\rfloor )$$

where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$.

Figure 6.1 shows this function for a Poisson random variable $R$ with $\lambda =2$.

As $x$ varies the function $\mathrm{P}(R\le x)$ jumps at the integers where $R$ has probability.