|
|
|
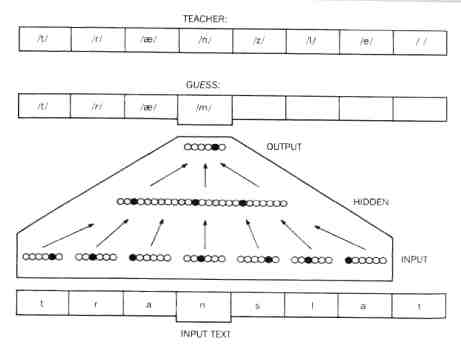 |
| Diagram of connectionist net: thanks to Churchland & Sejnowski, in the Reader, 2nd edition, p.142 |
A short clear authoritative account is here, thanks to Stanford University.
Churchland and Sejnowski have a picture of the way in which the net learns. (p.143) The crucial thing is the rule, given to the system, which alters the weighting of the connections in response to the outcome of a trial. You input a bit of a word and a noise is output. The formula calculates a measure of the difference between actual output and desired output (the correct pronunciation). It then alters the weightings of the connections in an arbitrary direction and another run is launched. A measure of the error is taken for this run. If the error is increased, the direction of reweighting tried the first time is reversed and a new run made. If this lowers the error (as it must?) weights are adjusted again in the same direction and another run made.
This iterative process, run many times, results in weightings which move the system towards the desired output. It may not be a smooth movement, but it will be movement that has the desired result in the long run.
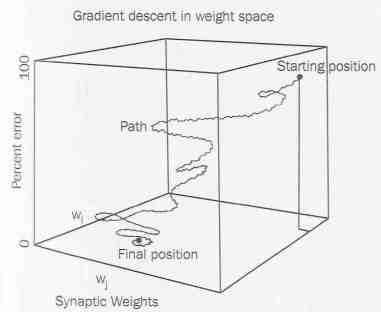 |
| From the Reader, p. 143. |
There is an indefinitely large number of possible weightings for the system. As the actual weightings are adjusted in the light of the result of each run, you can think of them tracing a path through 'weight space'. You can graph the error produced by any particular weighting against the weighting that produced it. Over time, the error is reduced until eventually it hits zero.
What is happening here is that a deterministic system is being got to 'pursuing a goal'.
There is a famous strategy for getting a system to pursue a goal (or to simulate pursuing a goal?) which is much simpler than the formula governing the changing of weightings in netTalk, and so might be clearer to understand.
It's the hill-climbing strategy, designed to get a system to reach the summit of a hill.
The rule is:
Measure your distance from the summit.
PROMPT: Would this be successful? Suggestion
Think of netTalk. Coded on the input layer are bits of written words - 'sh' for example, or 't'. The output layer is read as coding for sounds, eg 'sh' and 't' (read these as sounds!). Imagine it has been fully trained and then think of it enlarged and comprehensive. You then have a machine which reads input text.
You could then describe the situation as one which the system knows how to pronounce English words. It incorporates a bit - an important bit - of knowledge. We can therefore ask: how is the knowledge represented in the system?
(Remember that no rules are given to the system. There is no von Neumann-type programming.)
'...the network had to create new, internal representations in the hidden layer of processing units. How did the network organise its "knowledge"?'
Churchland and Sejnowski p.143.
I want to leave the question there. It seems a question that does arise. The point is made that connectionist systems represent knowledge, but not at all in the way von Neumann systems do. Churchland and Sejnowski sketch first goes at answers in their paper.
Somehow, nets are good at generalizing. This is just an empirical fact. If you teach it to recognize a squiggle, it will classify squiggles that look to us (i.e. are recognized by us as) 'similar' to the one it learnt from as similar. So they are used in classificatory and recognition tasks.
For example you can train a net to distinguish male from female faces.
For each training sequence you have put into the input layer a face and a code for male or female, whichever applies. When the net has learnt the gender of the one face, you present it with another - and so on. What you find is that if you give it enough training it will subsequently classify new faces on its own.
Prompt: What do you make of this? Magic?
Connectionism encourages a break with the analysis into methodological levels which the von Neumann model lends itself to.
The von Neumann model suggests: problem analysis, computational algorithm, implementation. On this view, 'computational problems could be analysed independent of an understanding of the algorithm that executes the computation, and the algorithmic problem could be solved independent of an understanding of the physical implementation.' Churchland and Sejnowski, Reader p.150.
This leads to the strategy of thinking of these as separate and separable aspects of the overall problem of working out how the brain works. You can work on elucidating the functions that need performing independently of working out the programming code that would get those functions performed, and you can work out the programming code required to perform the identified functions without knowing anything about the hardware it would have to run on - provided you thought about platform independent code.
This means in effect that you can work on functional analysis, and on how to programme the required functionality without knowing anything about the actual structure of the brain.
This is a bad strategy, because there are always many many different ways of programming a solution to the problem of performing a given function, ("computational space is very large") and to make good use of our time we need to concentrate on solutions which would be efficient given the actual computing resources that the system would have available - i.e. the brain. Though connectionist nets and von Neumann computers maybe logically equivalent - or at any rate von Neumann machines can do everything nets can do - one may be enormously more efficient at particular problems than the other, and vice versa. Hardware matters in other words to efficiency if not logical capacity.
This is a plea for interdisciplinarity, and in particular to the relevance of neuroscience to the question of simulating human capacities, to understanding how the brain performs its functions as well as its structure.
Reciprocally, neuroscience needs to be sensitive to considerations of computing.
1. Some cognitive tasks are carried out more quickly than can be accounted for.
You can work out how long this would take the brain if it were a serial computer and the neurones were wires. It is much longer than the time actually taken.
Visual recognition is an example.
2. Anatomically and physiologically, the brain seems not to be a serial computer. Each neurone is connected to many others in a complex ramifying network. This isn't how the components of a serial computer are connected up.
3. Data Storage:
Information seems not to be stored in the brain in the way that it is stored in a serial computer. There don't seem to be blocks of neurons where data is stored. Instead, data seems to be stored in the connections between the same neurones that are carrying out the processing. Memories seem to degrade when the system is damaged, rather than get wiped out one by one.
4. Some tasks we find easy are proving very difficult to simulate on a serial computer. Recognizing faces is one example. Also, some things we find quite difficult are easy to program on a serial computer - e.g. simple proofs in maths or logic.
5. The hardware/software distinction is not easy to apply to the brain.
6. There are probably many more levels of organization in a brain than in a serial computer.
7. Processing in non-verbal animals and preverbal human beings is surely likely not to involve language-like operations.
Work on connectionist nets is valuable not only because it gives us an alternative to the idea that all representation in the brain must be 'language-like' and all computation 'logic-like.'
"They thus free us from what Hofstadter called the Boolean Dream, where all cognition is symbol-manipulation accordng to the rules of logic." C&S p. 149.
END
Revised 26:03:03