Connectionism

So far we have been taking it that the brain as computer option involves the brain in manipulating representations according to rules.

This comes out in

• Chomsky's account of language interpretation and processing
• Fodor's argument that there must be a structured language of thought.
• This representationalist model pictures the brain as a von Neumann computer.

A Reminder: The von Neumann Computer

What is a von Neumann computer? It is a computer which has a single main processor, with access to memory. All it does is carry out operations of the following sort.

Take whatever is in memory location M1.

 

Early stored program machine at the Institute of Advanced Study at Princeton, inspired by John von Neumann, completed 1952. From V.Pratt, Thinking Machines, Oxford, 1987, Blackwell, p.168

Perform operation O upon it.

Put the result in location M2.

Any given computation is made up of sequences of such operations, often very long.

The thing which determines which operations are carried out and which order is the program. A program is a long list of operations.

An example of an operation would be: 'add 1 to it', another: 'add it to whatever is in memory location M3'.

So a particular instruction might be:

Take whatever is in memory location 343567

Add 1 to it

Put the result in location 343567.

The repertoire of elementary operations of which a given computer is capable is small and as simple as the examples given:

John von Neumann 1903-57. From V.Pratt, Thinking Machines, Oxford, 1987, Blackwell, p.166.

Add

subtract

check if it's the same

check if it's bigger than

All the many things that computers can do are built out of sequencing these simple operations.

We can start.

Keep doing this

Take whatever is in memory location 343567

Add 1 to it

Put the result in location 343567.

There are a number of reasons to think this model of brain functioning may be wrong. We will turn to those in a moment.

But first let me sketch an alternative: the connectionist model.

Connectionist systems

Diagram of connectionist net: thanks to Churchland & Sejnowski, in the Reader, 2nd edition, p.142

Here is a simple connectionist system:

The connectionist computer consists not of one central processing unit (CPU) with access to memory but of a network of 'nodes'. Each node is capable of being in a state of activation.

Let us think of the simplest set-up.

There are just two states of activation for each node - on or off.

Sometimes it is activated and sometimes not.

Connections run out from each node to several others. When the node is activated its connections go live.

What switches a node on? The state of its connections.

One simple rule would be: Only switch on when all your connections are live.

Another would be: Switch on if and only if two of your connections are live (So if three are live, you are off).

A given system will be set up according to a regimes of this sort - there will be a rule governing when a node is on and when a node is off.

Think of the nodes as set up in a rectangle

If you think of the nodes as arranged in a rectangle, the network is experimented with as follows:

The line of nodes on the bottom edge of the rectangle are subjected to a pattern of activation. These we can call the input layer.

This causes certain nodes throughout the system to become active.

The input stimulation will initiate activation in some of the nodes to which the input nodes are connected.

A wave of stimulations will pass into the network.

As a node becomes active its connections become live. Depending on what other stimulations it is getting, a node thus in receipt of stimulation will possibly be activated. If so it will pass on a stimulus to all the nodes it is connected to.

But one of the nodes it is connected to will be the node that helped stimulate it.

So you might expect, once you have input a pattern of stimulation onto the input layer, nodes in the rest of the rectangle will switch on and off and on and off - will twinkle in fact, as stimulations flow this and that throughout the network.

Sometimes at least what is found experimentally is that after a time the pattern of activity across the network settles down and you get a steady state. If you consider the top edge layer of the rectangular network, that layer sometimes comes to show a steady pattern of activity. This layer is called the output layer.

The pattern of activity put into the input layer is called the problem. The pattern of activity that gets established at the output layer is called the solution.

It is understood that no one knows quite what goes on the in the middle. There is just a complex of interconnected nodes, which switch on and off though according to a particular regime.

That's it really.

We ought to try it.

Please do as follows:

Everyone on the front row sit tight.

Everyone on row two look to the front and write down the names of two people to your front. What matters is that you fix on two people and forget everybody else. Tell them.

Then look round and fix on two people behind you. Write their names down. Tell them.

Everybody on Row 2 now knows what they are connected to.

People on row three.

Write down the names of those in the row in front who tell you they have fixed on you.

Then turn round and fix on two people in the row behind you. Write down. Tell.

Everybody on Row 3 now knows what they are connected to.

Row four

As for row three.

Final row

Same as row in front except you won't need to turn round. You will just be connected to the people in front.

You are the output row.

You are now connected into a network.

A node is live when it has its hand raised.

______________________________

Rules to try:

Go live if any of your connections is live.

I will set up the input.

(Make every alternate input node live)

When I have done so, follow the following rule:

Review all your connections (four for most of you.)

PASS ONE.

Put your hand up if any of your connections are live.

PASS TWO

Now check again and adjust your hand accordingly.(Pass two.)

PASS THREE.

Now carry on keeping adjusting your hand depending on a constant review of your inputs.

Do we get a stability?

Explore different rules.

Rule 2

Put your hand up if one or two but no more than two connections are live.

(So if three connections are live, you go off.)

Stick with Rule 2.

Who would like to try an input which produces no steady state?

NETtalk

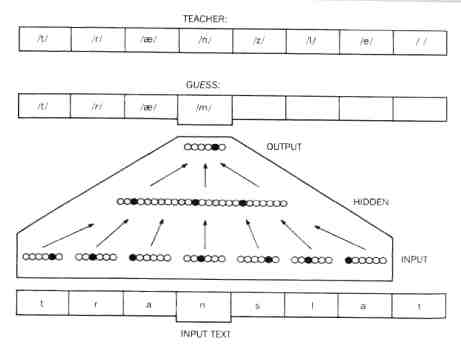
A complication was introduced into one of the most interesting set-ups of this kind. Connections were made to be of varying strengths. So whether a node went active or not would depend on what connections were active, but also on how strong those connections were.

This is the set-up known as NETtalk.

Written words were coded in at the input end.

The 'solution' was compared with a set of arbitrary codes for sounds.

When a steady state was achieved with a certain input, a sound would be emitted, depending on what the output was.

At first of course there was no relation between input word and output sound. All the sounds would be 'wrong'. If you input the first syllable of Shed' the output might be 'p'.

But each time the output sound was not right, the weightings of the connections between the nodes in the middle of the net were altered.

And if this produced a closer result, they were altered in the same direction some more: until the right sound was produced.

The system gradually learnt to speak.

Is that amazing?

Difficulties with representational theory of thought.

1. Some cognitive tasks are carried out more quickly than can be accounted for.

You can work out how long this would take the brain if it were a serial computer and the neurones were wires. It is much longer than the time actually taken.

Visual recognition is an example.

2. Anatomically and physiologically, the brain seems not to be a serial computer. Each neurone is connected to many others in a complex ramifying network. This isn't how the components of a serial computer are connected up.

3. Data Storage:

Information seems not to be stored in the brain in the way that it is stored in a serial computer. There don't seem to be blocks of neurons where data is stored. Instead, data seems to be stored in the connections between the same neurones that are carrying out the processing. Memories seem to degrade when the system is damaged, rather than get wiped out one by one.

4. Some tasks we find easy are proving very difficult to simulate on a serial computer. Recognizing faces is one example. Also, some things we find quite difficult are easy to program on a serial computer - e.g. simple proofs in maths or logic.

5. The hardware/software distinction is not easy to apply to the brain.

6. There are probably many more levels of organization in a brain than in a serial computer.

7. Processing in non-verbal animals and preverbal human beings is surely likely not to involve language-like operations.

END