Reduction of general graphs using minimum number of edges

Graphs with highly connected nodes are widely used in various application, the complexity of which makes it difficult to read and digest. Edge compression offers a tool to re-organize the structure of the graph through clustering the nodes which shares the similar neighbors in one supernode, by doing so, we could reduce the number of edges while without losing any details (connections). In order to maximize the profit brought by the edge compression technique, we seek for the reduction of a general graph to have minimum number of edges.

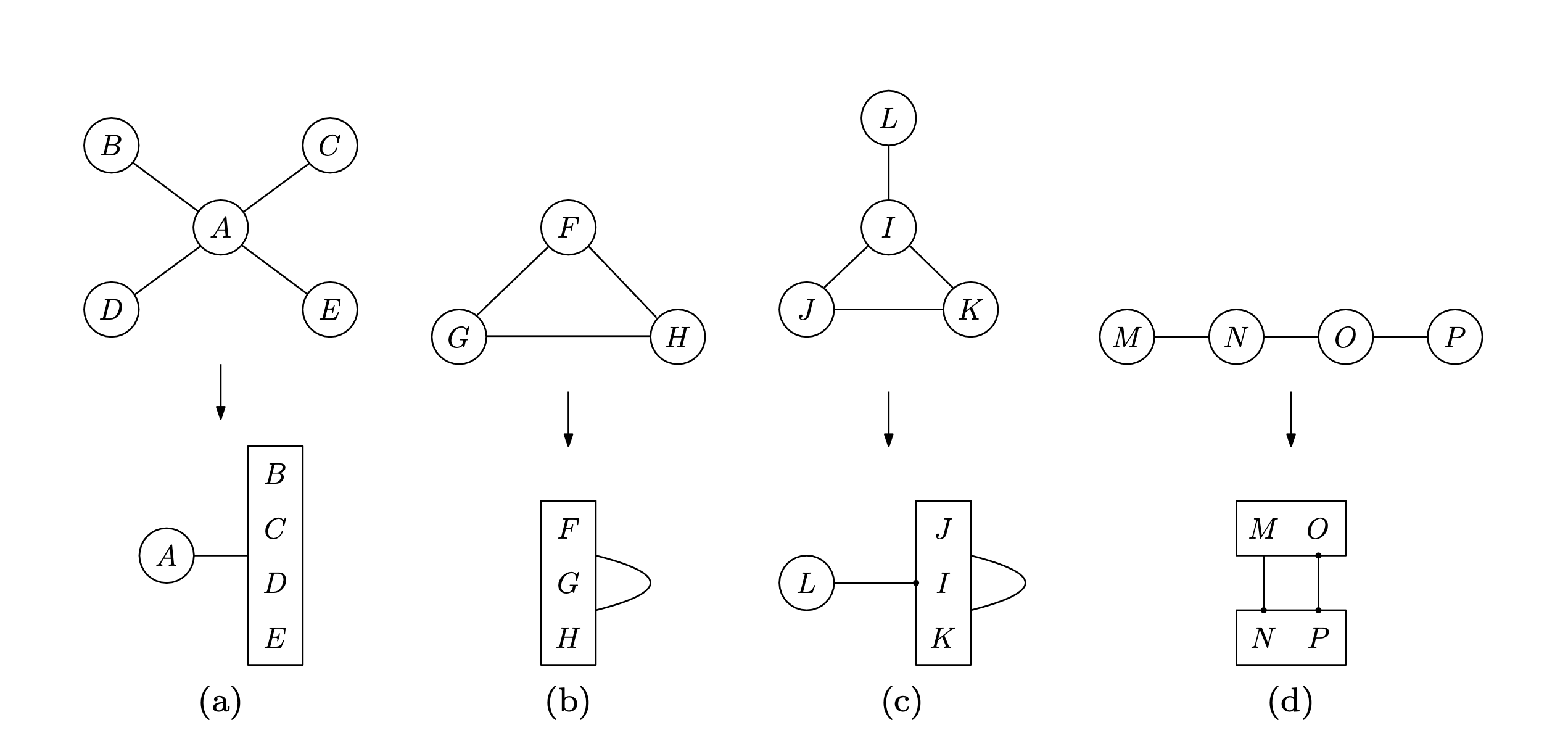
Using the method of edge compression, nodes that are topologically equivalent can be clustered in one block. It is immediate that the edge between one node and one supernode indicates the connection between the node and each equivalent node in the supernode. A supernode is an aggregated set containing at least two nodes that share similar neighbours. See Fig 1 (a) as an example of supernode.

Moreover, the definition of block allows edges to cross block boundaries and connect with specific node as shown in Fig 1 (c). For simple undirected and unweighted graphs, the edge compression method is lossless with the compressed graph carrying exactly the same ‘connection’ information as the original graph. The actual way of edge compression depends on different structure of graphs, while we propose optimal solution of edge reduction for regular and less complex graphs, benefiting our algorithms for many other graphs.