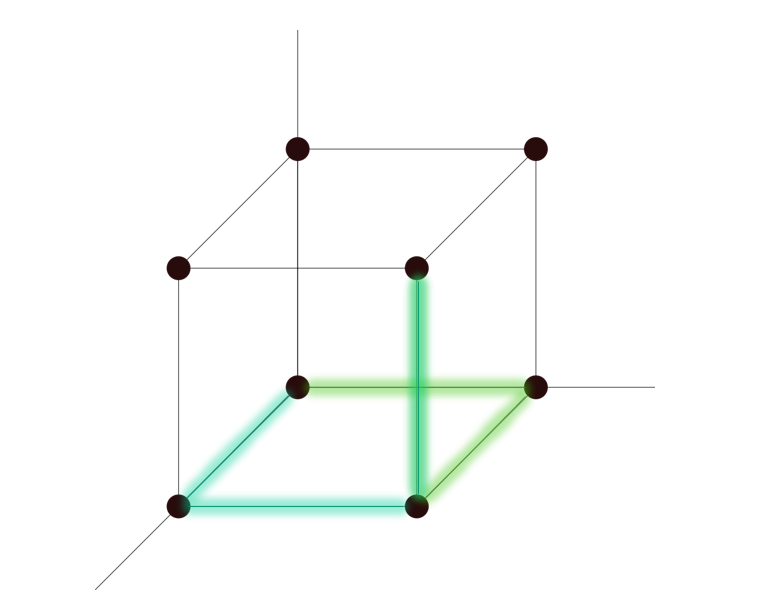
My Master’s Project is on Accessibility Percolation, a term coined by Nowak and Krug [1]. In short, consider a graph on which each edge is assigned a uniform U[0,1] random variable, a path on this graph is said to be accessible if the numbers along the path are increasing. We look at the probability of such types of paths existing under certain conditions on specific types of graphs.
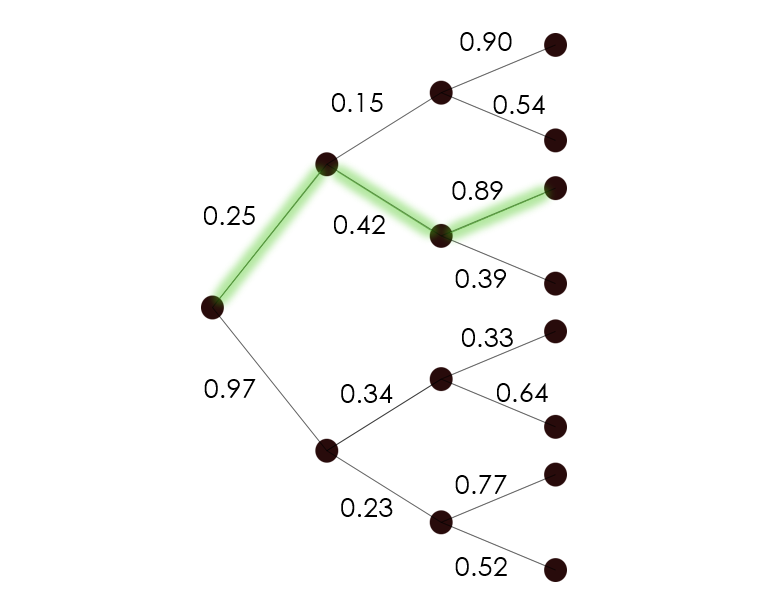
The project follows the proofs of the theorems found in Roberts and Zhao [2] and Berestycki, Brunet and Shi [3], which study increasing paths in regular trees and increasing paths in the irregular trees and the hypercube respectively. Please find a link to the project below:
[1] Stefan Nowak and Joachim Krug. “Accessibility percolation on n-trees”. In: EPL (Europhysics Letters) 101.6 (2013), p. 66004.
[2] Matthew Roberts and Lee Zhao. “Increasing paths in regular trees”. In: Electronic Communications in Probability 18 (2013), pp. 1–10.
[3] Julien Berestycki, Eric Brunet, and Zhan Shi. “The number of accessible paths in the hypercube”. In: Bernoulli 22.2 (2016), pp. 653–680.