I have recently learnt how to solve some mathematical programming problems using Gurobi, an optimisation solver, in Python. Before joining the STOR-i programme, I was a complete novice at programming in Python so getting to grips with it is really exciting! One of the problems Gurobi is especially useful for is a standard linear programme. In this blog post, I’m going to introduce how we can use Gurobi in Python to solve linear programming problems.
A trope of a linear programming class is the furniture factory example. No doubt, if you’ve learnt anything before about linear programming you would’ve heard of it. It concerns a factory that makes chairs and tables, with specification on the materials and working hours needed to complete production as well as the profit generated from the production of a table and a chair. The question proposed is, with given constraints on material and working hours, how many chairs and how many tables should be made in order to maximise profit? Not that I’m bored of seeing this problem (I really, really am) but I thought I could illustrate how we can use Gurobi using an alternative example, one inspired by my family’s love of music and my Dad’s very real problem of buying the right boxes to store his extensive record collection.

I was brought up surrounded by music, in a house with multiple jukeboxes so my family has a lot of vinyl! They’re our pride and joy and so we want to store them safely in a way that allows us to access them easily (because let’s be honest you never know when you’ll just need to find Spice by the Spice Girls). We have done extensive research across the storage market (makes for thrilling weekend activity I must say) and we have two box contenders. The differences in the boxes are displayed in the table below:

We need to make sure that all seven-hundred of our records are boxed and my Dad wants to buy at least eight boxes so that we have enough space for the records he keeps treating himself to in order to stay sane during the lockdown. As you may have realised, storage is big business, these boxes are expensive, so we want to minimse our cost as much as we can.
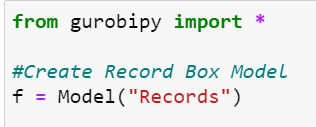
Let’s solve this problem and figure out how many of each box to buy. Before you use Gurobi, you’ll have to install it and get a license, more information on that can be found here. When you’ve got Gurobi working fine and dandy on your computer the first thing we want to do is set up our model. Here we’ve called our model f and added a label “Records”.
We then create our variables. These are the two different boxes we can buy. As we can’t buy a fraction of a box, we specify that our variables are integers by using vtype=GRB.INTEGER. Other variable types are listed in the Gurobi documentation here.

Our objective function is to minimise the cost of buying the boxes. We set the objective of our model f by using .setObjective and include GRB.MINIMIZE to specify that our problem is a minimisation problem. For a maximisation problem, we would alternatively write GRB.MAXIMIZE. Don’t forget to spell the American way!

The constraints of our linear programming problem involve the requirement for all of our records to be placed in a box and that we order at least 8 boxes to ensure there’s room for purchases in the near future. We use .addConstr to add these considerations to our model f.

To solve the problem we use the .optimize() command. To print the variable outcomes we use .getvars().

If we run all of this code in Python we get our solution!

In order to minimise cost, we should buy two of the smaller box, Box 1, and six of the larger box, Box 2. The total cost will be £130. It’s as easy as that!
So what do you reckon? Is Gurobi a sound tool? I think so. This problem might be a simple example but it illustrates how we can use Gurobi to model and solve mathematical programming problems effectively. Be sure to check out the Gurobi tutorials in the Want to Know More section below.
Before I go, I thought I’d share my family’s vinyl collection must-haves just in case you fancy starting your own. But, fair warning, before long you might end up having to spend £130 on some storage boxes!
- Dan Fogelber – Phoenix
- David Bowie – Station to Station
- HAIM – Something to Tell You
- Buddy Holly – Buddy Holly
- The Rolling Stones – Sticky Fingers
- The Animals – The Animals






This week’s tweet of the week goes to @averageacademics with an excellent reminder to step away from the screen once in a while.
Missed my last post? Check it out here.
Want to know more?
Gurobi offer a selection of tutorials to get to grips with the software for linear programming problems. You can find it all at the link below:
