I recently learnt about Markov Decision Processes (MDPs). These are sequential decision processes, commonly found in the real world where decisions need to be made in an environment with uncertainty. Solving these problems, especially when they are large, is a big challenge. During my research of MDPs, I learnt these processes are pretty much everywhere, present in industries like finance, manufacturing and aviation to name just a few. Although, what I was most excited to discover was that playing a game of Tetris, believe it not, embodies this mathematical framework. As a 90’s baby, becoming freakishly addicted to Tetris felt like a rite of passage. I can remember stealing my sister’s Gameboy and desperately trying to erase her high score before she noticed. I couldn’t wait to write this post but before we dive straight in to the fun of addictive block building, let’s start with the basics.
In decision processes we can have multiple actions that produce different outcomes that have different likelihoods of being selected and resulting benefit. In these processes, a decision maker wants to make the best choices and so a solution is formed by the development of a policy which informs the decision makers on which decisions to make. An MDP is made up of states, actions, transition probabilities and rewards. A transition probability is the probability of changing from one state to another for a given action. The reward is the reinforcement given for taking a specified action. MDPs satisfy the Markovian property, so that the chance of moving from the current state depends only on the current state and not previous states or actions.
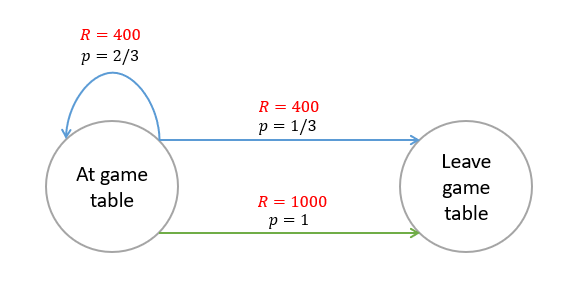
Imagine you’re in post-COVID-19 world, in a casino and sitting at a game table. In each round if you choose to play the game you will get a reward of £400 and, with probability two-thirds, the chance to play again. However, with probability one-third the game ends and you have to leave the table. You can also choose not to play and in this case you’ll get a reward of £1000 but you have to leave the table. This example forms the MDP visualised above. The states are ‘at game table‘ and ‘leave game table‘. The blue arrows represent the action ‘play‘ and the green arrow represents the action ‘don’t play‘. The rewards are either £400 or £1000 depending on the action chosen. The probability of transitioning from state ‘at game table‘ to ‘leave game table‘ is 2/3 and 1 for action ‘play‘ and ‘don’t play‘ respectively.
In Tetris, the states are represented by the configurations of the wall and the current falling piece. Actions are formed by the possible orientation and placing options of the current falling piece. The reward is the number of deleted rows and associated points awarded after the placing of the current falling piece. The terminal state of Tetris is the configuration of the wall at maximum height prompting the game to end. The objective is to maximise the number of deleted rows that generate points. Solving this MDP would aim at generating a policy that maximises the expected number of points won during play. So, is everything falling into place? (Sorry, I couldn’t resist.)

How do we solve an MDP? Well, for simple examples like the casino game we’d look to Dynamic Programming. This class of algorithms work by breaking down the problem into sub-problems and are effective for relatively small problems. However, for MDPs with a large number of states, like playing a game of Tetris, these methods aren’t enough.
That’s where Approximate Dynamic Programming comes in. These approaches work by taking on a small part of the process and generalising this for the entire decision process. One of these methods is called Value Function Approximation. The aim is to create a function that approximates the value, a measure of how good it is to be in a state, for every state in our MDP. In Value Function Approximation with Linear Methods we approximate the value function by writing it as a linear function of features. These features give us information about the states. In our Tetris example, they tell us about configurations of the wall.
We can then estimate the value of the current state, the current configuration of the wall, by applying the knowledge of how good it is to have the configurations given by the features. We estimate the current state, the current configuration of the wall, by taking a weighted sum of the information provided by the features.
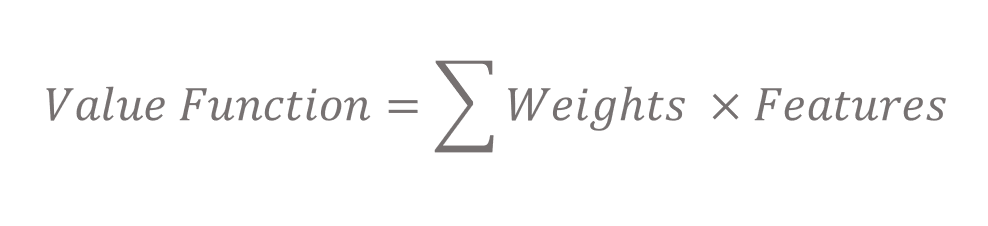
We can use a Stochastic Gradient Descent method which minimises the expected mean square error between the approximate value function and the true value function. With each iteration we update the weights using a simple update rule. We specify a step size and we define an error as the difference between the true value function and our current approximation.
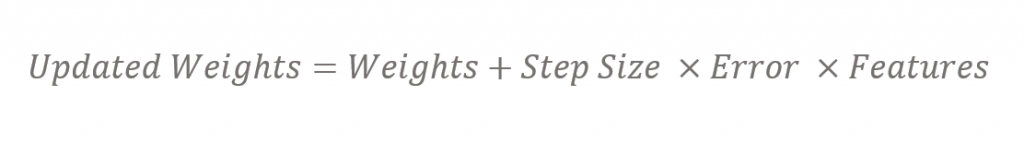
This method will converge to a global optimum and therefore we will successfully get an approximation to the value function. Then we know how good a policy is! How great! Though, in real life things might not be this simple as this as we don’t know the real value function that gives us the error (if we did I’d already be killing it at Tetris). In place of the true value, we use the return, the reward generated, following each state which is an unbiased approximator of the true value. Our error is then given by the difference between this return and our current value approximation. This process is known as Monte Carlo Linear Value Function Approximation.
Many industries have a need to optimise decision making and these problem have the form of a Markov Decision Process. In most of these real world scenarios the problems are so big we need to use approximation methods. This is what makes methods like Value Function Approximation so significant. And who knows, if I had it up my sleeve back in the 90’s maybe I could’ve crushed my sister’s high score!
That’s it for now, just got time for my tweet of the week! This week’s goes to @averageacademics! Check back soon for more blog posts!
Missed my last post? Check it out here.
Want to know more?
David Silver’s lecture on Value Function Approximation can be found here.
M. Hadjiyiannis, 2009. Approximate dynamic programming: Playing Tetris and routing under uncertainty.


