Due to lockdown restrictions, that prevent me from coming back to Lancaster, I am currently working from home back in my hometown. Alike many of us, this leaves me short of like-minded people to excitedly discuss my ideas with. So, once I read a really interesting paper about the industrial use of helicopters to transport workers to offshore installations, I shared my enthusiasm with my Dad (who has perfected the art of nodding along). The paper specifically looks at minimising the number of passengers exposed to the most risky phases of travel, takeoffs and landings, using a particular part of Operational Research that I am really interested in, Scheduling. Whilst telling my Dad about what I’d learnt, I was surprised to find out that he had worked on offshore installations as a Field Service Engineer. He told me about his experiences and I was hit with the shocking realisation that, before having me and my sister, my parents actually had their own lives! If you look closely on the photo below you can see the words “Gulf Helicopter” written on the side of the chopper. The images in this post are my Dad’s (thanks, Dad!) and were taken whilst he was working in the Gulf in the early 1980s.

So, how can scheduling minimise the risk for offshore workers like my Dad? First, consider that the takeoff and landing risk is a product of the probability of an accident occurring during takeoff/landing, the total number of people exposed to takeoffs/landings and the probability of a fatal outcome as a result of an accident occurring during takeoff/landing. The former and the latter are assumed probabilities, 0.65 in a million and 1 respectively. Therefore, the takeoff/landing risk is minimised by minimising the number of people exposed to takeoffs/landings. Given a number of installations with varying pickup demand, referring to the number of workers needing to be picked up from an installation, the aim is to find a feasible schedule that collects all the workers and minimises the total number of people exposed to takeoffs and landings.
Let’s consider just a single flight path. So we have one helicopter that has to pick up workers from all installations and we assume that the total pickup demand does not exceed the capacity of the helicopter.

This problem and its solution are identical to the scheduling problem of processing a number of jobs on a single machine with the aim of minimising the total completion time. The solution, proved by Smith in 1956, involves scheduling jobs in the non-decreasing order of their processing times. In the instance of transportation to offshore installations, installations represent the jobs needing to be processed and the number of offshore workers in need of pickup mirror the processing time of these jobs.
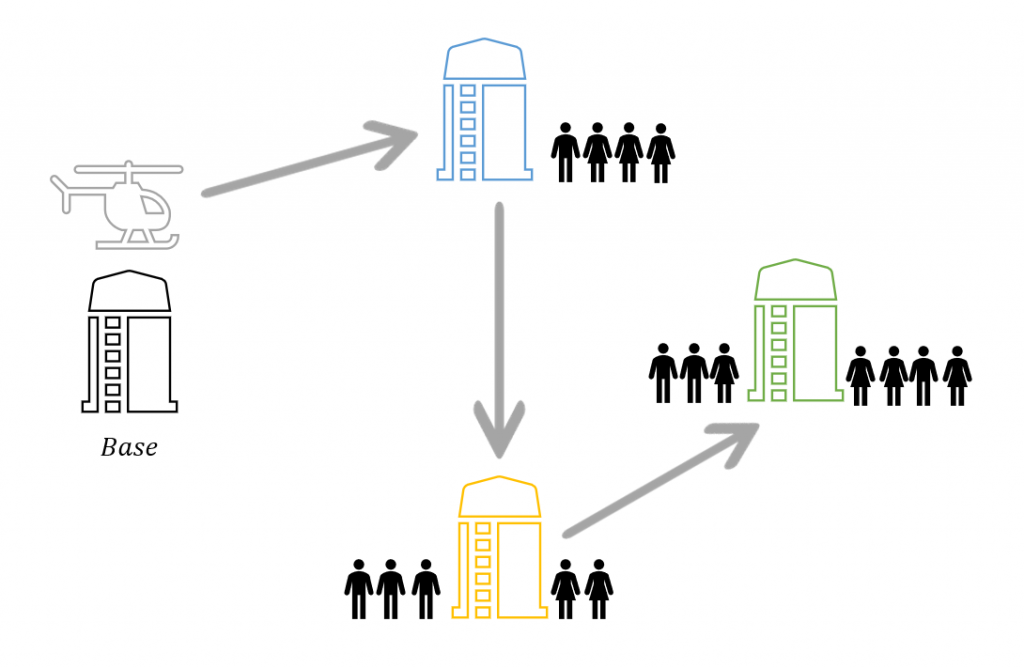
So the permutation of installations that minimises the risk can be found by a visiting the installations in order of the number of workers that need to be picked up, from smallest to largest. In the example above, the helicopter starts at the base heliport and should visit the installations in the order, blue, yellow, green and then return to the base. This feels fairly intuitive. We visit the installations with the most people last, as to avoid exposing more people to unnecessary risk of further takeoff and landings. The risk, the total number of people exposed to takeoff/landing risk, is given by adding together the number of workers at the green installation, twice the number of workers at the yellow installation and three times the number of workers at the blue installation. This is because the workers at the blue installation are exposed to a takeoff/landing three times, the workers at the yellow installation two times and those at the green installation just once. The total risk is equal to 29. The risk in terms of the expected number of fatalities can be obtained by multiplying this value by the assumed probability of an accident and the probability of fatality as a result of an accident as defined above.
Imagine now we have more than one helicopter, and thus more than one flight path. How do we decided which helicopter visits which installation and in which order? This problem is identical to a scheduling problem on parallel machines which seeks to minimise the completion time. The machines in this context are represented by the helicopters. The algorithm that solves this problem was proved by Conway, Maxwell and Miller in 1967. The schedule is found by following these steps:
- Forming a list of in the installations in non-decreasing order of the number offshore workers needing to be picked up.
- Considering installations in this order assign the next installation to the helicopter that has the smallest number of offshore workers currently assigned until there are no installations left.
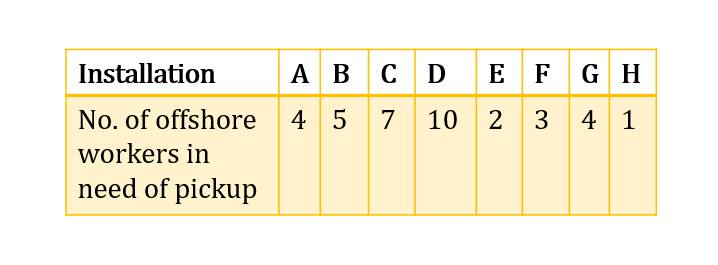
Take the following example. We have eight installations that need visiting, labelled from A-H, and three helicopters, orange, purple and red.
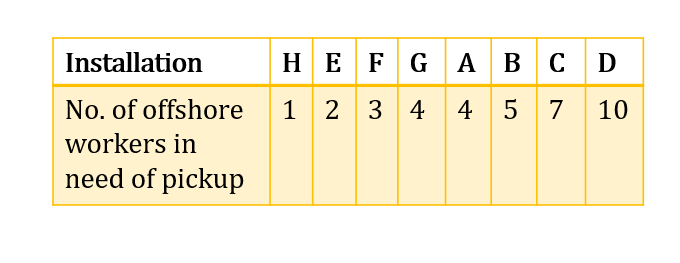
We organize the list of installations into non-decreasing order.
We schedule flights to installations in the order H, E, F, G, A, B, C, D assigning the next installation to the flight with the least load.
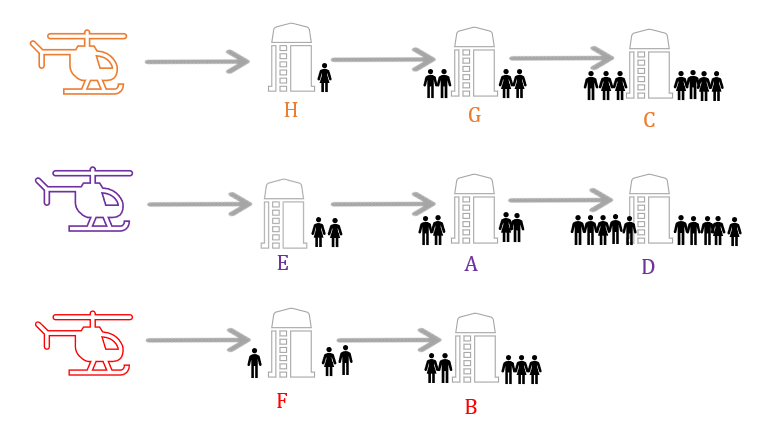
The risk for the flight path of the orange and purple is given by adding together the number of workers at the third installation, twice the number of workers at the second installation and three times the number of workers at the first installation in each of their schedules. The risk for the flight path for the red helicopter is found by adding the number of offshore workers at installation B and twice the number of workers at installation F. The total risk is given by adding up the risk of all flight paths and is therefore equal to 53.

So, minimising passenger risk during takeoff/landing in this context provides problems with are identical to known scheduling problems! This is great because we already have algorithms to solve so many of these problems. The link between a safe transportation problem and scheduling offers an alternative way for industry to organize the pickup of their workers. This perhaps contrasts to proposed routes found by vehicle routing techniques, for example, with the advantage of prioritising worker safety. The paper that inspired this post considers so many more variations to the pickup problem. I’ll leave details below so be sure to dive in!
Check back soon for more posts! Missed my last one? You can view it here.
My tweet of the week goes to @alrightPET, who, I think, raises a very valid point.
Want to know more?
Conway, M. and Maxwell, W., 1967. Miller, Theory of Scheduling. Reading: Addison Wesley.
Smith, W.E., 1956. Various optimizers for single-stage production. Naval Research Logistics Quarterly, 3(1-2), pp.59-66.
Here’s the paper this blog post is based on:
Qian, F., Strusevich, V., Gribkovskaia, I. and Halskau, Ø., 2015. Minimization of passenger takeoff and landing risk in offshore helicopter transportation: Models, approaches and analysis. Omega, 51, pp.93-106.
I found the following book really helpful when learning about scheduling models and algorithms:
Pinedo, M., 2012. Scheduling (Vol. 29). New York: Springer.