Hello and welcome! This blog post is my second in a new series of regular posts as part of my journey as an MRes student at the STOR-i Centre for Doctoral Training. Strap in, because boy have I got a big scoop for you!
We know mathematics has successfully elucidated many phenomena, from space travel to climate change, but what about one of the most famously posed questions in the history of literature? Can mathematics really turn its hand to the arts? Cue Shakespeare and his most famous play, Hamlet. Historically, the character Hamlet is regarded as a crazy, irrational protagonist but is he truly mad?

Source
Well, in his book Game Theory and the Humanities: Bridging Two Worlds, Steven J. Brams argues not. Using the Theory of Moves he presents an explanation for Hamlet’s famously erratic behaviour. The theory aims to bring a dynamic element to standard Game Theory and strives to better emulate the realistic expectation of humans in strategic situations. As a result, the Theory of Moves postulates that players think ahead to the consequences of countermoves.
The Theory of Moves is bound by certain rules. The first defines an initial state, found at the intersection of a row and column of a payoff matrix, where play begins. Secondly, any player can unilaterally switch their strategy, thereby changing the state of the game from the initial state. In response, the other player can also change the state of the game, by unilaterally switching their strategy. From here, the first player can then choose again to change their strategy and thus the state of the game. This alternation continues until the game ends in a final state, which is the outcome of the game. The final state occurs when the player whose turn it is to switch strategy, chooses not to do so. Further conditions clarify that a player will not choose to change their strategy unless the change moves the game to a state that is preferred by that player and this change is not the initial state. That all may sound pretty confusing so let’s see an example!
Consider the central conflict in Shakespeare’s play between Hamlet and his father’s (the King’s) murderer, Claudius. If we model this conflict in a game-theoretic way we can summarise Hamlet’s strategies as either to expose Claudius as the King’s killer or to remain quiet. Claudius’ strategies are to kill Hamlet or let him live. We then have four possible outcomes which can be ranked from each characters perspective from best to worst.

Following the rules set out above, the Theory of Moves works by moving around the table above as follows. This particular conflict starts in the state at the bottom right of our table. Hamlet is currently hiding the knowledge about his father’s murder and Claudius has not yet decided whether Hamlet poses a significant enough threat to kill him.
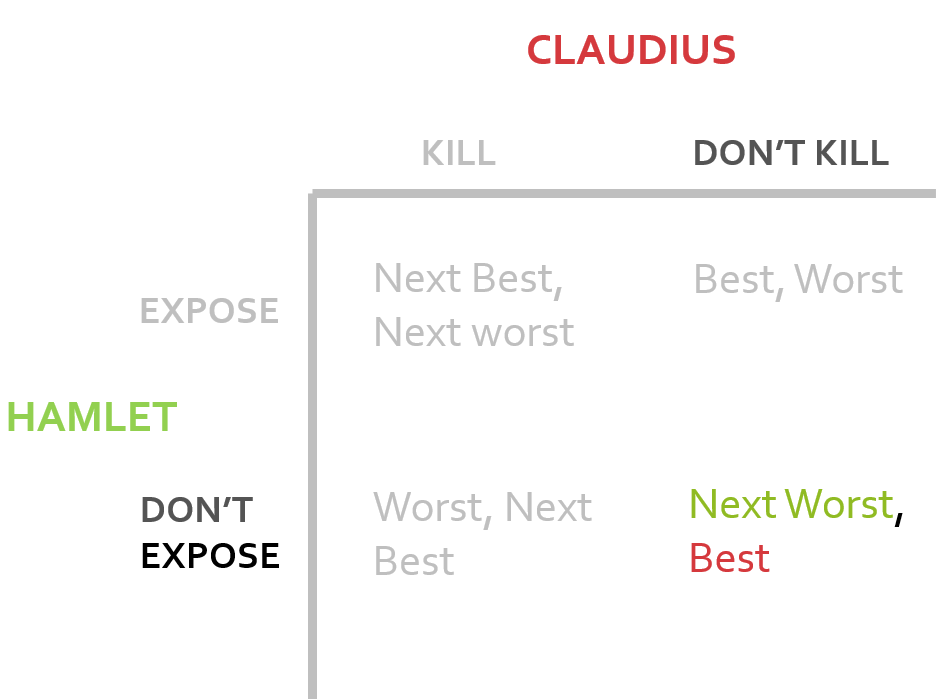
A better outcome for Hamlet occurs if he switches his strategy and reveals Claudius as his father’s murderer. Therefore, we move up the table to the top right.

This is then the worst result for Claudius so he should opt to change his strategy from don’t kill to kill. Now, we’re in the top left state where neither Claudius or Hamlet can benefit from changing their tactic. This state is know as the nonmyopic equilibrium, the state at which neither player, considering all possible countermoves, has an incentive to move from. Therefore, this is the end of the game.

Let’s compare this analysis with what really happens according to Shakespeare. In the play, Hamlet gains information that confirms Claudius as the King’s killer and plots to kill him but Claudius realises that Hamlet knows the truth and in turn sets a plan to silence Hamlet. In the end, Hamlet exposes Claudius as his father’s murderer but succumbs to a wound from a weapon poisoned by Claudius. The story follows the exact path we set out above which is defined by the Theory of Moves. This suggests a presence of rational actions providing an argument for Hamlet’s levelheadedness, a view that contradicts classic interpretations of the play. So we not only have literary analysis but also a plot thread determined by a mathematical technique. Woah!
Hamlet isn’t the only work to fall into the grasp of game theoretic analysis. Many distinguished works are among those studied through a game theoretic lens, including detective stories by Edgar Allan Poe, Wagner’s Tannhäuser and Puccini’s well-renowned opera, Tosca. Let’s head into the 21st century and look at the cultural phenomenon Game of Thrones. It’s the HBO TV adaption of a series of books by George R. R Martin and at its height had a soaring episode budget of fifteen million US dollars, earning it the title of the most anticipated show of 2019. Unfortunately, the final season was bathed in controversy as the show disappointed fans across the globe with its final character arcs and plot.
It wasn’t just Twitter that was angry. A petition titled ‘Remake Game of Thrones Season 8 with competent writers’ has (at time of writing this post) 1,843,362 signatures. So, could maths help explain what went wrong?
Well, how about we take it all the way back to the end of the seventh and penultimate season. In the seventh episode, The Dragon and the Wolf, sparring characters Daenerys Targaryen and Cersei Lannister both face a strategic decision, to call a truce, in order to exchange information and take a step towards an alliance or remain adversaries and refuse to meet. Essentially they both have two strategies, to meet or to reject the truce. We then have four outcomes:
- A truce is secured, Daenerys can present her information to Cersei and they can take a step towards an alliance.
- Cersei severs any possible relationship avoiding the risk of attack. She leaves Daenerys at risk from attack in King’s Landing.
- Daenerys avoids the risk of attack but leaves Cersei insulted and without information. The rivalry between the pair is worsened.
- No truce is secured. The external threat remains.
Let’s analyse using the Theory of Moves.
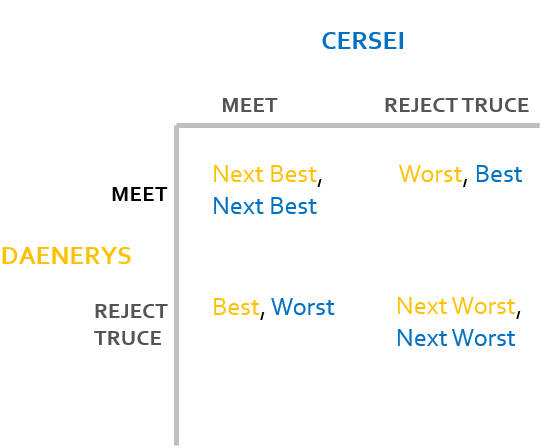
The game begins in the 2nd state, the top right in our table.
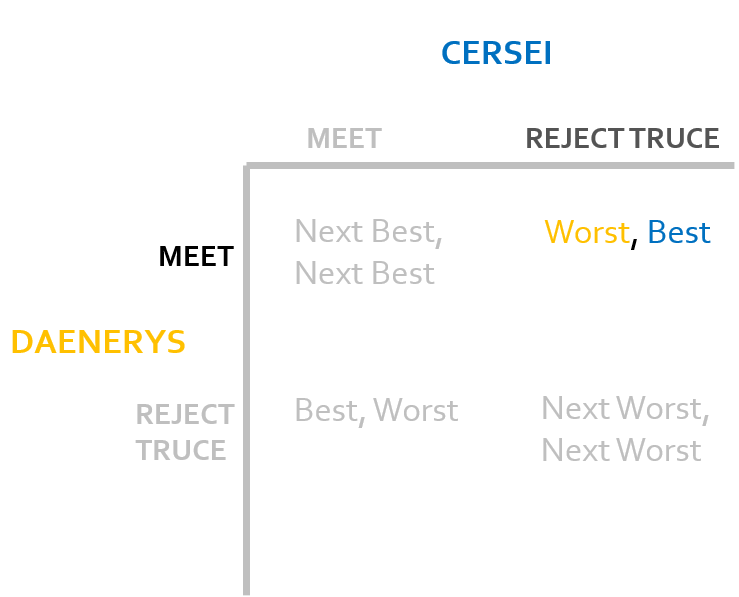
From here, Daenerys should change the state of the game to the 4th outcome by switching her strategy and ensuring herself a better conclusion. Therefore we move to the bottom right of the table.
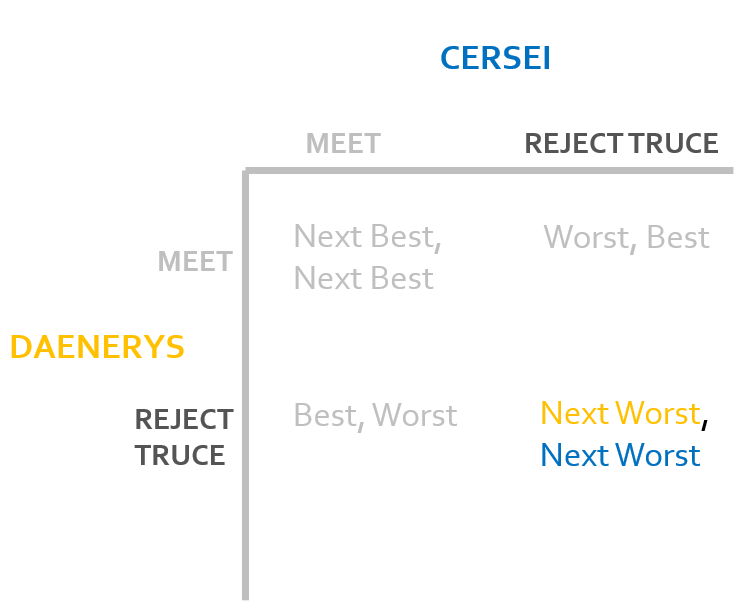
Cersei has no reason to change the state of the game from here, as a change in her strategy would result in the state of the game that gives her her worst outcome. Therefore, the game ends and this state is the nonmyopic equilibrium of the game.
Interestingly, the nonmyopic equilibrium does not align with the outcome reflected in the narrative of the story. Instead, the episode grants the viewers the first ever meeting of these characters, as both engage in a truce, synonymous with the first outcome, the top left in our table. With the Telegraph describing this meeting as a ‘hokey twist’, this episode marked the beginning of the controversy that surrounds the later seasons of the show. So, could this be where it all went wrong?
Anyone that has watched Game of Thrones knows it has a vast, complex plot which could be entirely explored using game-theoretic methods. Analysis of this kind could perhaps allow for us to verify storylines and predict engaging and satisfactory narratives. Although perhaps unlikely bed fellows, from Shakespeare to binge-worthy boxsets, storytelling and mathematics seem to come together here to provide interesting insights.
That’s all for now! This week’s tweet of the week goes to @SarlCagan93. I feel you, David.
Check back soon for more posts! (If you missed my last one, you can check it out here.) In the meantime, if anyone knows how to go about explaining working hours to a dog please get in touch!

Want to know more?
Brams, S. (1994). Theory of Moves. 1st ed. Cambridge: Cambridge University Press.
Brams, S. (2011). Game Theory and the Humanities: Bridging Two Worlds. Cambridge, Massachusetts. London, England: The MIT Press.
Chrissochoidis, I. and Huck, S. (2010). Elsa’s reason: On beliefs and motives in Wagner’s Lohengrin. Cambridge Opera Journal, 22(01), pp.65-91.
Chwe, M. (2013). Jane Austen, Game Theorist. Princeton and Oxford: Princeton Univ. Press.
Deloche, R. and Oguer, F. (2006). Game Theory and Poe’s Detective Stories and Life. Eastern Economic Journal, 32(1), pp.97-110.
Power, E. (2017). Game of Thrones season 7 episode 7 review: The Dragon and the Wolf gave us betrayal, nudity, and game-changing twists. [online] The Telegraph. Available at: https://www.telegraph.co.uk/tv/0/game-of-thrones-season-7-last-episode-review-dragon-wolf/.