Related Phenomena
In my past few posts I’ve attempted to give a bit of an informal introduction to the main ideas behind extreme value theory: from motivating it the field with unfortunately close to home examples, to discussing different approaches we can take. One thing all the theory I’ve covered so far is that it only considers the extremes of one variable, i.e. the univariate case. When you think to many settings where you might want to apply these methods, you could also begin to ask another question; what about when two or more variables are related somehow? Does this increase the chance of them being extreme together? And if so, how does this affect our design and risk assessment examples? These questions motivate the extension of extremes methods to the multivariate setting.
An Oceanic Example
A big motivator for this kind of thinking is in the design of ocean structures such as oil rigs, sea walls, and ships. Certain combinations of variables such as wave height and windspeed can provide critical conditions that result in failure of these structures. The design process thus needs to take into account the most likely combinations of these variables.
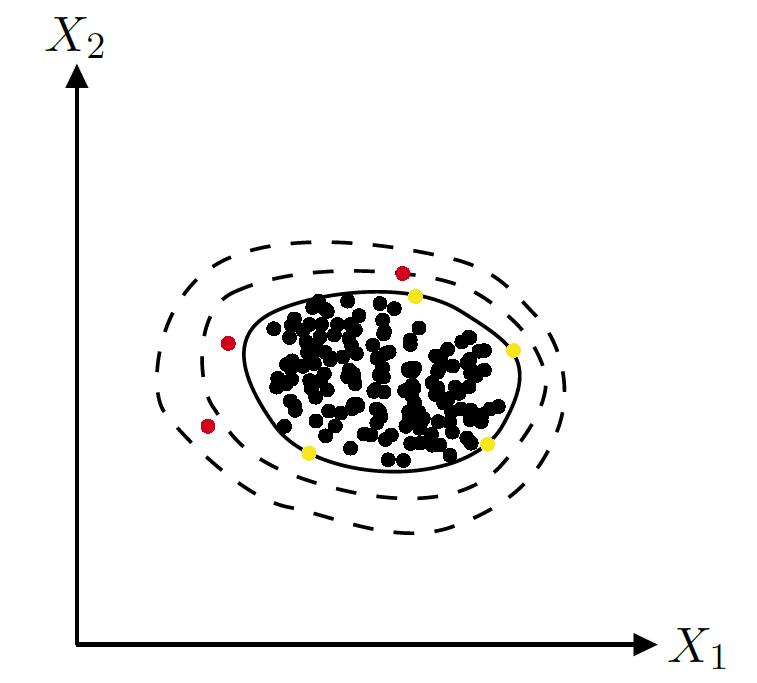
An approach to this that is wildly used is that of environmental contours, as shown above for a bivariate case. They aim to encompass a set of possible combinations of the variables that correspond to a desired return level. A return level describes the value we expect to see with a certain frequency. For example, the inner contour could respresent the 100th return level, that is, any value outside of the contour is expected to occur fewer than every 100 observations. The estimation of these contours is a complex and developing problem, one of great interest to me personally.
Determining the Dependence
In any multivariate setting it is not enough to only determine how each variable behaves; we must also consider how the variables interact with each other. In the case of extreme value theory, we focus on the interaction between
variables in extreme cases. To be specific: how does one variable being large affect other variables’ chances
to be large? Many applications motivate the modelling of these dependencies. Sea walls may be able
to withstand an unusually high sea level or wave height individually, but not simultaneously. Assuming
independence between these two phenomena would lead to an underestimation of the probability of them
being extreme together, and thus an underestimation of the risk of wall failure and subsequent flooding.

For this reason, it is crucial to be able to reliably assess the extremal dependence structure of variables; that is, what does the dependence look like in the joint tail of the multivariate distribution. Much work has gone into the study of this with broadly varying approaches existing. My next blog will take a look at some of these approaches and the motivation behind them.
Before then, I’d recommend looking at this paper if you are interested in the some of the fundamentals of multivariate extremes.
