A different approach
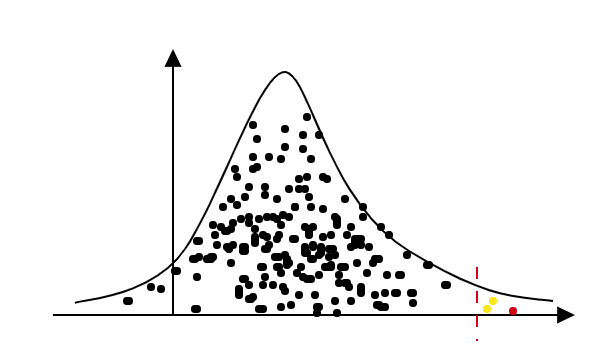
As I covered in my last blog, the block maxima approach to considering extremes can sometimes leading to wasted, or misleading, data. Luckily, an alternative option is available, that of threshold exceedances. Instead of taking maximums of different blocks of data, we can consider all of the data above a certain value, or threshold. For example, now we would also look at the yellow points in the plot below, rather than just the red.
The Generalised Pareto Distribution
With this idea, we now need a model for the observations that occur past the red line. This is given in the form of the generalised Pareto distribution, or GPD. For a random variable X, if we condition on X being greater than some large value u, the distribution of y = X-u is approximately
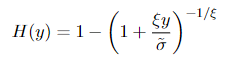
with parameters relating to the parameters of the GEV discussed in my previous post via
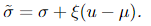
How big is big?

The method poses an equivalent question to that of block size in the block maxima approach; how do we select a high threshold u to model the exceedances of? There is a trade off analogous to that for selecting block size in the block maxima case. Too low a threshold could invalidate the assumptions of the GPD, or one too high could leave not enough data to provide estimates with reasonable certainty. For this reason, much effort has been devoted to the idea of threshold selection.
One of the more simple methods is to re-parameterise the GPD shown above, so that its parameters are not dependent on the threshold u. Then, maximum likelihood is used to find estimates for the new parameters for various thresholds, and the lowest for which the appear to be stabalising is selected. This maximises the amount of data available whilst also appearing satisfying the conditions for the model to be valid.
There are other, more involved, ways of calculating a suitable threshold, such as mean residual life plots. These, as well as an outline of the theory behind the GPD, are discussed again in this book. In my next post, I will explore ideas beyond the contents of this book, however, with an introduction to multivariate extreme value theory.
