Families, Farms and Fission

Galton and Watson

In Victorian England, people became concerned that aristocratic surnames were begining to die out. So, in 1873, Sir Francis Galton asked how likely a surname is to go extinct within a region. The orginal question, submitted to The Educational Times, is shown below.

The gist of this is – “What is the percentage chance that a family name will have died out after a certain number of generations?”. Together with Rev. Henry Watson he went on to publish a paper in 1874 which introduced the Galton-Watson Process.

The Galton-Watson Process is a type of Branching Process, an area of probability used to model systems that evolve randomly over time. By making some simplifications about how a family reproduces, we can use probability theory to model the future of the family lineage and thus find how likely it is that the family will die out and their surname go extinct.

Galton and Watson assumed that the number of children each family member has isn’t affected by the number of children another has. So, if someone has a particularly unappealing sibling, this doesn’t affect their chances of reproducing. They also assumed that each family member has the same chance to have a given number of children. In probabilistic terms, this means that the numbers of children for each family member are independently, indentically distributed. Also, for the sake of the surnames context, they assume that any marriage to an individual in the family results in the transmition of the family surname.

Using this model, they were able to find interesting and useful results. For example they showed that, if the expected number of children for each family member is \mu , then the expected size of the n^\text{th} generation is \mu^n .

Crucial to the orginal question, they also determined in which situations the family would die out. If \mu \leq 1 , then the family is guaranteed to die out and the surname become extinct. However, if \mu > 1 , then there is a chance this family lineage will continue indefinitely. Determining this probability requires knowledge of generating functions, an area of mathematics often useful in the field of probabiliy. If you are interested in an informal, graphical explanation of how this is done see my report Branching Processes and their Applications.

More Applications

The theory of Branching Processes is not limited in application to the survival of family surnames. Any problem which can be thought of in an way equivalent to Galton and Watson’s model is suitable for analysis by this method. For example, consider a farmer who is interested in the genetic mutation of their crops. Say that a mutant gene appears in a single plant; we consider this to be equivlant to the first (or current) generation of the family. We can then consider each plant’s ‘children’ to be the number of its offspring that contain the mutant gene. The results described above can then be used to determine if the mutant gene will die out (i.e. results in non-beneficial traits) or has a chance to persist (provides an advantage for the plant).

Another application is to the modelling of nuclear fission reactions, such as those in nuclear reactors and atomic bombs. Nuclear fission occurs when a neutron collides with a large nuclei, causing it to split into two (or more) smaller nuclei and release energy. This process also releases more neutrons which can then collide with other larger nuclei, causing a chain reaction. A diagram of this process is included below.

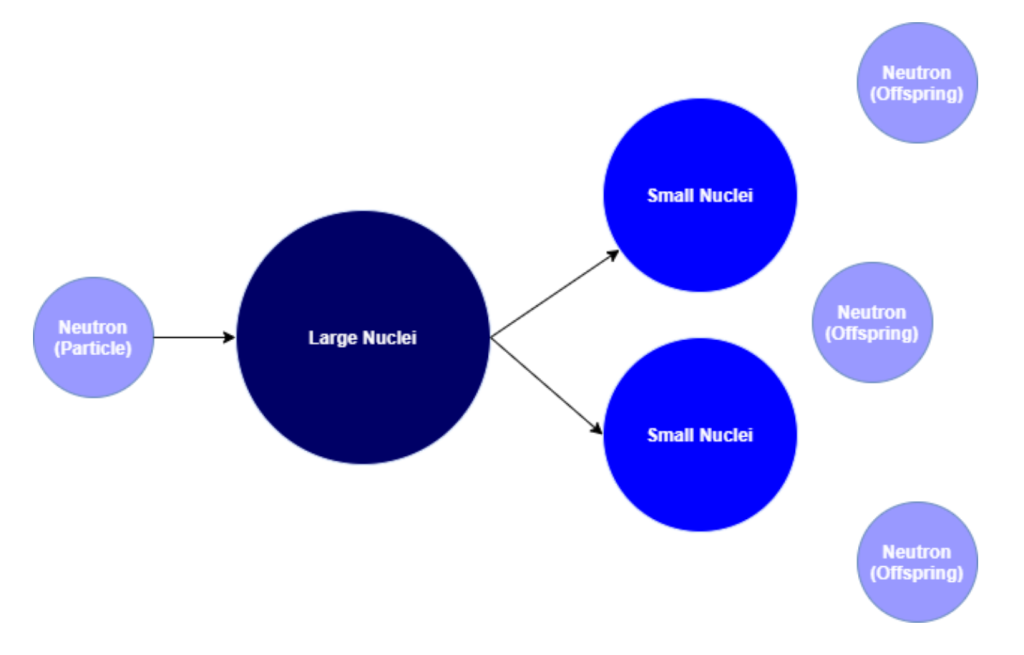
To apply our theory to this example, we focus on the neutrons (or particles). These are equivalent to the family members and their children (or offspring). The notion of a generation corresponds to a ‘era’ of neutrons, each era consisting of the neutrons released from collisions involving the neutrons of the previous generation. That is, if the n^\text{th} generation of neutrons results in collisions which release m neutrons, these m neutrons will form the (n+1)^\text{th} generation. The physics is simplied here and we assume that each collision will always produce the same number of offspring, say k , and that each neutron has the same chance of causing a collision. This way, the probability of a collision is equivalent to each neutron producing k offspring, with the probability of zero offspring being the probability that there is no collision.

Under these assumptions, the fission model fits the requirements to be described by the Galton-Watson Process. We can then make deductions about the evolution of the fission reaction. For example, we could take \mu \leq 1 to mean a controlled reaction to which more fuel would eventually need to be added, such as in a reactor. Alternatively, \mu > 1 could indicate an uncontrolled reaction or an explosive, like an atomic bomb.

Limitations

Of course, all the applications discussed here require us to simplify the problems considerably. It is reasonable to say that the number children a person has could be influenced socially by the number their parents had. You could argue too that if their sibling has had success reproducing, their shared genetics would result in them having an increased likelihood of success. Also, many assumptions about nuclear fission have been made that do not hold in reality. However, this disconnect between theory and practice is present in any mathematical model – but it does not mean it is a bad one. Simple models like this with strong theoretical results can give us a preliminary idea of how the real world works. Plus, they are often detailed enough to provide surprisingly reliable predictions.

If you are interested in reading more on the topic, please see these books;
• Introduction to Probability Theory and its Applications – W. Feller,
• The Theory of Branching Processes – T. Harris.