Recently, I published blog post introducing the concept of heuristic search, this can be found here. Which was followed up with a discussion linear space search methods, in particular branch and bound, which can be found here. This blog is a continuation of these, in which some selective search methods will be discussed.
In order to solve very complicated combinatorial optimisation problems, in particular ones in which it is not possible to guarantee the quality of solutions found, selective search methods can be used. All search methods considered up to this point have been based around a systematic search of the solution space, and the methods involving heuristics increased the speed of the search process in order to reach the goal more quickly. As they all take the complete search space into account, they should all find the optimal solution. In addition to this, the previously addressed approaches have been deterministic, they will always give the same result every time they are performs on the same problem. Search methods discussed here have elements of randomness involved in them. Randomised heuristic search methods can be catagorised as either a Las Vegas algorithm, which always yields the optimal solution, however takes a variable amount of time, and Monte Carlo methods, which only sometimes yield the optimal solution.
Selective search is a generic term, which includes attributed from both local and randomised search. Selective search methods as said to be satisficing, meaning that they may not always output the optimal solution, although they may by chance, yet should still yield a very good when implemented correctly
Hill Climbing
Hill climbing is an example of a local search method. Local search is applied widely in combinatorial optimisation. The aim of local search methods is the optimisation of an objective function in a local neighbourhood of states in a solution space, with the aim of finding a solution which is approximately globally optimal. This type of algorithm does not search the entire solution space, hence they aim to find a solution which is more optimal than the other states in its neighbourhood. Selective search methods can be used to modify the size of steps in the solution space, in order to tune the process and alter the size of the neighbourhood being explored at the cost of optimality.
Hill climbing first selects uses an evaluation function in order to select a neighbourhood in which the optimal solution is likely to be located, and searches the solution space here. Hill climbing (for maximisation) and gradient descent (the equivalent for minimisation) aims to make changes which improve the objective function until it is no longer possible to improve it. This is often done in one of two ways, the first is that all neighbours to the current solution are checked, and the one which offers the greatest improvement is chosen, this is known as simple hill climbing. The other by proposing a change to the solution at random, and accepting the change if it results in the objective function improving, and rejecting the change if it does not, this is known as stochastic hill climbing.

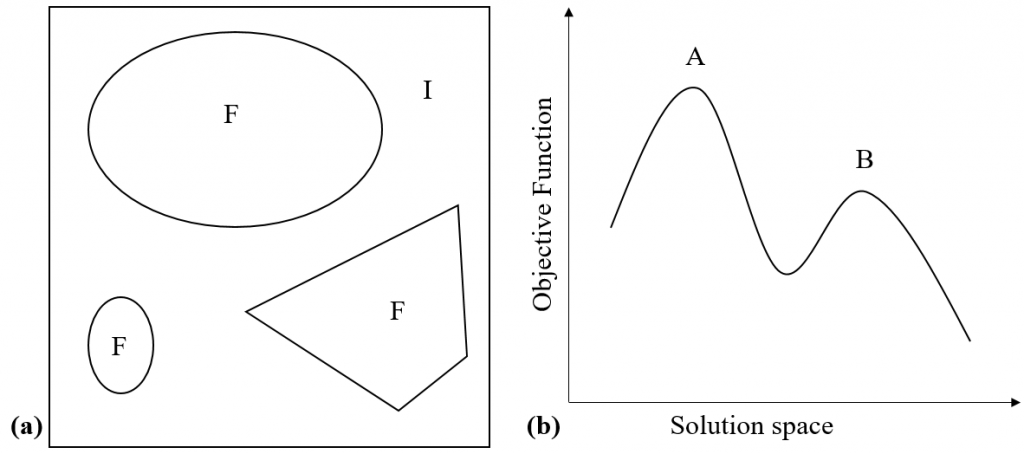
There are issues associated with hill climb methods. First is the issue that some proposed changes may result in an infeasible solution that violates the constraints of problem, which is prevalent when the solution space has regions which are both feasible and infeasible regions as seen in figure (a) below (where F represents the disconnected feasible region and I represents the infeasible region). Second is the obvious issue that the local optimum may not be globally optimal and may in fact be very far way, such as for the solution space shown with the objective function in figure (b) below (where A is the global maximum but B is a local maximum). This places importance on choosing where the hill climb starts, however there is often not much information available about the locations of local maxima, so a random start point is often chosen.
Simulated Annealing
Simulated annealing is a search method based on an analogy of the process of annealing in metallurgy, it can be viewed as a development of a stochastic hill climb. The process of annealing involves the heating a material above a certain threshold temperature, maintaining this temperature for some time, then cooling it in order to alter the properties of the material.

This algorithm is effectively a form of Metropolis Hastings. The algorithm generates a new state by perturbing the current state using a small, random change to move the sate of the solution in the solution space. In metallurgy this algorithm is used to simulate the cooling part of the annealing process, here the objective function, represents the total energy of the material. If the energy of the material in the proposed state is less than that of the current state, then the move is accepted. If it is not, then the move is accepted with a probability according to a Boltzmann distribution. The reason for this is based on the physics of the annealing process. In statistical thermodynamics energy changes at a certain temperature are distributed according to a Boltzmann distribution. Over time, the temperature is decreased, to simulate the material cooling. A high energy material will make bigger jumps in its state space, whereas a cooler one will make smaller jumps, hence the gradual cooling will allow a coarse energy minimisation to start with (as a lot of unfavourable moves will be accepted) as the algorithm effectively selects a neighbourhood of states and the the minimisation gradually becomes more and more local. This allows the material to cool to its minimum energy state whilst attempting to avoid energy traps (local minima in its energy landscape). It should be noted however that slower cooling will result in an increased computational cost.
This translates to a general combinatorial optimisation problem by considering an general objective function which is to be minimised, and a tuning parameter (in place of temperature) which is gradually reduced. Application of this method allows for a coarse optimisation at the start of the problem, effectively choosing the neighbourhood to search in, which tends towards being a more and more local search as time goes on. In theory this should avoid local minima, such as the one shown in figure (b) above, however due to the randomness in the method it still may become stuck in a local minimum, but this is considerably less likely than with a stochastic hill climb.
About the author
