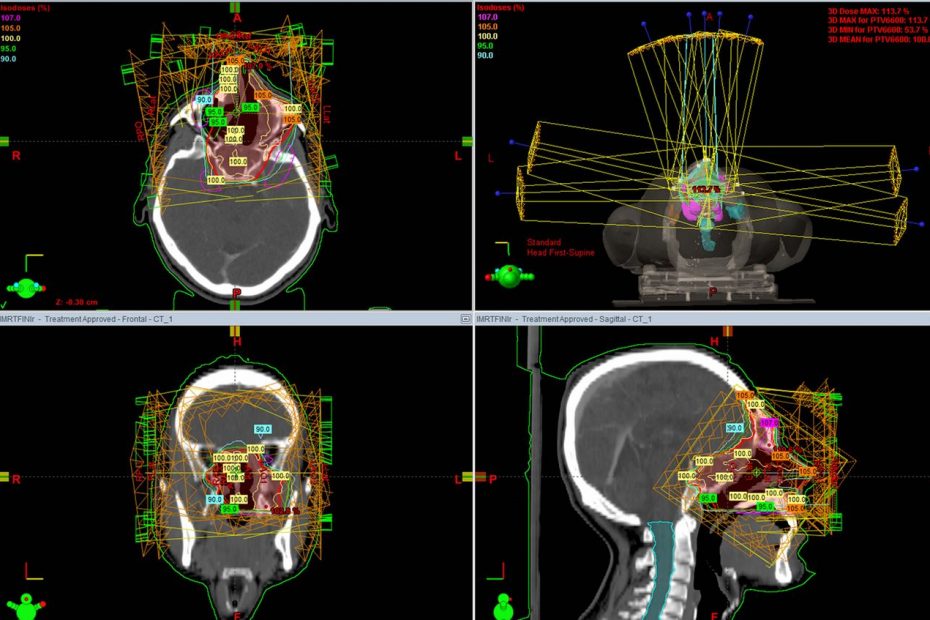
This post is part of series about IMRT Planning, if you haven’t read the introduction to this series you can find it here. This blog series was inspired by the research I did as part of STOR601.
What is the problem?
The first part of IMRT that needs to be determined are the angles that the radiation is delivered from the accelerator. For patient comfort the number of angles is normally limited (more angles, longer treatment) so three to nine different angles are used.
Traditionally, these are selected by a clinician based on experience but mathematical optimisation has shown that sometimes unintuitive angles can be optimal. The process of determining an optimal (or near optimal) group of angles to use is called Beam Angle Optimization or BAO.
What are the challenges?
One challenge with selecting the angles is that there are infinitely many angles to choose from. The linear accelerator providing the radiation can rotate a full 360 degrees about a point, known as the isocentre. This means it is impossible to try every conceivable combination of angles to find the best set.
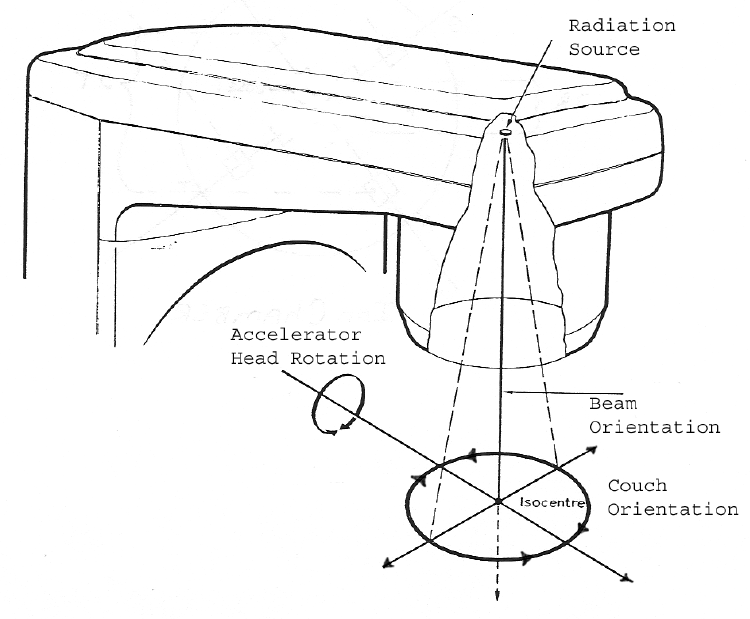
It can be argued that if two angles are sufficiently close together then there is no difference to which one is chosen. Therefore, it is not necessary to consider infinitely many angles but choose n angles from a pool of m equally spaced angles. For example, choose eight angles from the following set of angles:
\{0^\circ,10^\circ,20^\circ,\dots,350^\circ\}.
This helps reduce the number of angles considered but has it been reduced enough. In our example above there are over 30 million ways to choose 8 different angles from a pool of 36 angles (precisely 30,260,340 combinations).
Another challenge with selecting the angles to use is that there needs to be a way of evaluating this choice of angles before treatment. This is so it is possible to compare two different groups of angles and deciding which group is better. It also provides a way of deriving gradient based searches to find locally optimal groups of angles
Normally a simplified version of the next phase, Fluence Map Optimization, is used. Given a group of angles, it is possible to get a number relating to the quality of the treatment, or to find how this number changes as the chosen angles change slightly.
More precisely, for a given group of angles an optimisation problem is solved and the resulting objective value is compared with objective values from different groups of angles. Alternatively, the gradient of the objective function with respect the the angles can be found, allowing us to start with a group of angles and iteratively adjust these angles to move towards a better objective value.
What is the next step?
The next step in this process to solve the Fluence Map Optimization problem in full. The simplified versions solved above to evaluate a group of angles are not accurate enough to to be used in practice.
Read about the challenges of Fluence Map Optimization (FMO) here
Further Reading
BAO problem solved using an “exhaustive search” strategy
BAO problem solved using a local gradient search method
BAO solved using a hybrid method, combining gradient search with simulated annealing