STOR-i Masterclass: Professor Peter Frazier

This week we had the last masterclass of the year given by Professor Peter Frazier from Cornell University. Due to the current uncertainty caused by the coronavirus outbreak around the world, unfortunately Peter was not able to visit Lancaster in person. However, making the most of the situation we instead were able to still interact over the internet and it was an interesting half a week.

Peter’s area of expertise is in operations research and machine learning and gave us an introduction to Bayesian optimisation, specifically how we could implement it ourselves using the programming language Python.

The problem motivating Bayesian optimisation is as follows: suppose we have a function which we wish to find a maximum of, but for the purpose of this explanation we do not know what the function is. This is commonly thought of as having a “black box” where we pass in some inputs and get a output without getting to see what happens inside. Thus we can not simply differentiate the function as we might be used to. Furthermore, when estimating our function we may be getting noisy estimates, a common idea is to assume we are adding a \( \mathcal{N} (0,1) \) sample to each evaluation.

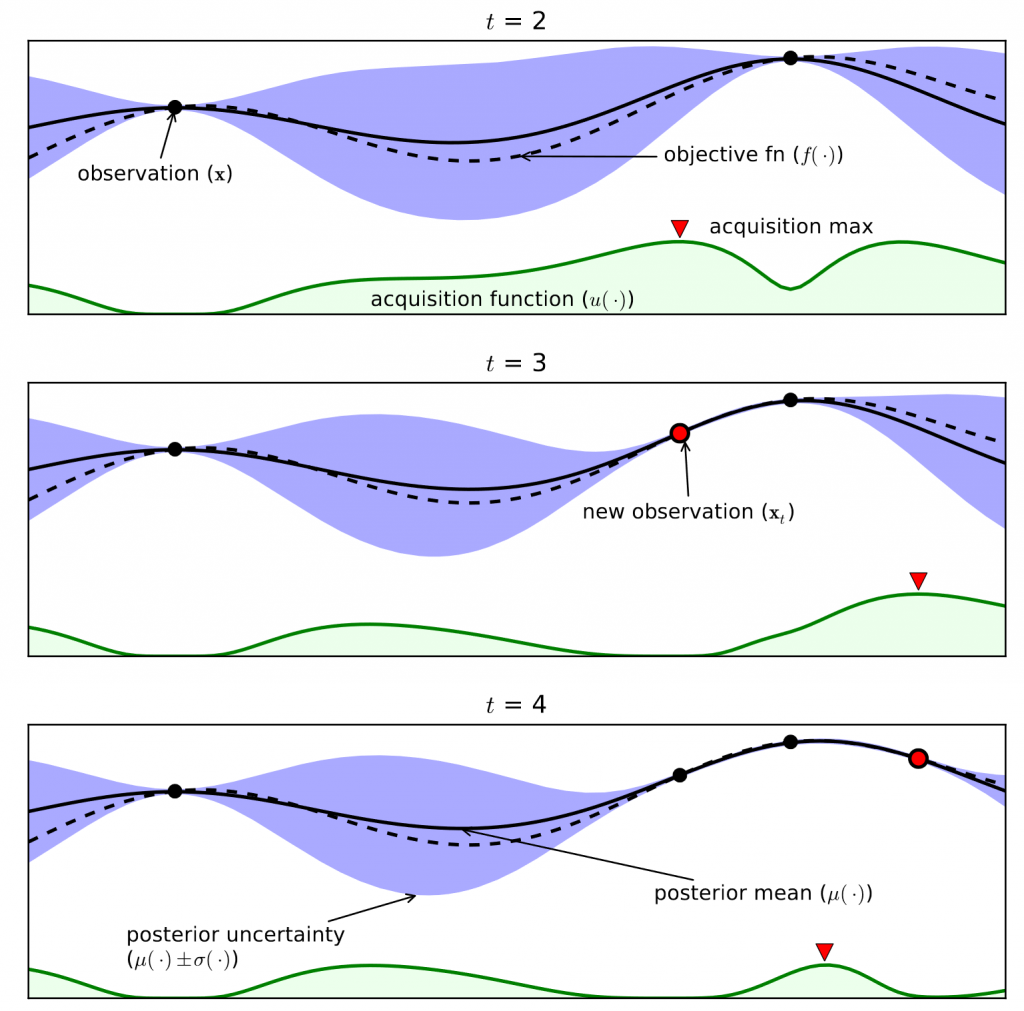
The way Bayesian optimisation tackles this problem is to estimate the function using a Gaussian process. Essentially we consider having a function for the mean of the function, and another for the variance. At each time step we can make one more evaluation of the function, and with each extra data point our Gaussian process becomes a better and better approximation of the “hidden” function.

The complicated part is choosing where we want to choose for our next evaluation. There are two concepts which need to be balanced: exploration and exploitation. Exploration relates to wanting to check over the whole range of the function, not leaving an area undiscovered. Exploitation is if we can see one area is looking better than others, we want to focus looking there to find the global maximum. The methods we learnt to deal with this is by using different functions that take both factors into account, called acquisition functions. We then simply choose the maximum of this for the next location to evaluate.

If you would like to learn more about the topic, Peter has an excellent set of resources on his website.