Back in January, we had talks about different topics of research in the field of statistics, OR or statistics and OR in STOR-i. We were then asked to write two reports in two topics. As you may have guessed by the title, one of the topics I chose was Historical Clinical Trials. In this post, I will explain a bit of the research I did while writing my review report.
What are Clinical Trials?
When there is a new treatment available, we need to evaluate its effect on human health. A way to do so is through Clinical Trials. These are carefully designed and approved before their start and involve usually 4 different phases, each of which with a different purpose.
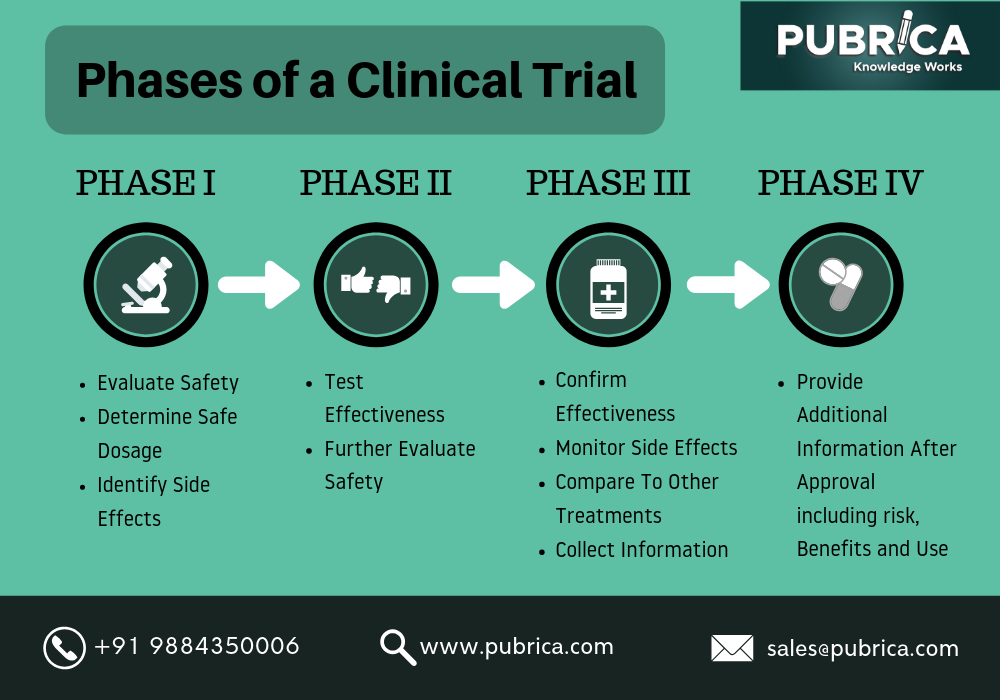
However, these trials can take a long time to reach the end. For example, 10 years may be needed to complete the first 3 phases, which makes these trials expensive. As you can imagine, in situations as the one we have been living in for over a year now, having a trial of 10 years for the development of a vaccine for example, is far from ideal. So, all the ways to reduce the duration of it (and, consequently, the cost of it) are welcome.
For some years now, a way to achieve this goal is by incorporating data that is available from previous trials in the analysis. These types of trials became known as Historical Clinical Trials. In these, patients enrolled in a new treatment are compared with patients which were enrolled in a previous standard treatment (e.g. placebo). Usually, past information is used either in phase I or phase II of the process. Borrowing historical information can have advantages or disadvantages (as everything in life). We can get more efficient clinical trials, and thus reduce time and costs and/or in patients we need. But we can also obtain biased results if the past data doesn’t have similar characteristics to the ones of the trial we are currently doing.
There are several ways for combining the historical data with the current one. For instance, we can ignore the historical data completely, use it all in the analysis or use Hierarchical Models. It is also possible to choose between a frequentist or a Bayesian trial. The latter allows for more flexibility, to model more complex data and/or to include uncertainty and covariates. However, with inconsistent data, these trials can be more expensive and extensive, which is not good.
Hierarchical Models
Hierarchical Models (HMs) assume a distribution across the two data and allow to incorporate uncertainty in the model. They are able to approximately determine, through the consistency between the two sources of information, how much we should borrow. Indeed, the more inconsistent the historical data is with the current one, the less it is used in the analysis.
One application of Bayesian HMs is with survival data. Assume we have H historical trials and N patients. In addition, we have two indicator variables I_i^C, I_j^h specifying whether the patient belongs to the historical control group, to the current control group or to the current active group. So, we have censored data with covariates (X, I_i^C,I_i^h) and the model can be written as
\log(\lambda_i(t))=\log(\lambda_0(t))+\alpha X +\beta_CI_i^C+\sum_{h=1}^{H}\beta_hI_i^h,where \lambda(\cdot) are hazard functions (details about the model can be found in the first paper referenced). The HM for \beta_C and \beta_h is formulated as
\beta_C,\beta_h \sim N(\mu,\tau^2).To implement the model, we have to assign priors to \alpha,\mu,\tau^2 , usually noninformative. It’s precisely the parameter \tau^2 that represents the amount we borrow from the historical information. If it’s small, more we borrow, but if it’s large, less information will be used in the analysis.
Conclusion
There are some advantages on borrowing information from previous trials. In fact, we can achieve more efficient trials. However, there are some concerns. First, it is still not very clear when it’s acceptable to borrow such data and, if so, which method to use. Additionally, when using HMs, we need to choose prior distributions. Although there are a lot of options for clinical data, different priors may lead to different results. It is also important to ensure that the characteristics of the current trial are fairly similar to the ones of the previous trial in order to get valid conclusions.
What now?
In this post, I gave a very brief introduction to this topic. If you are interested, you can find more in the following papers:
- Covariate-Adjusted Borrowing of Historical Control Data in Randomised Clinical Trials by Han et al. 2017
- Increasing the Efficiency of Randomized Trial Estimates via Linear Adjustment for a Prognostic Score by Schuler et al. 2020
I hope you liked this post and hope to see you on the next one!

