The other day I was trying to imagine what my life would have been like if I had chosen to pursue a music degree instead of a maths one in uni (for those who don’t know, I’ve played the piano since I was 6 and I attended a music school for 7 years). While I was thinking about this, I found myself searching about any possible relation between music and statistics or operations research. Surprisingly, I discovered I wasn’t the only one questioning their relation. In fact, I found a quite interesting post written by Dr. Dorien Herremans and Dr. Elaine Chew entitled “The role of operations research in state-of-the-art automatic composition systems: challenges and opportunities”.
Operational Research (OR) can have a lot of applications in health or financial matters but it can also be applied in art fields. For example, Shazam and Spotify based their algorithms in techniques that may be common to OR. Herremans and Chew believe that automatic music generation can be seen as an optimisation problem. Briefly, this is a recent area that aims to create changeable music, mainly relying on human-conceived designs, in scalable ways for more banal scenarios without replacing composers. But how can the generation of music be considered a optimisation problem? For instance, the objective function can be a measure of quality of music subject to satisfaction, i.e., the finding of the correct combination of notes.
Quantifying Quality
Human evaluation is probably the main way to assess music quality but we can also turn to the theory, in order to see if the piece follows certain rules, or, most recently, to machine learning. In reality, the objective function will be constructed using machine learning techniques. In their studies, Herremans and Chew developed a system where they integrated Markov models in the objective function of a metaheuristic, a high-level heuristic, to tackle complex polyphonic music (two or more simultaneous lines of independent melody) and to detect recurrent patterns.
Music Representation
The next step of defining the problem is to know how to represent music. If we think about it, music is nothing more than a combination of notes, which in turn have properties such as the pitch, duration, etc. So, we may think of a mathematical representation for music. For their proposed system, Herremans and Chew tried to find new pitches, satisfying constraints given an extracted rhythm template from an existing piece. This way, they could alter the pre-existent piece into a new composition. Without getting into detail, a spiral array model for tonality was used, where pitch classes, chords and keys were represented by helices, as shown below.
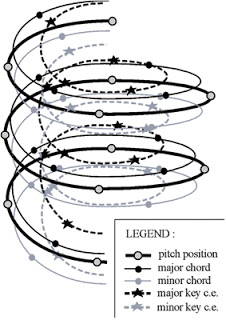
Then, chords and keys would be generated as combinations of their defining elements: tonic, subdominant and dominant.
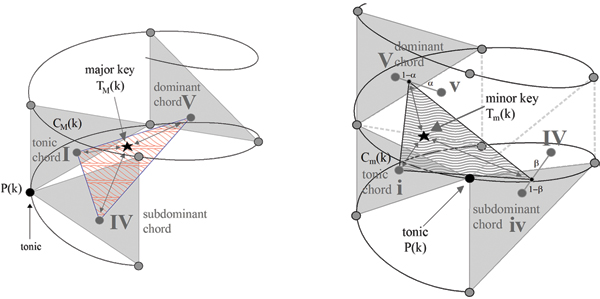
Detecting Music Patterns
Finally, the system developed by Herremans and Chew not only had the goal of recreating the palpable tension which music generates but also aimed to detect recurrent patterns. It’s non-arguable that repetitions play an important aspect in a music piece. So, the authors wanted to generate patterns with the same length and placed them at the same time as in the original piece. But, for that, they needed to find the patterns on the original piece first. Thus, they recurred to compression algorithms.
Summarising, Herremans and Chew defined music generation as an optimisation problem. They consider a template piece and extracted its rhythm structure. Then, their method finds a new pitch for each note and alters the original piece into a new one. Finally, the patterns found with compression algorithms are used to form additional constraints during the optimisation problem in order to ensure some coherence. Their end goal is to generate music with a specific tension profile.
What to conclude?
Although the system proposed is able to generate a piece of music, some problems arise. First of all, music created by these types of systems won’t take into consideration the playability of the piece, for example, if it contains impossible sequences to play (such as difficult hand crossings or huge leaps). They also won’t account for the emotion that a piece composed by a human being usually has or for necessities the artist has when playing, e.g. having a pause to breathe.
Nonetheless, I found this research interesting as I had never thought of music composition as an optimisation problem. For a deep comprehension of the topic, please visit the original post in Elaine Chew’s website.
Thanks for reading, see you soon!

