My my last blog post focused on how to analyse a single clinical trial with multiple treatment arms. But what if we want to consider results for multiple trials studying a similar treatment effect?
During my research for my MSci dissertation (see the last blog post to find out the basics of my research) I came across the concept of meta-analysis. The overall motivation for conducting meta-analyses is to draw more reliable and precise conclusions on the effect of a treatment. In this blog post I will outline for you both the benefits and costs of conducting a meta-analysis.
Meta-analysis is a statistical method used to merge findings of single, independent studies that investigate the same or similar clinical problem [Shorten (2013)]. Each of these studies should have been carried out using similar procedures, methods and conditions. Data from the individual trials are collected and we calculate a pooled estimate (although data is not usually pooled!) of the treatment effect to determine efficacy.
Effectiveness vs. Efficacy: ‘Efficacy can be defined as the performance of an intervention under ideal and controlled circumstance, whereas effectiveness refers to its performance under real-world conditions.’ [Singal, A. et al. (2014)].
If conducted correctly, efficacy conclusions from a meta-analysis should be more powerful due to the larger sample size created by considering several studies. Often this sample size is far greater than what we could feasibly achieve in a single clinical trial, which is constraint by funds and resources including the availability of patients. This increased sample size also improves the precision of our estimate in terms of how closely the trial results relate to effectiveness in the whole population [Moore (2012)].
Although meta-analysis can be a useful tool to increase sample size and hence statistical power, it does have significant associated methodological issues. The first of these is publication bias. This may be introduced because trials which show significant results in favor of a new treatment are more likely to be published than those which are inconclusive or favor the standard treatment. Another form of publication bias arises when researchers exclude studies that are not published in English [Walker et al. (2008)]. This exclusion of studies may lead to an over/under-estimate of the true treatment effect.
The issue of publication bias in a meta-analysis exploring the effects of breastfeeding on children’s IQ scores was discussed by Ritchie (2017). A funnel plot of the original data set showed a tendency for larger studies to show a smaller treatment effect, indicating publication bias. The original study found that breastfed children had IQ scores that were on average, 3.44 points higher than non-breastfed children. However, after adjusting for publication bias a much lower estimate of 1.38 points higher IQ was given. Although this is still a significant result, this example highlights the issue of overestimation resulting from publication bias.
Funnel Plots: A funnel plot is a method used to assess the role of publication bias. It is a plot of sample size versus treatment effects. As the sample size increases, the effect size is likely to converge to the true effect size [Lee, (2012)]. We will obviously have a scatter of points surrounding this true effect size, however, if we have publication bias, we may have a lack of ‘small effect size’ small studies included in the meta-analysis. This will lead to the funnel plot being skewed.
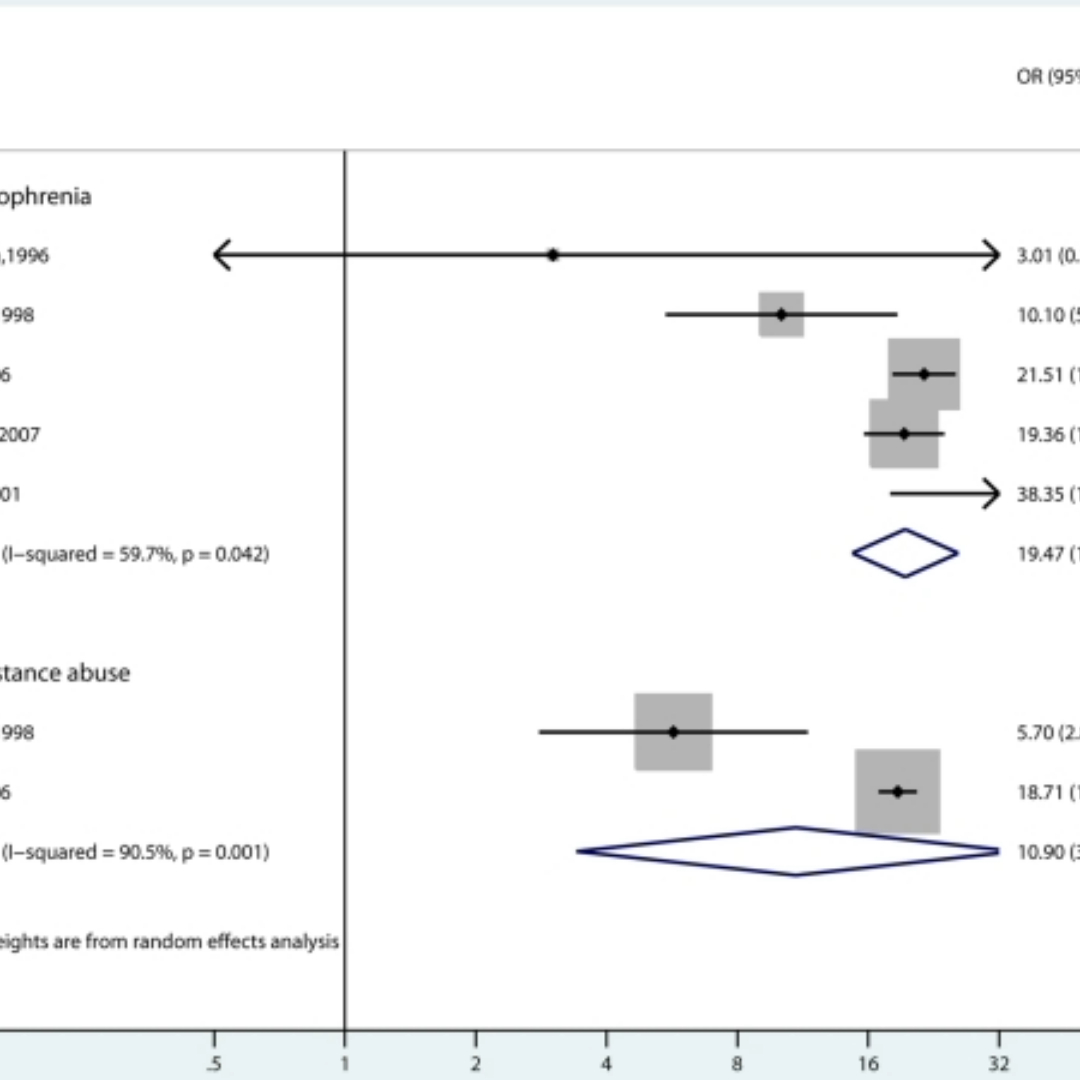
Another key issue with meta-analysis is heterogeneity. This is defined as the variation in results between studies included in the analysis. Investigators must consider the source of this inconsistency, they may include differences in trial design, study population or inclusion/exclusion criteria between trials but also differences due to chance. High levels of heterogeneity comprises the justification for meta-analysis, as grouping together studies whose results vary greatly will give a questionable pooled treatment effect, thus reducing our confidence in making recommendations about treatments. There are methods to handle heterogeneity, one of which is to fit a random effects model.
A meta-analysis considering strategies to prevent falls and fractures in hospitals and care homes [Oliver et al. (2007)] obtained strong evidence to suggest heterogeneity between studies. This variation was highlighted in forest plots which showed a very wide spread of results. As the investigators believed all trials were similar enough in design and all aimed to trial the same treatment, they felt it was justified to calculate a pooled treatment effect. However, this high variability brings into question the reliability of the estimate, complicating decisions regarding recommendation of treatments.
In summary, Meta-analysis is a very useful tool for combining results of studies in order to boost the precision of our conclusions. We do however need to proceed with caution and ensure heterogeneity and check for publication bias.
References & Further Reading
- Lee, W., Hotopf, M., (2012). Critical appraisal: Reviewing scientific evidence and reading academic papers. Core Psychiatry, 131-142.
- Moore, Z. (2012). Meta-analysis in context. Journal of Clinical Nursing, 21(19):2798-2807.
- Oliver, D., Connelly, J. B., Victor, C. R., Shaw, F. E., Whitehead, A., Genc, Y., Vanoli, A., Martin, F. C., and Gonsey, M. A. (2007). Strategies to prevent falls and fractures in hospitals and care homes and effect of cognitive impairment: systematic review and meta-analyses. BMJ, 334(7584).
- Ritchie, S. J. (2017). Publication bias in a recent meta-analysis on breastfeeding and IQ. Acta Paediatrica, 106(2):345-345.
- Singal, A., Higgins, P., Waljee, A. (2014). A primer on effectiveness and efficacy trials. Clinical and Translational Gastroenterology, 5(1).
- Shorten, A. (2013). What is meta-analysis? Evidence Based Nursing, 16(1).
- Walker, E., Hernandez, A., and Kattan, M. (2008). Meta-analysis: Its strengths and limitations. Cleveland Clinic Journal Of Medicine, 75(6):431-439.