We are currently choosing our PhD project preferences and as they thought it might be useful, this week the MRes students were kindly invited to join the Networks reading group for a session which was an intro to Hypergraphs. Personally, I hadn’t come across hypergraphs before and I can really see the benefits of them. One of the PhD students, Amiee Rice, gave a great overview based on a paper (see references below). I had never considered how much information is clearly missing on a normal graph in some situations and hypergraphs are great ways to represent this information more accurately.
If you have never come across graph theory before, check out my previous blog post Graph Theory 101 for the basics.
What is a hypergraph?
We have a set of vertices \(V\) and hyper-edges \(E\) and a hypergraph is represented as a combination of these \(H = (V,\,E)\), much like in a graph. However where as in a graph, an edge can only connect 2 vertices, in a hypergraph an edge can connect multiple vertices. For this reason they are often represented using a loop around all the vertices connected by the edge rather than a line connecting each edge.
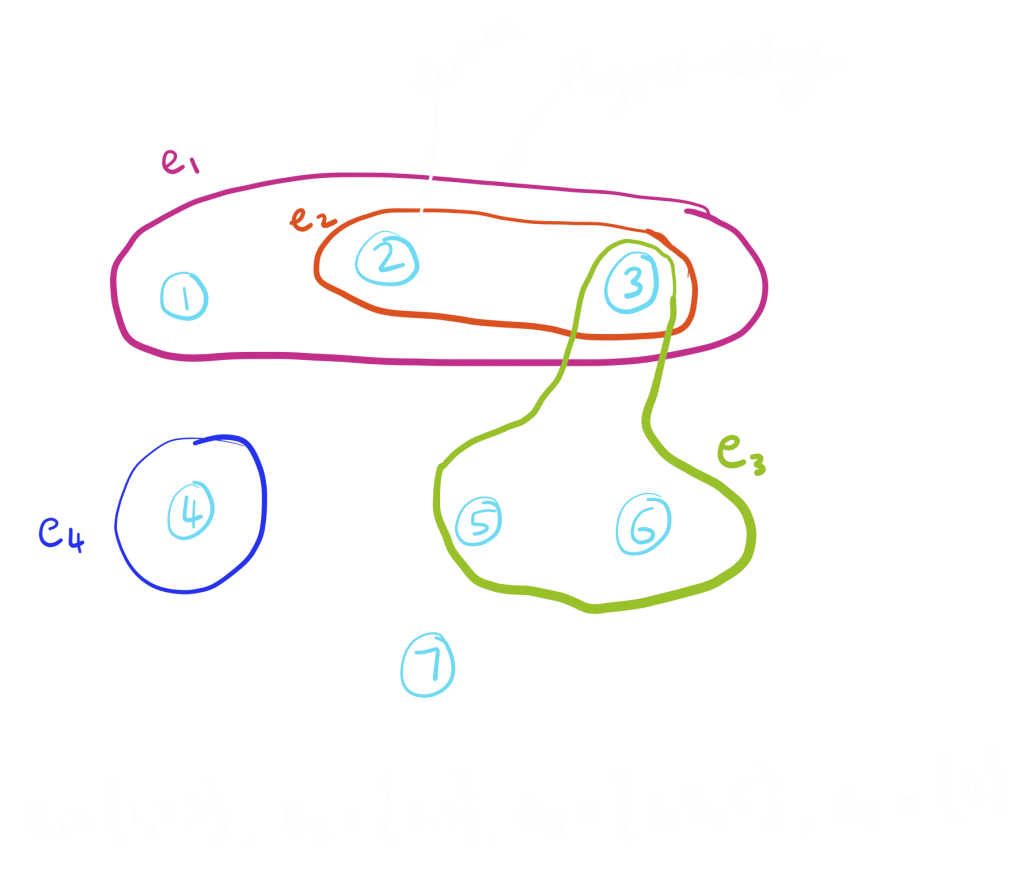
The use of hypergraphs means we can display information about relationships that feature more than one object. For instance, the example Amiee gave was co-authorship, where we have a graph that represents authors of papers and when they collaberated together on a paper. Imagine have 3 authors A, B and C and the following graph, with the authors as the vertices and the edges representing collaboration on a paper.
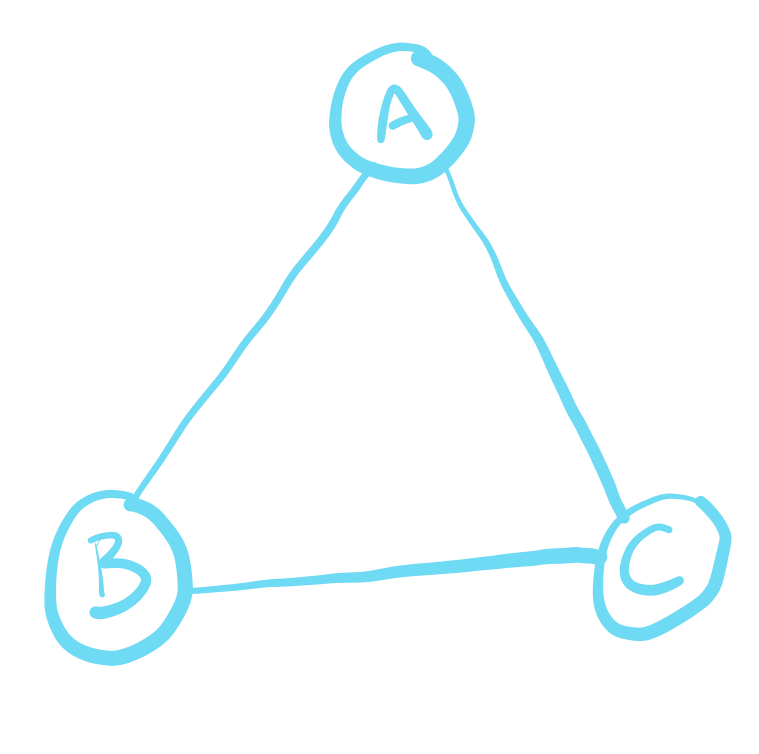
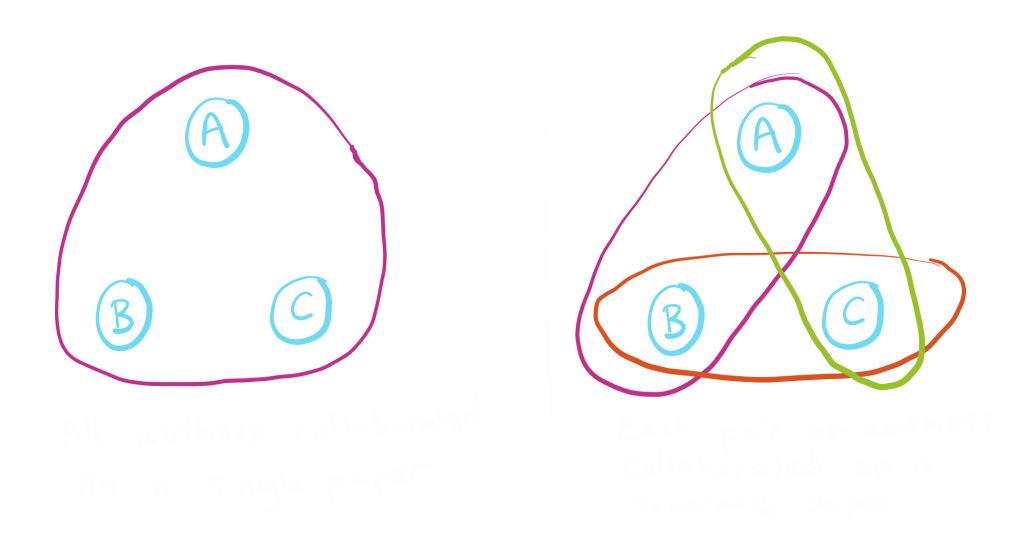
While from this we know each author collaborated with both of the other authors at some point on a paper, we cannot determine if this was seperately on 3 different papers or perhaps all together on a single paper. We can however represent this in a hypergraph where the edge represents all the distinct collaborations on a single paper.
Just like with graphs, we can represent a hypergraph using an incidence matrix with the edges represented by the columns and the vertices as the rows.
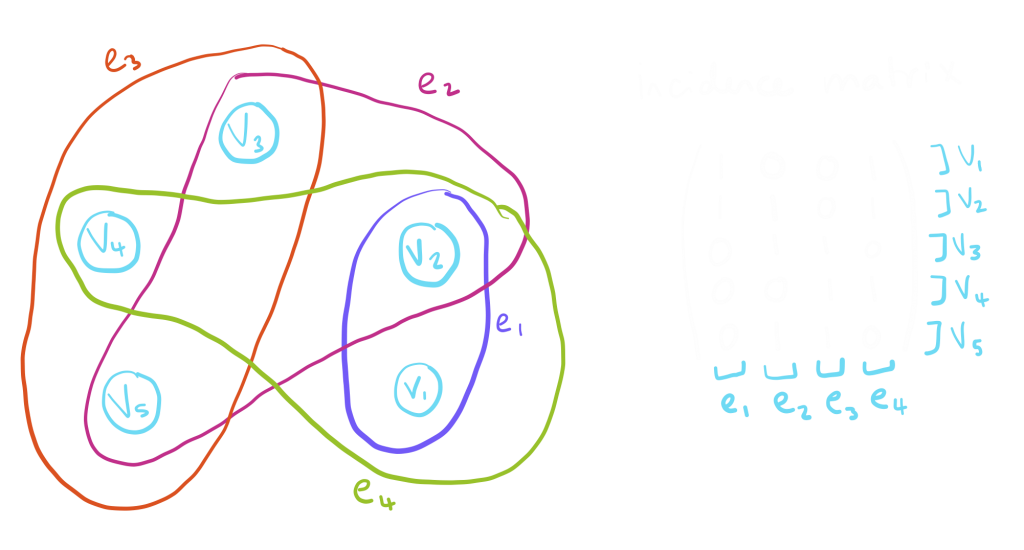
We can also represent a hypergraph using a bipartite graph by making the hyper-edges into a separate set of vertices. This is sometimes referred to as an incidence graph.
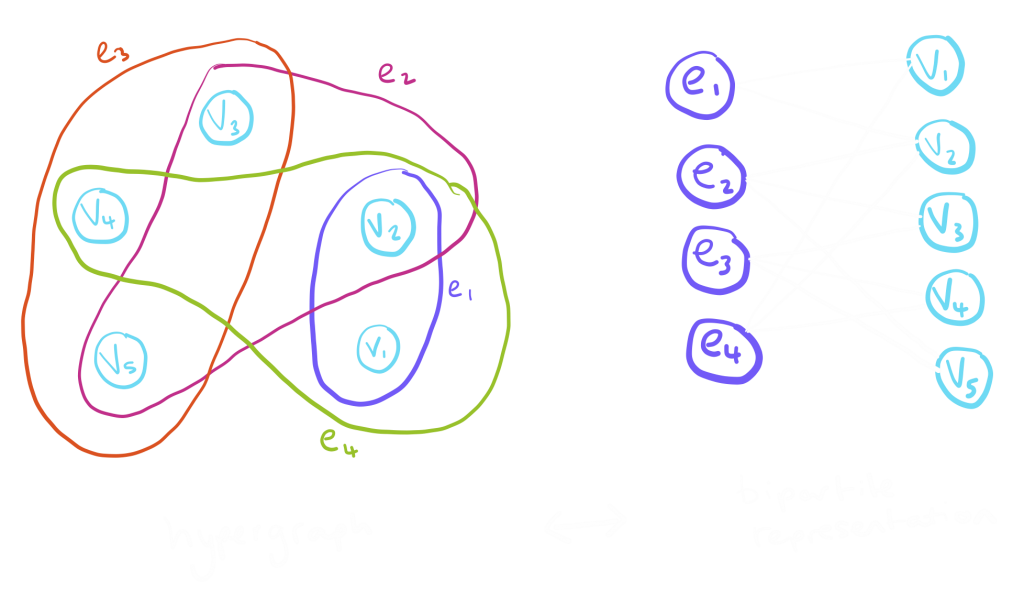
A lot of the graph theory terminolgy is similar for hypergraphs also. Examples of the basics are:
- A path is an alternating sequence of distinct vertices and hyper-edges. Start with an inital vertex \(v_1\) and then move to another vertex \(v_2\) within the hyper-edge they are both contained in \(e_1\), then move to another vertex \(v_3\) within a different hyper-edge \(e_2\) that the vertex \(v_2\) is also connected to and so on.
- A cycle is a path that starts and ends on the same vertex.
- The degree of a vertex is the number of hyper-edge it is contained in.
- We call a hypergraph r-uniform if each vertex has degree \(r\).
- A hypergraph is simple if no edges contain other edges as a subset. So if you had two edges on a hypergraph \(e_1=(v_1,v_2)\) and \(e_2=(v_1,v_2, v_3)\) then this would not be simple because \(e_1\) is a subset of \(e_2\).
- A hypergraph is connected if, for any two vertices, there exists a path between them.
- A k-complete hypergraph is a r-uniform hypergraph where, for each set of \(k\) vertices, there is a distinct hyper-edge containing those \(k\) vertices. We may refer to it as just complete if it is k-complete for some \(k\).
Examples of use
Recommender systems, for example, music recommendation such as in this paper Using rich social media information for music recommendation via hypergraph model (psu.edu). In the paper, they model the recommendation problem as a ranking problem on a unified hypergraph. A unified hypergraph is a hypergraph that has vertices and hyperedges that can be of different types (for example, some vertices represent users and some vertices represent songs). They propose an algorithm that creates music recommendations using this type of hypergraph. The hyper-edges are relations among objects in a music social community, one set of such hyperedges are similarities in tracks based on acoustic signals. While the vertices are these objects in a music social community themselves.
Image retrieval searching and retrieving images from a databases of images. The following paper again uses a unified hypergraph with images as vertices and different types of relations in individual modality are different types of hyper-edges, that is things such as image content, user-generated tags and geo-locations. UNIFIED HYPERGRAPH FOR IMAGE RANKING IN A MULTIMODAL CONTEXT (ucsb.edu)
Competition networks a hypergraph can be used to indicate competition within the food chain. Different species are the vertices and those that are in competition for a certain type of food (this food is usually another species) are contained within the same edge. This is included in the Complex Networks as Hypergraphs paper linked in the references below.
References
Complex Networks as Hypergraphs – Ernesto Estrada, Juan A. Rodriguez-Velazquez Complex Networks as Hypergraphs (arxiv.org)
Voloshin, V. (2009). Introduction to graph and hypergraph theory. Hauppauge, N.Y.: Nova Science.
1 thought on “Hypergraphs – not just a cool name!”
Comments are closed.