Imagine you have a sample of data and you wish to calculate the mean. Now you can easily calculate the sample mean, but how do you know if that is indicative of the population mean or not? In a perfect world you could gather a much much larger sample including the entire population and accurately calculate this however in a lot of cases this is not possible and the original sample is all you’ve got. In this case we can use a technique known as bootstrapping.
What is bootstrapping?
Bootstrapping is repeatedly taking a random sample from your available sample (with replacement so you may sample the same data many times). On each iteration you select a random sample of a chosen size (often the same size as your original sample) and repeat this for many iterations. You can then calculate various parameters estimates for each sample and use the distribution of these to create a confidence interval. Bootstrapping is useful for non-parametric distributions where it may be difficult to calculate these otherwise.

Advantages and Disadvantages
Obviously bootstrapping is incredibly simple, it doesn’t involve any complex calculations or test statistics. You can use bootstrapping on much smaller sample sizes than traditional statistical methods (even sample sizes as small as 10 in some cases).
A key advantage is that bootstrapping doesn’t need you to make any assumptions about the data (such as normality), regardless of the distribution of the data you still bootstrap the data the same way and all you are using is the information you actually have. Using traditional methods, if you assumptions are at all wrong this can mean that the estimates you get are extremely far from the true values so bootstrapping can be more reliable in this case. That being said not all distributions will give accurate confidence intervals for parameter estimates when bootstrapping. Examples of situations where bootstrapping may fail are with distributions with high correlation or Cauchy distributions (which have no mean anyway).
Testing bootstrapping?
Here I’ve randomly generated a 50 values from a standard normal distribution to represent a sample I may take. I know it should have population mean of zero and standard deviation of 1 but if I use the bootstrapping approach will I a good confidence interval for these?
k <- 50
set.seed(666)
sample <- rnorm(k,0,1)
boot_sample_mean <- NULL
boot_sample_sd <- NULL
n <- 10000
for (j in 1:n){
boot_sample <- NULL
for (i in 1:k){
x <- floor(runif(1,1,k+1))
boot_sample <- c(boot_sample, sample[x])
}
boot_sample_mean <- c(boot_sample_mean, mean(boot_sample))
boot_sample_sd <- c(boot_sample_sd, sd(boot_sample))
}Using the code above I’ve created 10,000 new random samples of my original data and stored the mean and standard deviation for these. The 95% confidence intervals I got from this data:
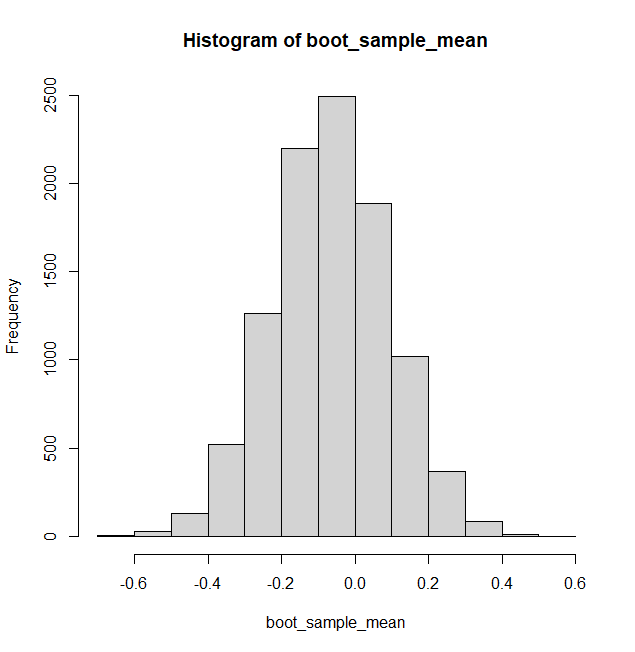
Mean
Bootstrap estimation gives mean of -0.065 with a confidence interval (-0.371, 0.248)
Standard Deviation
Bootstrap estimation gives standard deviation of 1.117 with a confidence interval (0.936, 1.298)
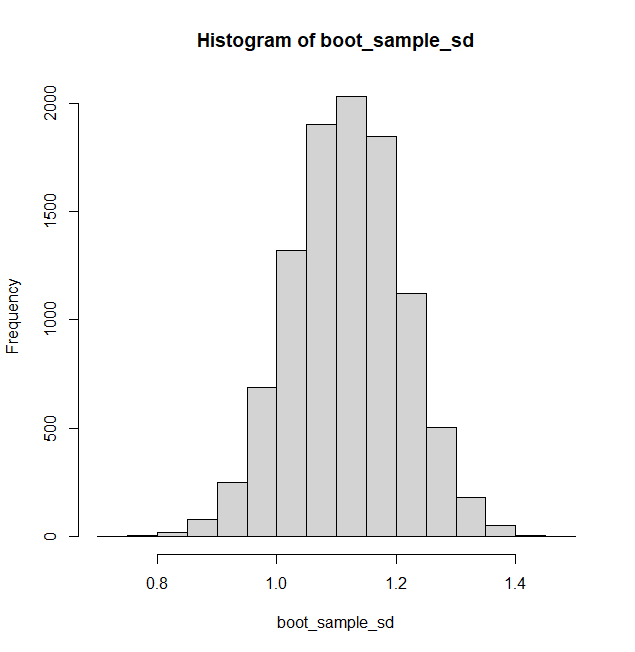
Both confidence intervals contain the true values for the parameter it’s estimating, though the histogram of standard deviations in particular is shifted a little to the right meaning our generated samples perhaps tended to have more variability than the true distribution.