Fraud in the 2020 US Election?!?!

We all know that both during and after the 2020 United States presidential election Donald Trump threw a number accusations of fraud and corruption Joe Biden’s way. One method that has been used in the past to detect fraud in elections is something known as as Benford’s law. In 2009, it was used as evidence of fraud in the Iranian elections and then in 2020 it was found that Benford’s law did not hold for Biden’s votes and therefore many saw this as proof of fraud for Biden’s party… but was it really?

What is Benford’s law?

According to Benford’s law, if you have a large amount of real data you should expect the leading value (first non-zero digit) to be 1 more than any other integer. In fact it should actually be 1 around 30% of the time. The likelihood of a leading digit \(d\) occuring decreases as \(d\) increase.

Here this chart shows the probability of a number having any of the possible leading digits.

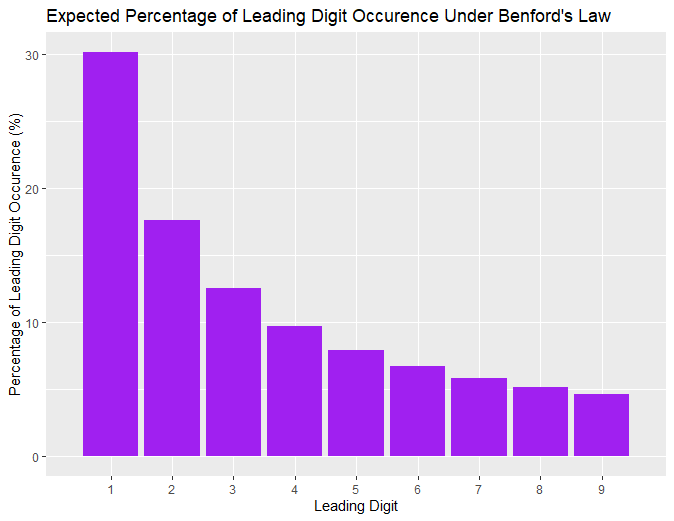
Benford’s law can be used when analysing a large amount of random numerical data to detect various types of fraud. Interestingly, using Benford’s law it was found that the Greek government reported what is very likely fraudulent data to the EU in order to enter the eurozone, however this was only discover later on.

In addition to analyzing the first digit, Benford’s law can also be applied to the second digit and the first and second digits together.

Why is Benford’s law true?

A simple way to think about why Benford’s law holds is to think about it in terms of increasing earnings. If you’re earning £1000 and want to increase this to £2000, that is a 100% increase so you’ll have a leading digit of 1 for a while. However if you are earning an amount of money with a larger leading digit such as £9000 then to get to £10,000 it is just a 11.1% increase so you’ll be able to increase that a lot quicker. This is repeated at the various orders of magnitude (i.e the power when a number is written in standard form, this is often just the number of digits) and leads to having leading values for the proportions expected under Benford’s law.

Benford’s law only holds true when the data spans multiple orders of magnitude. For instance, if the data you have is metric height of adults then it does not hold. This seems obvious when you think about how the majority of adults will have height a leading digit of 1 or 2 (eg. between 1m and 2.99m) and most likley no adult human will have a height with a leading digit of 3 (height of 30cm or 3m – I checked and according to google these have not occured).

What about the 2020 US election?

When trying to prove fraud there were multiple voting districts which were identified such as Chicago and Milwaukee. In Chicago votes were recorded for 50 wards which are split up into smaller areas known as precincts (there are 2069 precincts in total though 15 of these had no votes so were excluded). The leading digit of the number of votes per candidate was recorded for each precinct and then you can plot the frequency for each of the possible leading digits compared to the frequency you would expect under Benford’s law. Here are graphs of these for Biden and Trump.

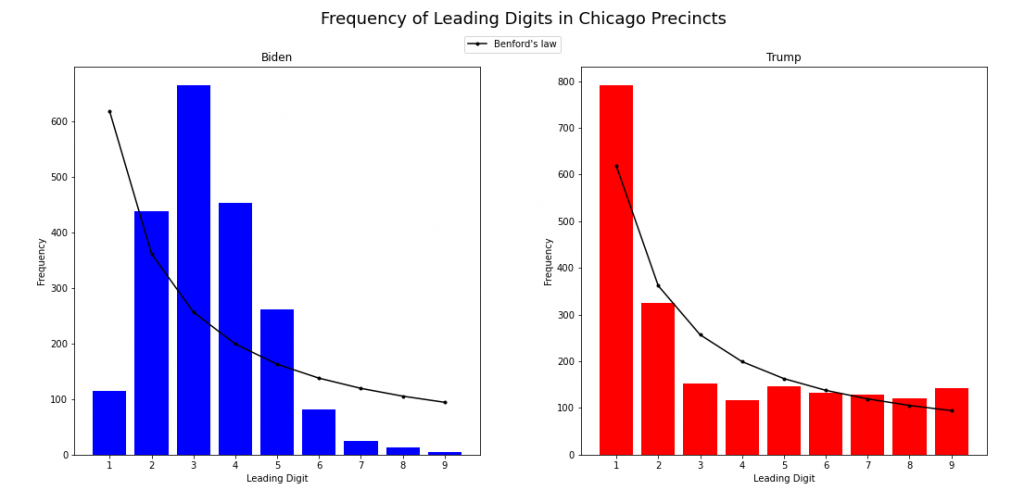
You can see the number of votes Trump recieved in each precinct follows Benford’s law relatively closely. For Biden, however, this is definitely not true which lead many to speculate that this was proof of fraud within the election.

With a deeper look into the data it’s easy to see that there is definitely not a range of magnitudes. The maximum and minimum number of votes in each precinct was 39 and 1418 respectively and the majority of the precincts had vote counts that were a 3 digit number. Therefore you would not expect Bedford’s law to hold and can draw absolutely no conclusions from the fact it does not for Biden.

There continues to be a lot of debate as to whether using Benford’s law to detect fraud in election results is correct though, while in the US 2020 election it was misused, the 2009 Iranian election findings have not been contested. It seems logical that Benford’s law being used to indicate when data isn’t appearing as one would expect can be useful, however this situation proves as a reminder to be cautious when making assumptions. It may also be that in other scenarios, a devation from Benford’s law shows interesting patterns in behaviour rather than outright fraud.

---

References

Wikipedia, Benford’s law, Benford’s law – Wikipedia

Chicago data – Board of Election Commissioners for the City of Chicago (chicagoelections.gov)