A Bayesian Approach To Finding Lost Objects

Ever wondered how they find lost objects in the sea? For example, when a plane such as Air France Flight 447 here goes missing they must have some approach to search efficiently. While there is a small hope of finding survivors of a plane crash, it very useful to find the black box so they can find the cause of the crash and ensure if possible that it doesn’t happen for the same reason in the future. In cases such as this something known as Bayesian Search Theory is used.

What is Bayesian Search Theory?

Bayesian Search Theory applies Bayesian statistics to a search problem in a more efficient way than just randomly searching all of the possibilities. It allows for an updated view on where you are most likely to find an object as you progress through the search. It has been used to find various lost sea vessels such as the USS Scorpion, to help recover flight recorders in the case of Air France Flight 447 and to attempt to locate the remains of Malaysia Airlines Flight 370.

How is it applied?

1. Formulate as many possible scenarios of what could have happened to the missing object using knowledge such as the last known position and the time it was lost. This will also involve a weighting for which scenarios are more likely.
2. For each scenario, assign a probability to the search space of the lost object being in each possible place.
3. An additional probability is assigned based on the likelihood of finding the object in a possible place, given it actually is there.
4. Combining these probabilities gives the probability of the object actually being found if search takes place in a certain area . Areas with highest probability of finding the object are searched first.
5. As the search progresses, the findings (or more appropriately the lack thereof) are used to update the probability that an object will be found in certain area. This is done using Bayes Theorem.

An example

Let’s pretend I dropped my phone in a small perfectly square lake (I don’t think these exist but it makes the example much simpler). I remember using it last when I was on the boat near the centre of the lake and I am certain I must of dropped it when trying to put it back into my pocket. I did drift towards the left edge of the lake after using my phone but I think it’s more probable that it was dropped towards the centre. I’m keeping it simple here with a single possible scenario.

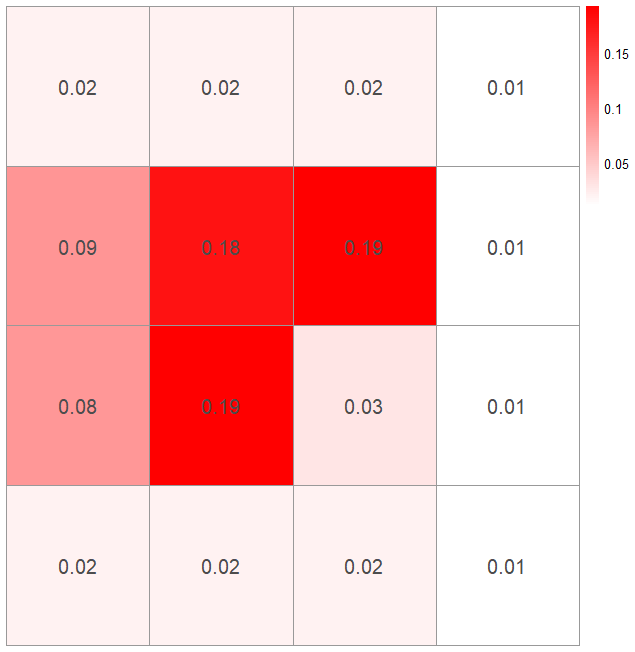
I’ve split the lake up into a 4×4 grid so I’m looking to find which square on the grid to search first. From my assumed scenario of how my phone was lost, I’ve created a probability density map of the space I am searching for the probability my phone has been dropped in a certain square. I’ve also looked into the depth of the lake to create a probability map of how likely I am to actually find my phone in that square given it is there.

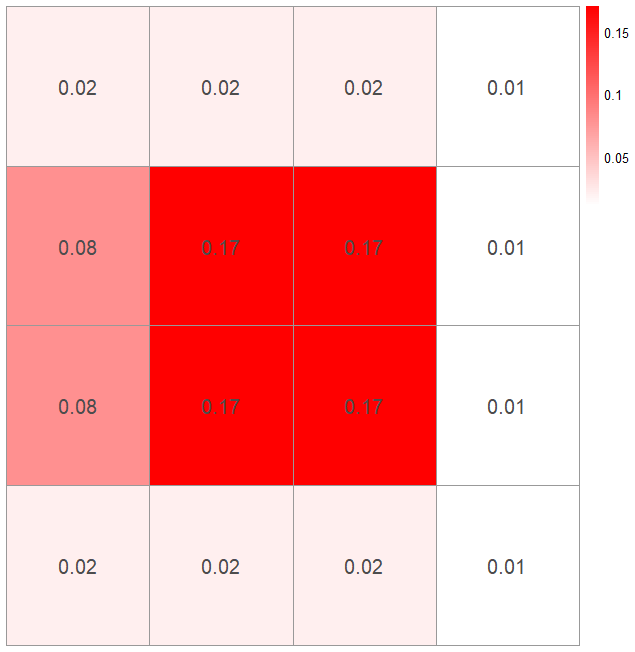
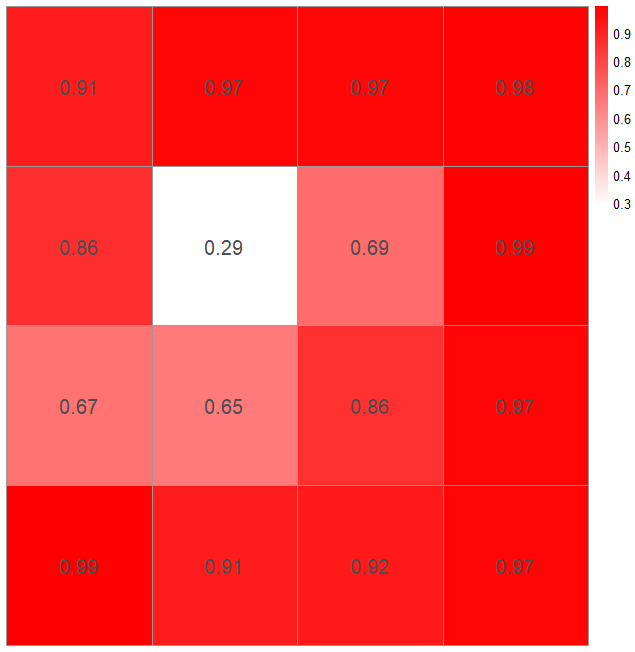
Now I have a map of where to start searching, it looks like the square on the second row up and third column along would be the best option so I’ll search there first.

Unfortunately my phone isn’t there so I’ll use Bayes theorem to update the probability in that square. Applying Bayes theorem and a bit of jiggery pokery with probability identities gives:

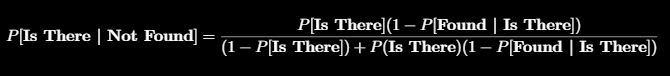
Where P[Is There] and P[Found | Is There] are the probabilities in our two grids originally created. So I can update the probability for that square to be (rounded to 2 decimal places):

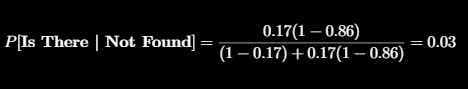
Therefore I update this square to have a probability of 0.03 that my phone is there. I also revise the probabilities for all other squares that my phone is there given it wasn’t found in that first square . For these squares the calculation is

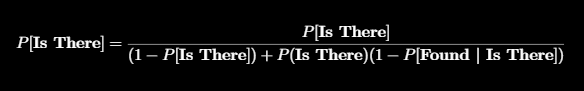
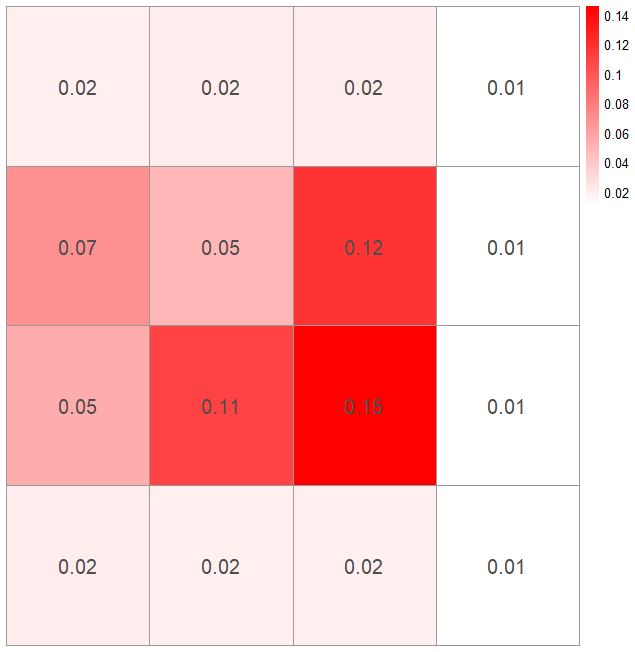
This is then combined with the probability of finding the phone given it is there so I have a revised probability map for the most likely places you will find the actually phone:

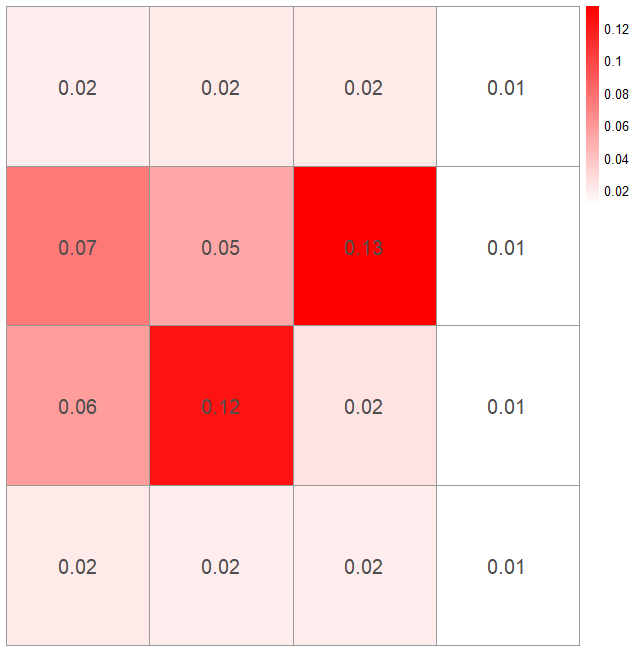
From this I would then move on to search the square with probability of finding the phone of 0.13 and repeat this process until the phone is found.

Practically, always going for the square with the maximum probability may not be the most efficient method because you may have to travel all across the area and it might be more efficient to search areas you are travelling through as you go. After the initial probabilities have been found for the area, a search plan will likely be created for your planned search journey. This may not necessarily have you always searching the areas in descending probability order. However with Bayesian search theory applied you can get a useful indication of where would be wise to search and when to amend your search plan.

---

References: https://en.wikipedia.org/wiki/Bayesian_search_theory