Konigsberg bridge problem and the evolution of Mathematics

Well, In this blog I will discuss one of the problems that led to the development of new branches in mathematics like ‘Graph theory’ and ‘Topology’. Let’s dive into that interesting problem.

What’s the Konigsberg problem?

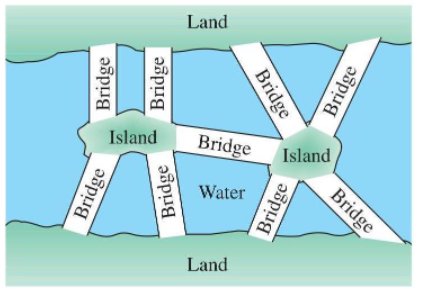
Konigsberg, a city you will find a hard time finding on the world map. However, it is one of the most famous cities in the world of Mathematics due to a particular quirk in its geography. The city of Konigsberg was set on both sides of the Pregel River, and included two large islands, which were connected to each other, or to the two mainland portions of the city, by seven bridges.

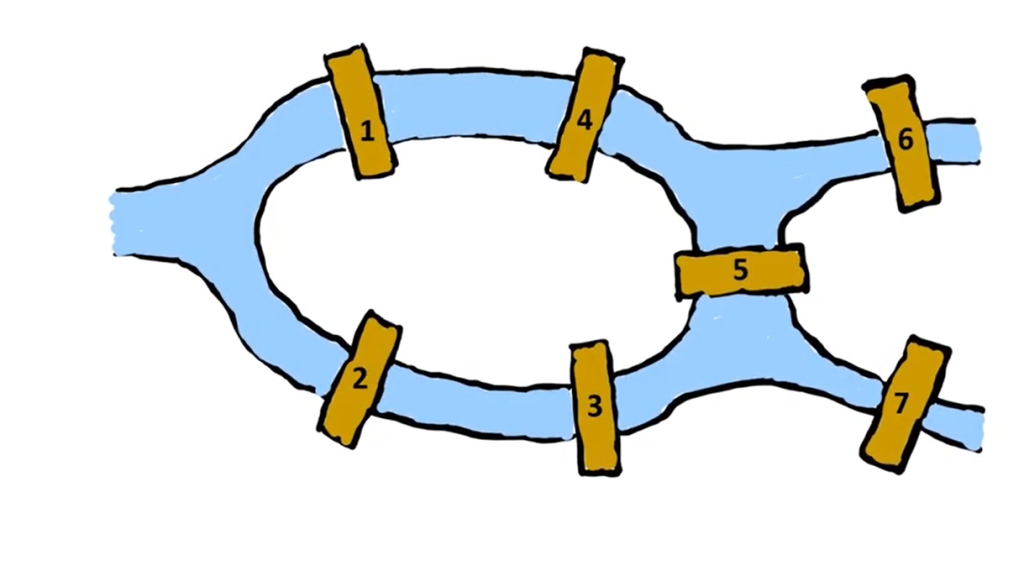
In the 17th century, people were bothered with the question, whether they could walk around all 7 bridges crossing them only once. Let’s try it out!

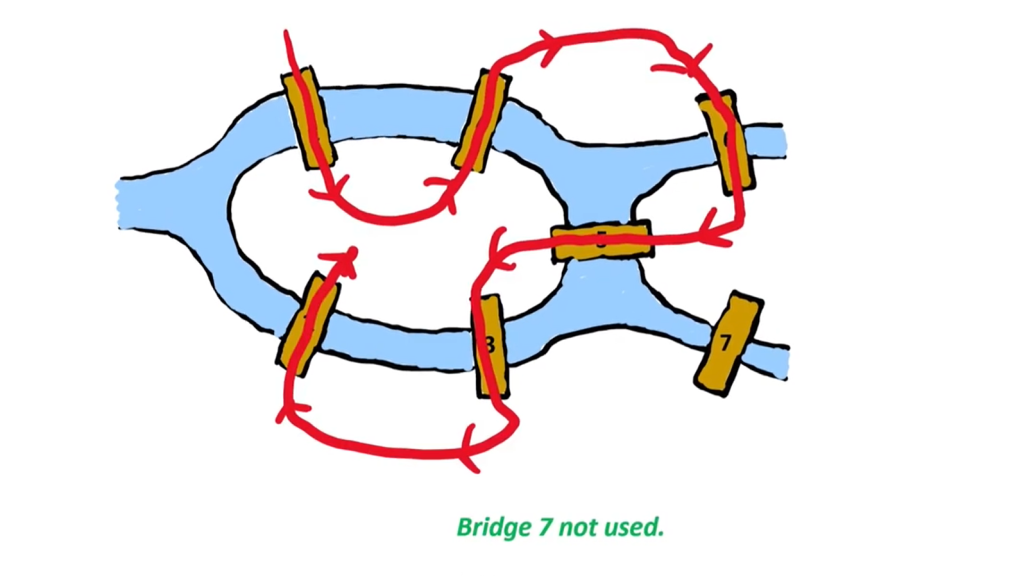
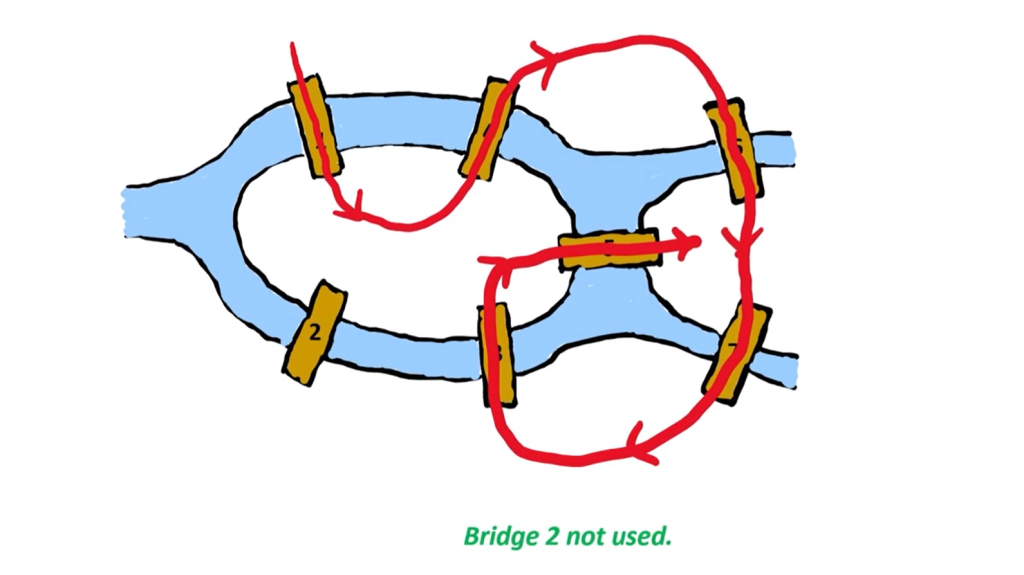
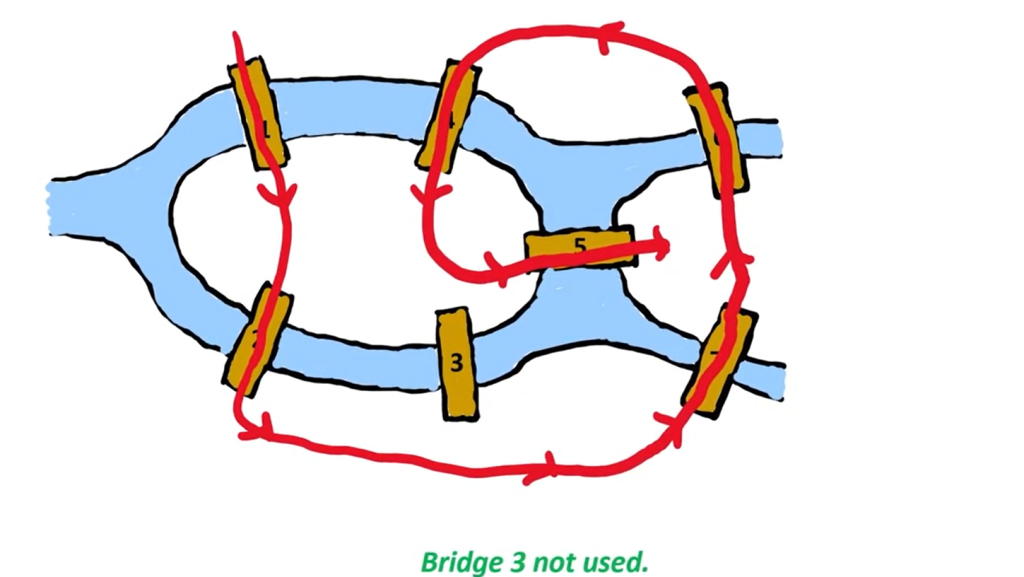
You could very well see other routes in this video and come up with even more routes.

No matter how many ever routes you try you have to give up at some point because Euler answered the question in the negative and proved that there could be no route in Konigsberg that used all seven bridges exactly once and laid the foundation for Graph theory.

How was it proved?

Well, the answer he came up with, did not basically exist then, what he called the ‘Geometry of position’ , now known as the ‘Graph theory’ and which led to the fundamentals of ‘Topology’.

Euler realized during his various trials that the geography or route taken to reach the island or riverbanks does not matter. This insight led to the simplifying of map further. What matters is the 4 landmasses and the relationship between them. We could represent each of the four landmasses here named as A,B,C and D respectively as you could see in the picture below, as a single point, which we now call as Nodes in Graph theory.

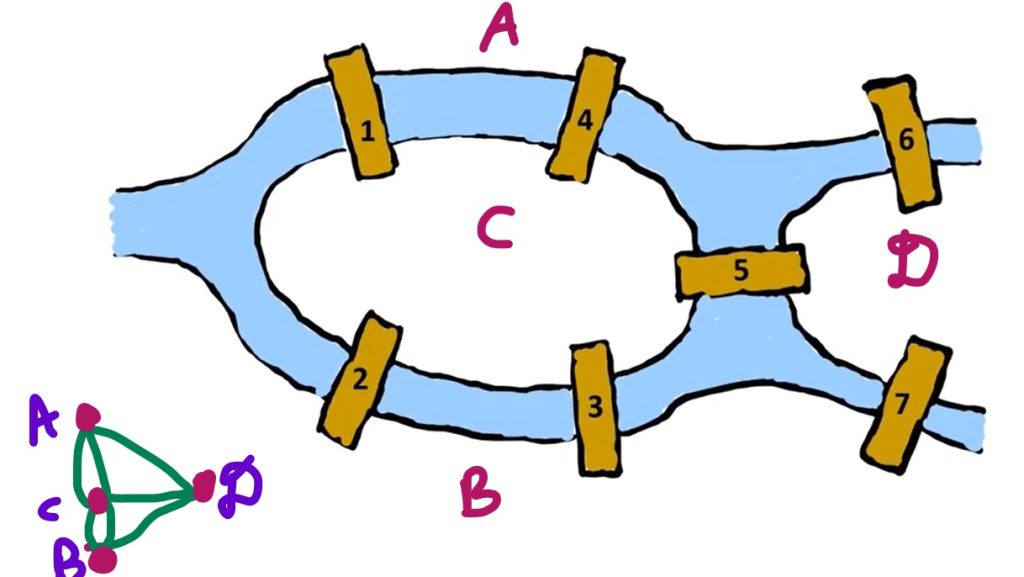
We now have 4 nodes. We draw lines or edges between them to represent the bridges.

Formally, we define a graph G = (N, E) as a pair where,

•  N = {1,2,….N}  is a set of nodes and

• E subset of N x N  is a set of edges between the nodes.

The graph can be used to represent binary relations: (i,j) ϵ E if and only if the entity, i ϵ N and the entity j ϵ N interact with each other. The connectivity of nodes is vital for the structure of the graph. From the simplified graph, as you see in the above picture (Forgive my poor editing skills) with just nodes(Pink dots) and edges(Green lines) we can find the degree of the nodes which forms the basis of this solution. The degree of the node is nothing but the number of edges incident to it. So, in our case, it is the number of bridges that connects to each of the landmass.

According to our challenge, person entering the landmass via one bridge should exit it through another bridge. Technically, edges leading to and from one node should occur in distinct pairs, meaning that the number of edges touching each node must be even. The only possible exceptions would be the locations of the beginning and the end of the walk.

Looking at our graph, we can easily see that all the nodes have odd degree (in yellow in the below figure). Hence, no matter whichever path we choose we will end up crossing a bridge twice.

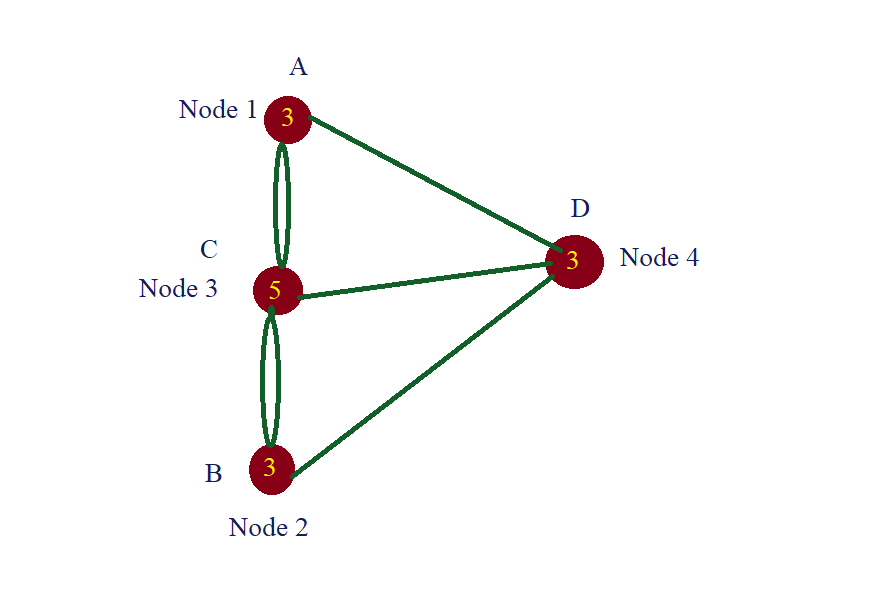
Euler used this as a proof to formulate a general theory that apples to all graphs with two or more nodes. He defined something called Eulerian path that visits each edge only once and is possible only in one of the two scenarios.

1. When there are exactly only two nodes of odd degree
2. When all the nodes are of even degree

In the first scenario, all other nodes would be even and the starting point and ending point are different and should be nodes with odd degree. In the second scenario, starting and ending point would be the same.

Why does it matter?

In the history of mathematics, this is considered to be the first theorem of Graph theory. It basically forms the first proof for Network theory. Network theory in today’s world is a broad area of research. A network is a more general type of data structure that describes relations or interactions between entities. For instance, The Internet network is the physical infrastructure made of internet service providers, servers, routers (entities) and all the physical connections between them. We can never forget the Social networks (Friendships,relationships,work ties, social interactions) in today’s scenario. If time permits, I will discuss more on Social networks in my next blog soon.

Current state of Konigsberg

After the world war II two of its bridges has been destroyed and Eulerian path has been created. However you can’t find Konigsberg now. It is renamed as Kalingrad and is a part of Russia.

I love this particular video explaining this problem in a simple way.

You could well play this game based on this theory. Check if you can draw these line by going over each only once.

https://www.transum.org/Maths/Activity/without/

Further Reading

This lecture notes could quite give you an idea about Eulerian path and this blog could be a great starting point in understanding the world of Graph theory and Networks.