Today’s post is based on a Masterclass given to the STOR-i cohort by Brendan Murphy from University College Dublin.
Clustering
In data science, clustering is the process of grouping objects into groups, or clusters, such that members of the same cluster are more ‘similar’ to each other than they are to members of different clusters.
Many common clustering methods (e.g. k-means or hierarchical clustering) are based off a metric known as the distance or dissimilarity between the points (an example of this distance is simply the straight Euclidean distance between the points). This is then used in a number of different ways to assign points to clusters – for example, in k-means clustering, each point is assigned to the cluster with the closest mean.
While these methods are very popular, they do suffer from drawbacks. Without assuming a model generating these points, it is hard to claim with certainty that future observations will fall into the same clusters. In addition, some of these algorithms can’t properly deal with many frequently repeated observations.
Model-based clustering
Professor Murphy’s Masterclass instead presented a framework for clustering continuous data known as a Gaussian Mixture Model. This is a form of clustering which assumes that the data comes from a particular probability model.
The model is based on 3 general assumptions:
- We know the number of clusters before we start
- Each observation in the data as a certain probability of belonging to each cluster.
- The observations within each cluster follow a normal distribution (with the appropriate dimension)
These assumptions leave us with two problems to solve when fitting the model:
- What are the means and covariances of each of the clusters?
- Which cluster does each observation belong to?
It is clear that these two problems are related. The mean and variance of a cluster will depend on which observations are assigned to it, and the cluster an observation should be assigned to will depend on that clusters mean and variance. Fortunately, there is a way to simulataneous solve both problems using the Expectation-Maximisation (EM) Algorithm. The algorithm works by repeated performing an E-step, which assigns each observation to it’s most likely cluster, and an M-step, which then updates the cluster means and variances based on the assigned observations.
An example – Iris dataset
For a simple example, we will look at clustering different subspecies of iris flowers, based on the length and width of their petals and sepals.

This is a famous data set consisting of 150 observations of 3 different subspecies of iris flowers – Setosa, Versicolor and Virginica (see here for more information on the dataset, including a link to the data itself). I applied the EM algorithm to the data (Professor Murphy kindly left us some code that does this, but the “mclust” package in R also does this). The gif below nicely shows how the algorithm classifies observations and updates the cluster.
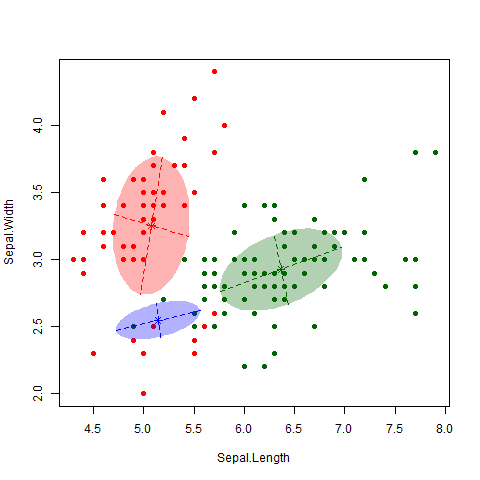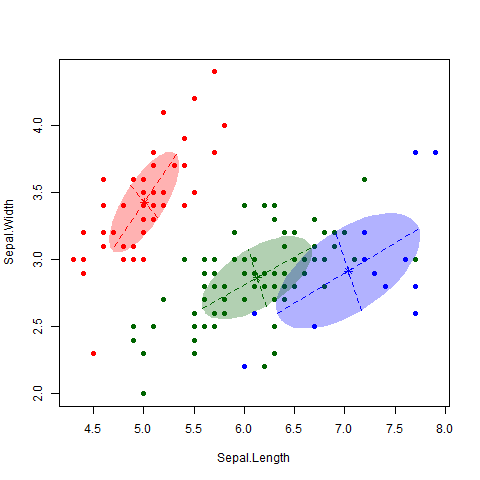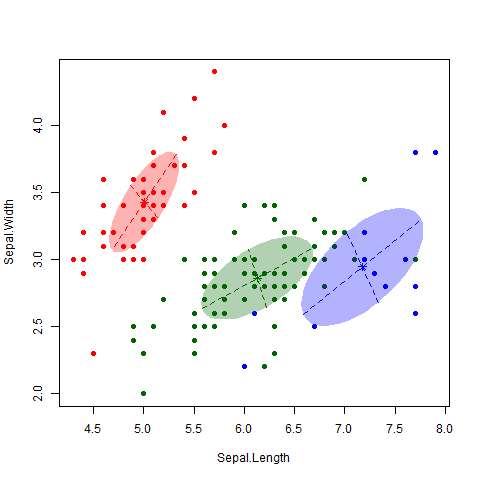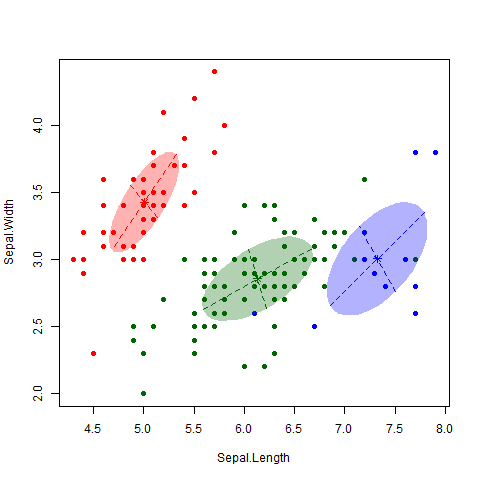
As nice as the above picture looks, the big question is how accurate is the classifier? That is, how well do our clusters match up with the true different subspecies? As shown in the table below, we nailed it on the Setosa. And we did classify all the Versicolor together. Unfortunately, the algorithm couldn’t really distinguish between Versicolor and Virginica. 39 out of 50 Virginica observations were classified as Versicolor. However, it is also worth noting that this dataset is notorious hard to classify, particularly between these two subspecies.
| Cluster 1 (red) | Cluster 2 (blue) | Cluster 3 (green) | |
| Setosa | 50 | 0 | 0 |
| Versicolor | 0 | 0 | 50 |
| Virginica | 0 | 11 | 39 |
Extensions and further work
We’ve barely scratched the surface of Gaussian Mixture Models. Professor Murphy has done extensive work on the different covariance possible covariance structures between clusters (e.g. if you assume all clusters have equal covariance matrices, or simply different scales, or can be whatever you would like). And that’s not even covering classifying with categorical variables, which can be done using Latent Class Analysis. Even taking Gaussian Mixture Models as presented here, you still need to assume the number clusters. While this can be determined using model selection criteria such as BIC, there is still much work to be done in this area.

1 thought on “Model-based clustering”
Comments are closed.