So, the plan for this post was to look at a paper which details a method to make unbiased estimation from Monte Carlo Markov chains. However, in doing that I realised that:
- In order to understand the paper and why it’s important, the reader (i.e. you) need to first understand what a Monte Carlo approximation is… which would be fine, except that;
- The only real way I could fit that into the post would be to embed a YouTube video describing it into the start of the post… which would be fine, except that;
- Pretty much all the YouTube videos on this are really boring.
Therefore, I thought the best thing to do would be go back to basics, and try and give a quick explanation of Monte Carlo Estimation myself. And what better way to give a quick overview is there than another edition of 60 second stats?
So get out the stopwatch, and get ready. The 60 seconds begins…NOW!
What is Monte Carlo Estimation?
Monte Carlo Estimation is a technique used to estimate quantities. It is based around simulating a bunch of random numbers, and then using these to make estimates.
Why is it called “Monte Carlo”?
It is named after the Monte Carlo Casino, in Monaco, which was frequented by the uncle of Stanislaw Ulam, one the methods founders. It is also a reference to the inherent randomness of the method (as all casino games are based on chance).

Ok. So how does it work?
The overall idea is very simple. Say you have a random variable X, and you want to estimate some value related to X (e.g. it’s average). You can then simply simulate a large number of realisations (i.e. copies) of X, and take the average of these. Then (because of the law of large numbers) we know that the average of our copies will be a “good” estimation of X.
Wait, what do you mean by “good”?
What we mean by “good” is that as you take more and more realisations of X to average, the average will get closer and closer to the true value, as shown in the gif below.
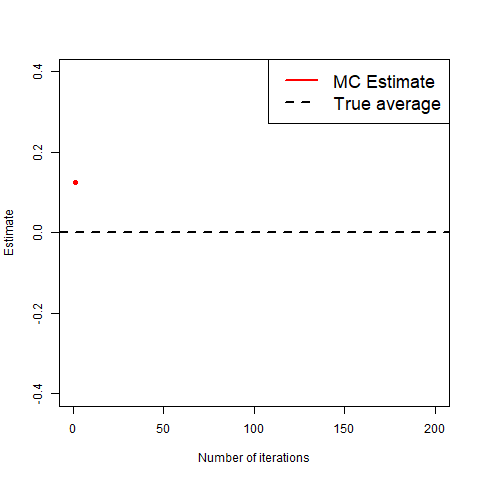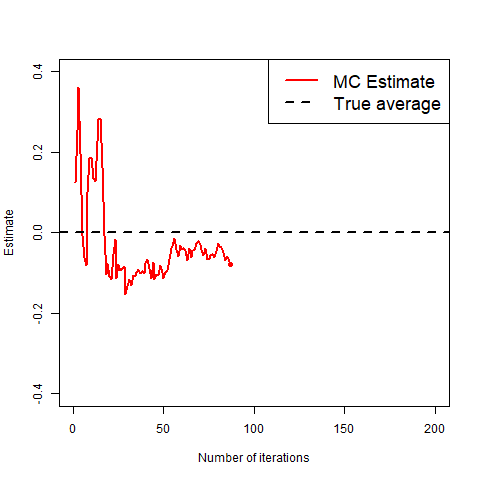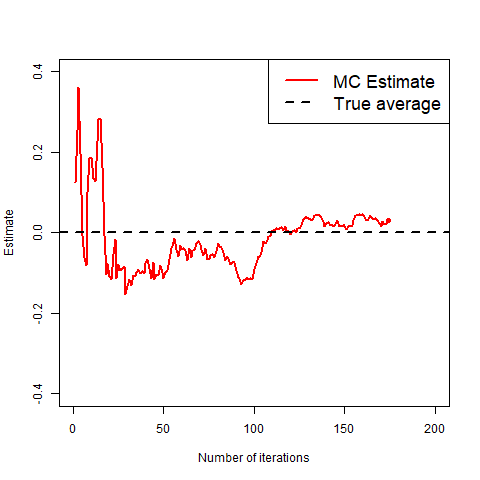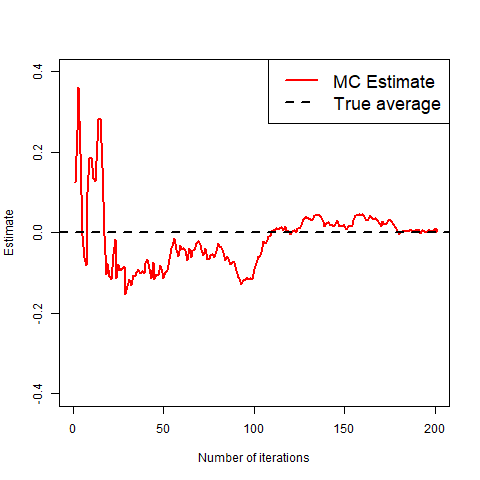
The gif clearly shows that the more copies, the closer to the true value we get.
Alright. So how do I do it myself?
It’s easy! All you need is:
- A method/program/algorithm to simulate copies of your random variable
- Enough computational power/storage to simulate and store many copies of this variable (the more the better)
…and that’s time! Thanks for participating in another edition of 60 second stats. If you want to know more, there are many further aspects to this, such as known results about the variance of your estimates, or what to do if you can’t easily simulate copies of your random variable.