Today’s post will be a choose your own adventure. Follow the prompts and see where you end up!

In today’s adventure, your a humble graduate data analyst trying to streamline queues in an airport for STORi airways, by choosing the right number of check-in desks to open. Due to recent events, the airline is on the brink of bankruptcy, and so this is a very important task. You aren’t very good at analytical calculations, so you decide to simulate the queue to determine the answer.
You ask your boss for some data on arrival numbers are service times. He gives you the arrival times for 50 arrivals all occuring on one day, and the service time for these arrivals.
Right! Time to crack on! You build you simulation model, and get some results for it. You determine the mean waiting time for customers for different numbers of check-in desks. To be safe, you also calculate a 95% confidence interval around these waiting times.
You’re about to take these results to your boss when you have a thought – your dataset on arrivals and service times wasn’t very big. What if it was taken on a slow day? Or the day after the Christmas party, so all the check-in staff were a bit sluggish? What if you can’t trust this data that you made all these decisions on?
If you think “Nah, it’s probably fine” and go to your boss anyway, go to 1. If you think, “Hang on, I better think about this a bit more”, go to 2.
1.
You take your results to your boss, and he seems thrilled. He immediately puts your suggestions into practise. You’re the hero of the office – everyone’s looking up to you, there’s talk of a promotion. But then, a few weeks later you get called back to your boss. You go into his office and the CEO is also there. They’re both furious – somehow the number of complaints from customers about waiting times has gone up. You’re shocked – you ran a simulation! How could this have happened? You bosses pull up the new stats on waiting times. The average times are far longer than you suggested. Don’t worry, you prepared for this. You calmly explain to you boss that the averages may be different, but they should still be in the 95% confidence interval you calculated – they should have known it could be bad. Your boss (who did not seem to appreciate your back-talk) points out that the wait times are even longer than the worst predicted by the confidence interval. You stammer and try to think of an explanation. But it’s too late – the company has already taken a massive hit in revenue, and the boss asks you to clean out your desk…

Thank you for playing this choose your own adventure! If you are upset at being fired, feel free to try again and see if Input Uncertainty could have saved you!
2.
You do some reading and come across “Foundations and methods of stochastic simulation” by Barry Nelson. Flicking through it, you come across “Input Uncertainty”, and you realise you’ve struck gold. The book describes the idea that because the data you’ve used to estimate the inputs to your model is inherently random, this will increase the variability in the outputs, and that you should account for it. But how? The book only gives two suggestions – try and collect more real-world data to reduce input uncertainty, or something called “bootstrapping”
If you go to your boss and ask for more real-world data, go to 3. If you give bootstrapping a go, go to 4.
3.
You go to your boss and ask for more real-world data, explaining your concerns. He tells you (a bit insincerely, in your opinion) that he understands your concerns but time and money are tight, so you’ll have to make do with the data you have.
If you go back and give bootstrapping a go, go to 4.
4.
You start doing bootstrapping. You struggle at first – “resampling? What the hell is that?” you think to yourself. However, the more you try, the more you understand. You start to get the concept – basically, you simply re-draw observations from the data you were given to calculate a new mean each time.
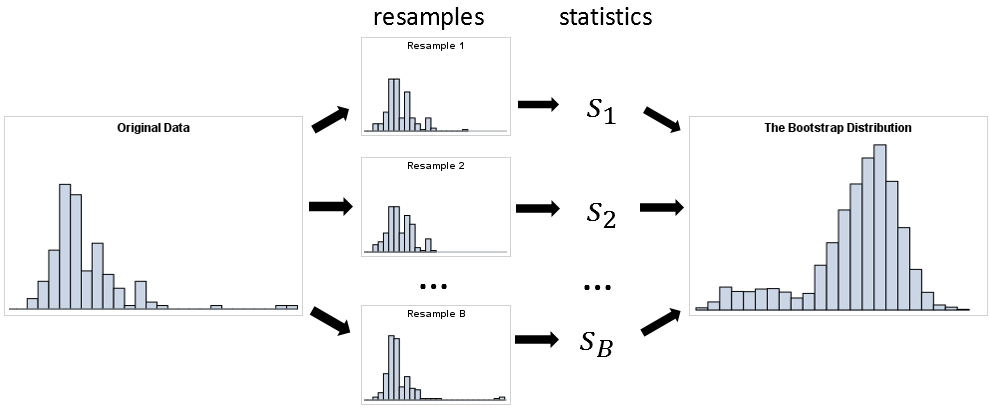
Eventually, by doing this enough, you get a sense of the variability among the means – which, you realise with joy, is your input uncertainty! By using this, you re-calculate the confidence intervals (which are much wider now).
If you take these new confidence intervals to your boss, go to 5. If you think you should try something more sophisticated, go to 6.
5.
You go to your boss with your estimates and your confidence intervals. He reads them, and his face falls. “Good work, but this isn’t great news. We pretty much can’t determine anything from this analysis. The company is looking at some dark times ahead”.
Three months, and a number of layoffs later, you realise that maybe there were some more sophisticated methods you could’ve used. However, it’s now too late. The revenues are falling, and the company is looking at more layoffs.

Congratulations! You didn’t get fired! But that’s about the best you can say about your performance. To see what would’ve happened if you tried something a bit more sophisticated, feel free to try again!
6.
You find a paper giving a very nice review of methods of input uncertainty. It seems that there are a few different methods you can take – and they all have pros and cons. There seem to be three different approaches you could take: bayesian model averaging, meta-model assisted bootstrapping and something called the delta-method.
If you decide to use the Delta-method, go to 7. If you decide to use Meta-Model Assisted Bootstrapping, go to 8. If you decide to use Bayesian Model Averaging, go to 9.
7.
You chose to look into the Delta-method – I dunno, greek letters are cool? – are get to work. You see that the method which uses known mathematical results to decompose output variance into simulation variance and input uncertainty variance. You rapidly decide that this is too mathematical for you, and decide to go back and try one of the other methods.

If you decide to use Meta-Model Assisted Bootstrapping, go to 8. If you decide to use Bayesian Model Averaging, go to 9.
8.
You decide to do Meta-model Assisted Bootstrapping – it’s got the word “Meta” in it, so you think it sounds cool – and get to work. You realise it involves using the results from a bootstrapped sample to try and model a relationship between the inputs and outputs. This model is then used to determine the input uncertainty. This is easy to do since you’ve only got two parameters, and the simulation is reasonably quick. You complete your work and take your results to your manager. He’s astounded – the results are fantastic and show really well how much variability the company should expect around arrival times. Your recommendations are implemented immediately. It works well, and there are no huge unexpected fluctuations. You are hailed as a hero of the office – not bad for your first year out.

Thank you for playing this choose your own adventure! If you want to see what would have happened if you ignored Input Uncertainty, feel free to go back and try again!
9.
You decide to do Bayesian Model Averaging – you’ve heard lots of stats people talk about Bayesian stats, so you think it’s a smart idea – and get to work. Bayesian Model Averaging is similar to bootstrapping, but you weight your bootstrap samples by how likely you think they are, based on your prior knowledge of the sample. That is, when re-taking the sub-samples, make it more likely to select a sub-sample which is more likely given your prior information. However, you don’t really seem to have much prior information to weight your samples on. You talk to you manager about this, and he helps you determine some appropriate priors to use. From this you can create some good confidence intervals for your estimates. Your manager is impressed, and they implement your recommendations immediately. It works well, and there are no huge unexpected fluctuations. You are hailed as a hero of the office – not bad for your first year out.

Thank you for playing this choose your own adventure! If you want to see what would have happened if you ignored Input Uncertainty, feel free to go back and try again!
References
Nelson, B. (2013). Foundations and methods of stochastic simulation: a first course. Springer Science & Business Media.