The seven bridges of Königsberg

During the spring term at STOR-i we were given the opportunity to work on two independent projects with the guidance of an academic supervisor. My first research topic was Extreme Value Theory with Emma Eastoe and my second was on Optimal Patrolling with Kevin Glazebrook. I plan to briefly discus both these projects in future blog posts.

To be able to talk about Optimal Patrolling we will need a basic understanding of graph theory. In this context, the word graph does not mean a plot, with two axis and line showing the relationship between two variables. Instead a graph is an way of repressing and visualizing connections. This is best explained by example and so in this post, I will talk the problem which first introduced me to this type of graph.

The Pregel River divides the city of Königsberg into four landmasses as shown below. Seven bridges (shown in black) connect these landmasses. The problem is then to find a route around the city visiting each of the four landmasses by crossing each of these bridges exactly once. No other means of crossing a river is permitted.

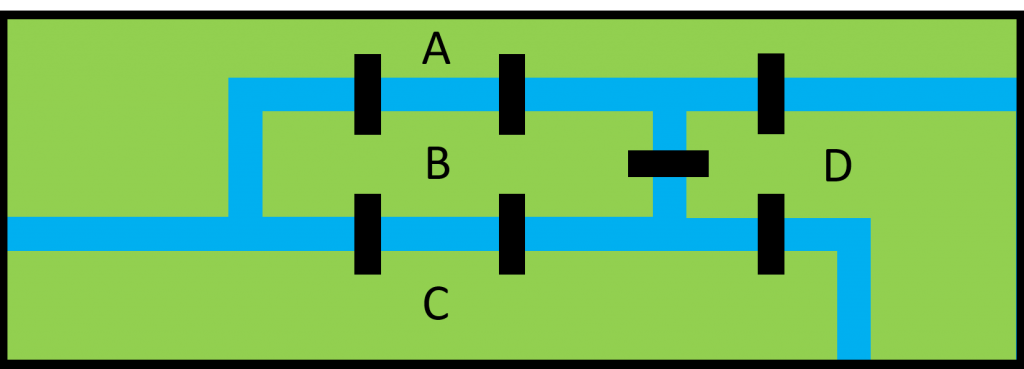
In 1736 a mathematician called Leonard Euler proved that the problem has no solution. A detailed explanation of the proof is given here by the Mathematical Association of America.

The general idea is as follows:

• From inspection we can see that each of the landmasses has an odd number of bridges leading to/from it.
• So it makes sense that if we start at a particular landmass then if we use each bridge connecting to it exactly once then we cannot end our route there.
• Equivalently, for any location that we don’t start we must end our route there.
• Since this implies that we must finish at three of the four landmasses no such route can exist.

We can generalize this problem by thinking of each of the landmasses as a point. The bridges can then be added by drawing a line between the two points associated with the landmasses on either side of the bridge. This is shown for the Königsberg problem below:

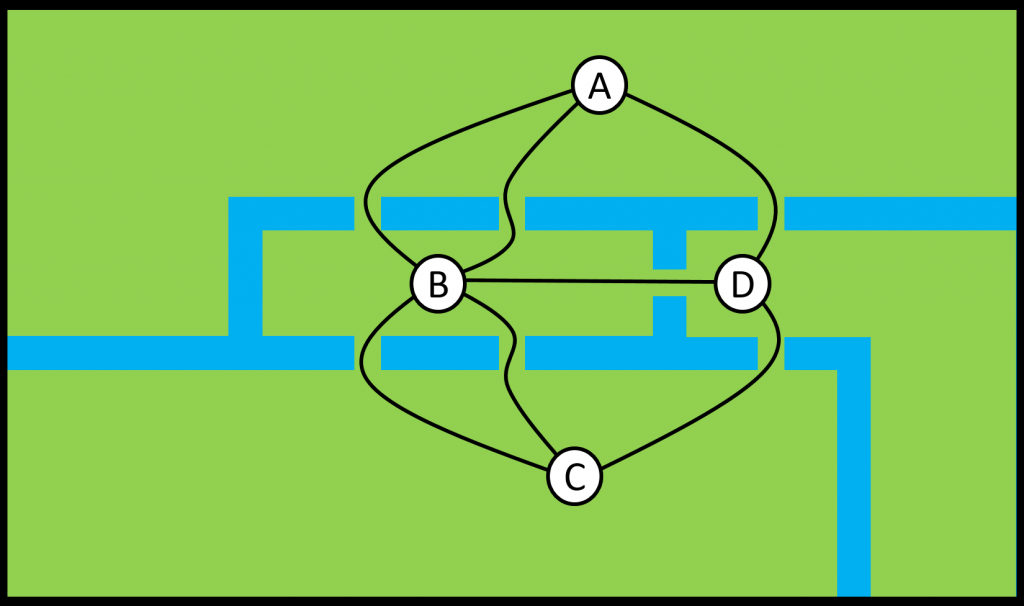
We call this a graph. The points representing the landmasses are called nodes (or vertices) and the lines representing the bridges are called edges (or arcs).

Graphs like this can be used to represent connections in a huge variety of real life situations. For example, we might want to represent the rooms in a museum and the doorways that connect them. We could also consider more abstract connections like friendships between school children. The study of such graphs is called Graph Theory and it was problems like the seven bridges of Königsberg that originally motivated its development. This definition of a graph can be extended to include things like:

• Weighted edges that might represent some maximum capacity of a road connecting two cited
• Directed edges that suggest the connection is only permitted one way. This may be useful if we are using a graph to represent roads which could include a one-way system.
• Hyper-edges that can be used to show a connection between more than two nodes.

In the Optimal Patrolling problem we will use this formulation to represent different areas as nodes and the ways between them as edges.