Game theorists develop strategies for competitive situations where multiple players make decisions, each of which affect the outcome. Each player has some utility function that they are trying to maximise. Usually the best option for a given player is dependent on what the other players choose. Such situations are referred to as games.
In this blog we will discuss a particular type of game called a two-person zero-sum game. This is a two player game where the utility function of one player is exactly the negative of the utility function of the other. It is therefore sufficient to only consider the utility function of one player.
We will consider an example from Alan R. Washbern’s book: Two-Person Zero-Sum Games where each of the players have only two options. Since the players have a finite number of options they can write all possible outcomes in a matrix and so this is called a matrix game.
As promised this example features Sherlock Holmes and his nemesis Professor James Moriarty and is inspired by Sir Arthur Conan Doyle‘s book The Final Solution.

In the book, Holmes boards a train from London to Dover in an attempt to escape from Moriarty. As the train pulls away from the station the pair see each other. Holmes is aware that Moriarty has the necessary resources to overtake the train and be waiting for him in Dover. Holmes now has two options: to take the train all the way to Dover or to get off early at the only intermediate station – Canterbury. Moriarty is aware of these options and so must choose to wait for Holmes in either Canterbury of Dover.
If both choose to go to the same place Holmes has no chance of escape. If Holmes chooses Dover while Moriarty chooses Canterbury, Homes can safely escape to mainland Europe. Finally, if Holmes Chooses Canterbury and Moriarty chooses Dover, there is still a 50% chance that Holmes will be captured before he escapes the county. Thus, we have the following matrix M of escape probabilities where the rows represent Holmes’ choice and the columns represent Moriarty’s choice.
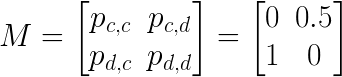
Sherlock wants to maximise his chance of escape so what is his optimal strategy?
There are two ‘pure strategies’ available: to go to Canterbury or to go to Dover. Alternatively, Holmes can create a ‘mixed strategy’ by going to Canterbury with probability p and Dover otherwise. We can recover the two pure strategies by letting p=0 or p=1.
Assume Moriarty chooses to go to Canterbury with probability q then the probability of escape is given by (p + 2q – 3pq)/2. We can see that if Moriarty chooses q=1/3 then this probability is 1/3 regardless of the choice of p. Additionally, if Holmes chooses p=2/3 then he can also ensure the escape probability is 1/3 regardless of the choice of q. If Holmes/Moriarty then changes their strategy, their chances of escape/capture will decrease.
We see that the highest guaranteed utility for one player corresponds exactly to the lowest guaranteed utility for the other. The von Neumann’s Theorem which Washburn goes on to prove in his book (linked above) tells us that this will always be true when both players have an optimal policy.

1 thought on “Game Theory feat. Sherlock Holmes”
Comments are closed.