The last time I travelled, I saw a little old lady in the airport with her crossword puzzle book. My grandmother travels with her word search book. Me? In my old age, I will travel with a Sudoku book. Before I hit old age, I will take advantage of the opportunity to combine my studies with my favourite game. As it turns out, heuristic algorithms are pretty popular for solving, creating and rating Sudoku puzzles. In this post, we will look at how a metaheuristic, general variable neighbourhood search, has been used to solve Sudoku puzzle instances.
- What is Sudoku?
- What are metaheuristics?
- General Variable Neighbourhood Search
- Solving Sudoku
1. What is Sudoku?
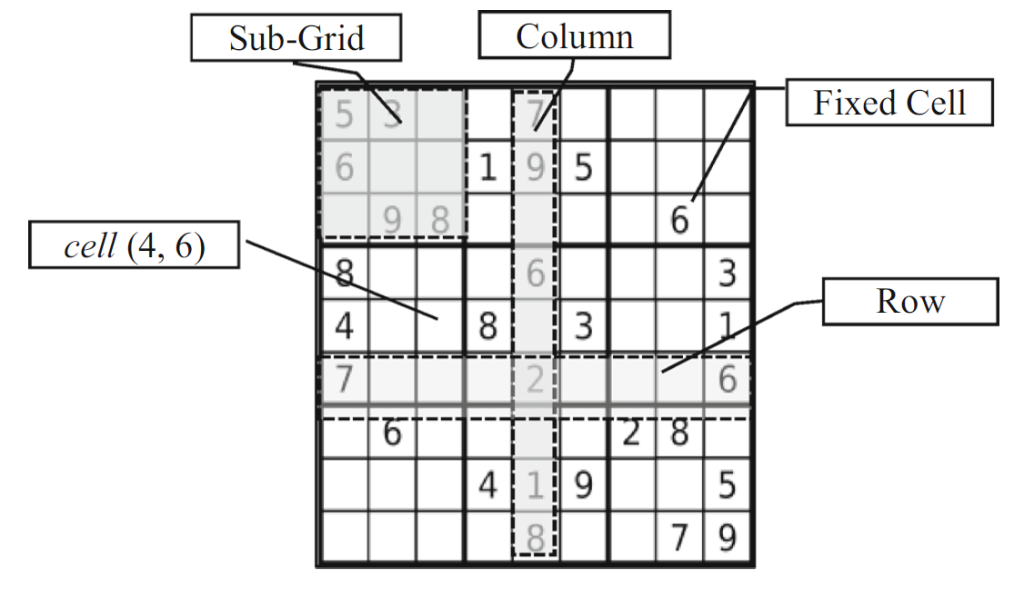
Sudoku is Japanese puzzle which consists of an n2 × n2 grid divided into n2 sub-grids each of size n × n. The word Sudoku is a combination of two Japanese words, Su (Number) and Duko (Single) and loosely translates to “solitary number”. n is the order of the puzzle, with n=3 being the most popular.
The objective of Sudoku is to fill each cell in a way that every row, column and sub-square contains each integer between 1 and n2 inclusive
exactly once.
Sudoku is an example of a combinatorial optimisation (CO) problem, which is a class of problems whose solution is in a finite or countably infinite set. Constructing or completing a Sudoku puzzle from a partially filled grid are both NP-complete problems. This means that there is no deterministic algorithm which can solve all possible Sudoku problem instances in polynomial time. The solution space for an empty 9 × 9 Sudoku grid contains approximately 6.7 × 1021 possible combinations. However, the pre-filled cells serve as constraints and reduce the number of possible combinations.
2. What are metaheuristics?
When it comes to solving optimisation problems, there are 2 main types of approaches: exact methods and approximate methods. Exact methods are guaranteed to find an
optimal solution for every finite problem instance of an CO problem.
Approximate methods such as heuristic algorithms can be used when there is no known exact method that can be used to solve the problem or when the known exact methods are too computationally expensive to be used practically. In the context of optimisation problems, a heuristic is a well-defined intelligent procedure – based on intuition, problem context and structure – designed to find an approximate solution to the problem. Unlike exact methods, the solutions found may not be optimal, but are some type of “acceptable”. The effectiveness of a heuristic depends on the quality of the approximations that it produces.
The performance of heuristics can be improved using metaheuristics, which are high-level,
problem-independent strategies used to develop heuristic optimisation algorithms. They are designed to approximately solve a wide range of problems without needing to fundamentally change.
3. General Variable Neighbourhood Search
Variable neighbourhood search (VNS) algorithms, which were originally proposed by Mladenović and Hansen (1997), are single-solution based metaheuristics. They successively explore a set of predefined neighbourhoods which are typically increasingly distant from the current candidate solution.
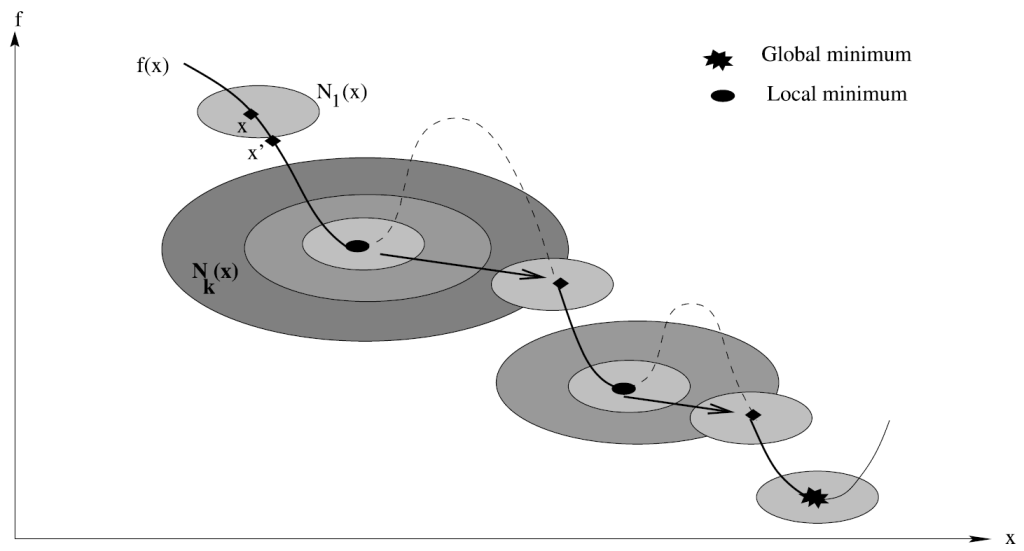
VNS’ main cycle is composed of three phases: shaking, local search and move.
In the shake phase, a random solution s′ is selected from the kth neighbourhood of the current solution s. This s′ is then used as the initial solution for the local search algorithm being used which produces a new candidate solution s′′. In the move phase, if s′′ is better than the current solution s, then it replaces s and the cycle is restarted with this new solution; otherwise, the cycle is restarted with the same solution but a different neighbourhood.

Variable Neighbourhood Descent (VND) is a deterministic variant of the VNS algorithm. The VNS main cycle uses a best improvement method, choosing s′′ as the local optimum in neighbourhood Nk.
The General Variable Neighbourhood Search (GVNS) uses the VND as the local search procedure (line 7 of the algorithm).
4. Solving Sudoku with GVNS
We will now look at the different elements from the algorithm above and how Sevkli and Hamza (2019) used this metaheuristic to solve 9 × 9 Sudoku puzzles.
Solution representation: each sub-grid is numbered from 1 to 9, and each cell in a sub-grid is numbered from 1 to 9. So xij denotes the jth cell in sub-grid i (see grid above for example of labelled cell).
Solution Initialisation: To initialise the solution, for each cell, a random number is selected
from a list of numbers that include all the numbers that could be assigned to the cell without violating any of the constraints with respect to the fixed cells. This is done in such a way that the sub-grid rule is satisfied. To reduce the solution space, they fixed the
cells that only have one possible value and repeated that until there were no more such cells.
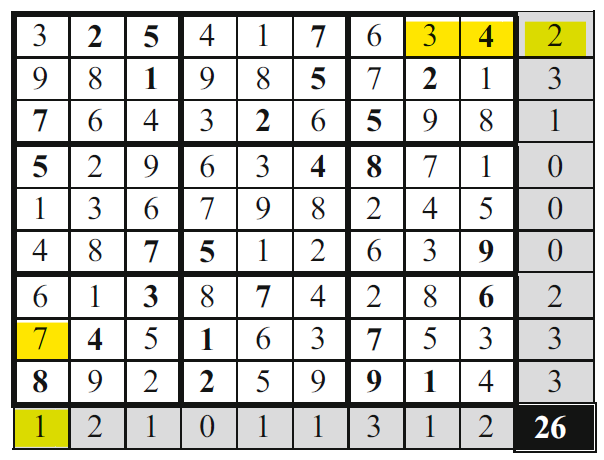
Cost function f(s): evaluates the violation of the row and column constraints and counts how many values are repeated in each row and in each column (illustrated in figure below). The goal is to minimise the cost function. The optimal solution will have f(s)=0.
Neighbourhood structures
Only one neighbourhood structure, Invert, is defined for the shake phase. In this structure two cells in the sub-grid are selected and the order of the sub-sequence of cells between them is reversed.
There are 3 neighbourhood structures defined which are used in the VND local search:
- Insert – the value of a chosen cell in a sub-grid is inserted in front of another chosen cell.
- Swap – the values of 2 unfixed cells in the same sub-grid are exchanged.
- A Centered Point Oriented Exchange – a cell between the second and sixth cell in a sub-grid is selected as the center point to find exchange pairs. Values for pair of cells, each equidistant from the center, are swapped until at least one cell in the pair is fixed.
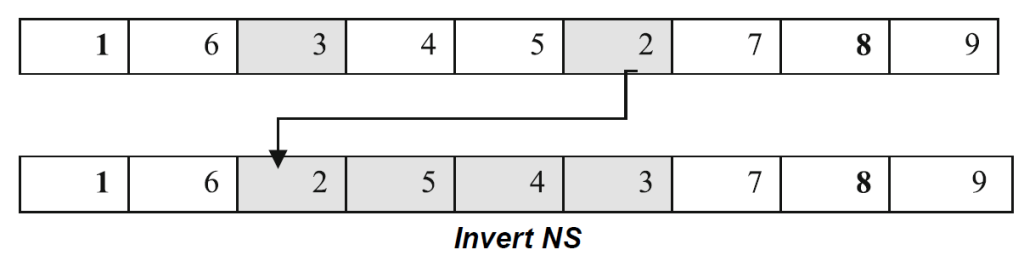
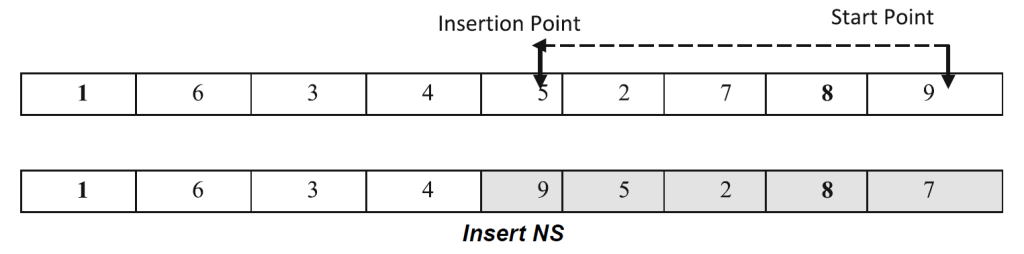
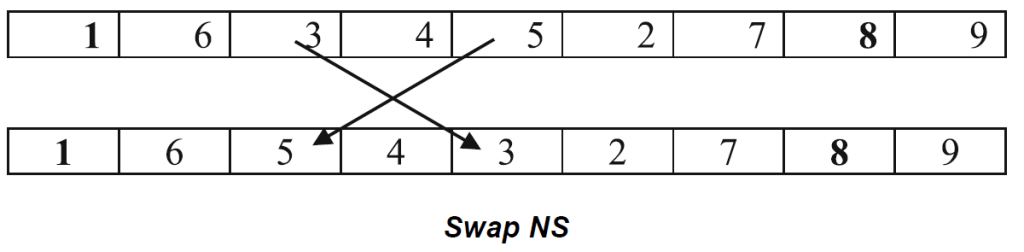
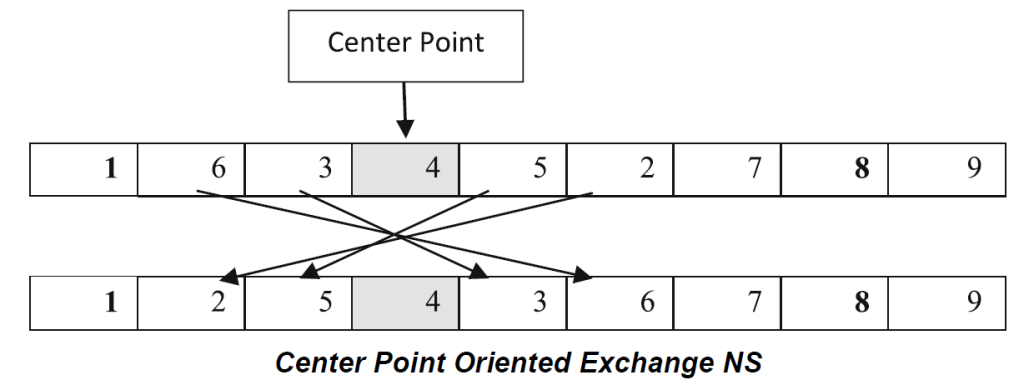
Each of these structures apply to a single sub-grid, and in the local search, the neighbourhoods of each of the sub-grids are explored. Within the VND local search, a deep local search algorithm is used. This uses the best improvement strategy which exploits the whole current neighbourhood structure search area to find the best neighbourhood solution.