Imagine you love karate. You love the principles of the martial arts, you love the physical activity, and well… you love fighting. So you deal with your violent desires in a responsible way – you join your university’s Karate Club. Everything is going great, until there is some conflict over the price of lessons between the club president and the part-time karate instructor. Before you know it, the whole club is divided on the matter and it has become a conflict of ideology rather than just fees. Ultimately, the club leaders fire the instructor, and all of his supporters leave with him and form their own karate club. This is obviously not the type of fighting you had in mind when you joined.
This exact situation was studied by Wayne Zachary, an anthropologist. This and many other situations can be represented as networks to describe the social, physical and other structures where interactions between pairs of units are observed. These include social networks, biological structures, and collections of websites, documents and words.
Stochastic block models (SBMs) are a class of random graph models which are widely
studied and popular for statistical analysis of networks. These networks are modelled to discover and understand their underlying structure, which can be used to group similar elements or simulate how the network could grow. The goal is to infer unknown characteristics of the elements in the network from the observed measurements on pairwise properties.
In this blog, we discuss SBMs using the Karate club example.
- Stochastic Block Models
- Extensions of the model
- Degree-corrected SBMs
- Multi-membership SBMs
- Assortative SBMs
1. Stochastic Block Models (SBMs)
Consider an SBM for the karate club. There are n members, each representing a node in the graph. The members can be divided into K mutually exclusive groups, (B_1 \cdots B_K) . These groups are unknown. What is known about this club are all the relationships between its members, which can be represented in the adjacency matrix \mathbf{Y} . This is an n \times n matrix for the graph where for a pair of nodes (p,q), \, \mathbf{Y}_{pq} is 1 if there is an edge (connection) between the nodes (members) p and q and 0 otherwise.
The SBM is defined by the stochastic block matrix, \mathbf{C}, a K \times K matrix for the graph where \mathbf{C}_{ij} \in [0,1] is the probability that there is an edge from a node in B_i to a node in B_j. A key feature of SBMs is stochastic equivalence. This means that two persons in the same group have the same probability distribution of being connected to other persons, both those within and outside the group. It then follows that for node p \in B_i and node q \in B_j,
\mathbf{Y}_{pq} \sim \text{Bernoulli}(\mathbf{C}_{ij}).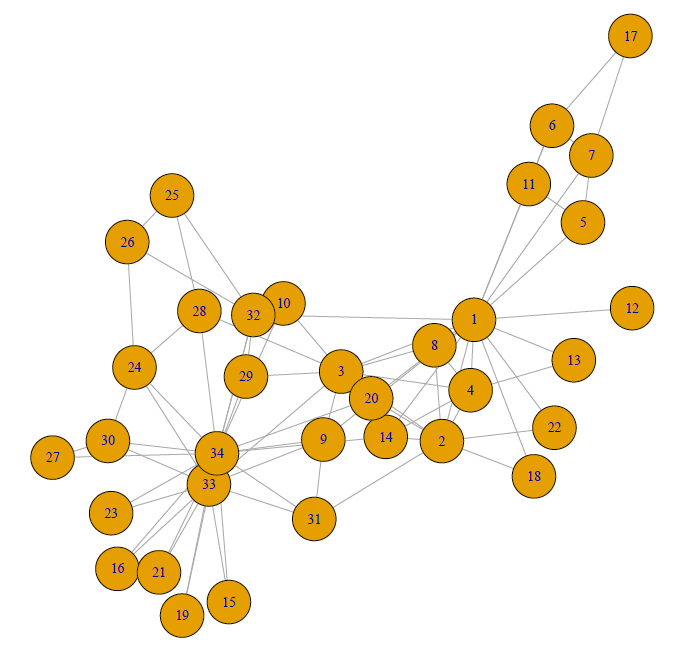
2. Modifications to the SBM
There are several limitations to the simple SBM described above:
- Nodes within a group are expected to all have the same degree.
- Nodes are restricted to belong to only one group.
- The model is not guaranteed to produce assortative groups.
We will now look at a few modifications to the simple SBM that address each of these limitations.
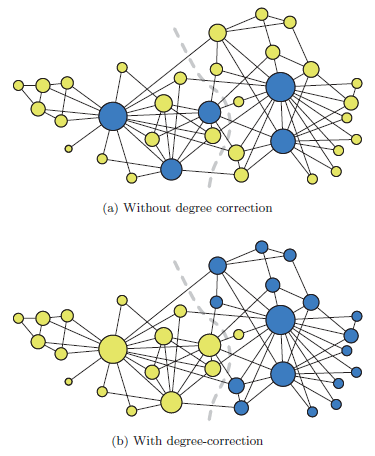
Degree-corrected SBM
In the karate club (and many other networks), it is unlikely that every person in a particular group would have the same number of friends in the group. The degree-corrected SBM extends the simple SBM to account for this possibility of different node degrees.
In an undirected graph, the degree of node p is the number of edges between p and another node. Consider the network as an undirected multi-graph. The stochastic block matrix \mathbf{C} is redefined such that \mathbf{C}_{ij} \in [0,1] is the expected number of edges between nodes in B_i and B_j.
Also included in the model is an n-vector \phi where for each node \phi_p which controls the expected degrees of node p. \phi_p is the probability that an edge connected to the group containing
p is connected to p itself. It then follows that for node p \in B_i and node q \in B_j,
Mixed-membership SBMs
In the Karate club example, the 2nd issue is not all that major relevant (although it definitely could have been possible to be part of both clubs after the split), but it’s clear how for other networks, this can be a major limitation. Further, the strength of their affiliation with each group can be different. The mixed-membership SBM (MMSBM) extends the simple SBM to accommodate these multi-faceted relationships using a mixed-membership approach.
In addition to the variables in the simple SBM, there is also an n \times K matrix of membership probabilities \Theta where each element \Theta_{pi} represents the probability that node p \in B_i. Each row is not restricted to have only 1 non-zero element, so each node can simultaneously belong to multiple groups.
Assortative SBMs
Another consideration is if we want to model a network with a particular goal of grouping
similar elements. For the karate club, there are probably members who are more casual about the situation (they’re just there to fight and go home, not to make friends), and so only have a couple of friends in the club. The simple SBM may conclude that all such persons belong to the same group even if there are hardly any connections in the group because they each have a comparatively small but similar number of friends. This is because the SBM is not designed to prioritize community detection. However, work has been done to extend the model to improve its usefulness in clustering tasks.
Community detection or assortativeness is the property of nodes being partitioned into blocks in such a way that the edge density is high within a group and low between groups. The assortative mixed-membership stochastic block model (a-MMSB) is a special case of the MMSBM we looked at in the previous section. The model includes a parameter
for “community strength”, \beta_i∈ \in (0, 1) for each group which represents how closely the nodes in the group are linked.
Learn More
- A really good review of stochastic block models

Nice post. I learn something new and challenging on blogs I stumbleupon every day. It will always be exciting to read content from other writers and practice a little something from their sites.