As a hopeful romantic, a believer in the principle of marriage and a lover of dating reality TV, I was immediately intrigued by this problem and solution. So to celebrate Valentine’s Day I thought it would be fitting to look at the stable marriage problem.
1. The Premise
Consider two disjoint sets with the same number of elements (for example a group of n men and a group of n women). A matching is a one-to-one mapping from one set onto the other (a set of n monogamous marriages between the men and women). Each man has an order of preference for the women and each woman an order of preference for the men.
A matching is unstable if there exists a possible pairing of a man and a woman (not currently married) that both prefer each other to their spouses. For example, Johnny is married to Bao but prefers Myrla and Myrla is married to Gil but prefers Johnny (IYKYK). Whereas this would making for entertaining TV, the stable marriage problem is to find a matching that avoids this situation.
2. The Pitch
Firstly, it is always possible to find a stable matching in this situation. One possible way to find a solution is the Gale-Shapley algorithm:
First Round
- Each man proposes to the woman he prefers the most.
- Each woman (if she received any proposals) tentatively accepts her favourite proposal and rejects all the others.
Subsequent Rounds
- Each unengaged man proposes to the next woman he prefers the most who has not yet rejected him, regardless of whether she is currently engaged (scandalous!)
- Each unengaged woman tentatively accepts her favourite proposal and rejects all the others.
- Each engaged woman considers any new proposals and leaves her current partner if she prefers one of the new proposals. She tentatively accepts that better proposal and rejects all the others.
The subsequent rounds are repeated until everyone is engaged.
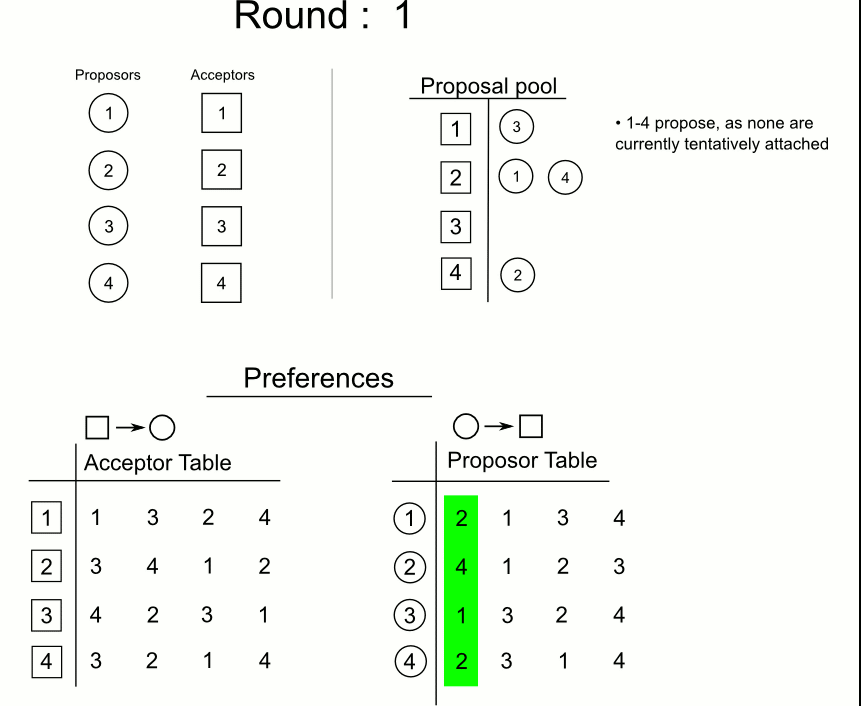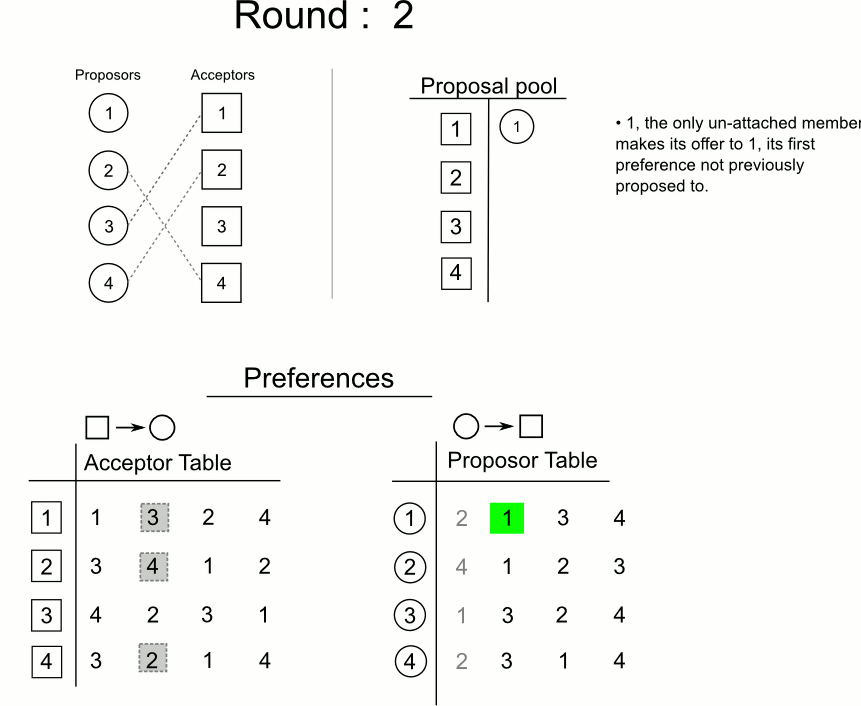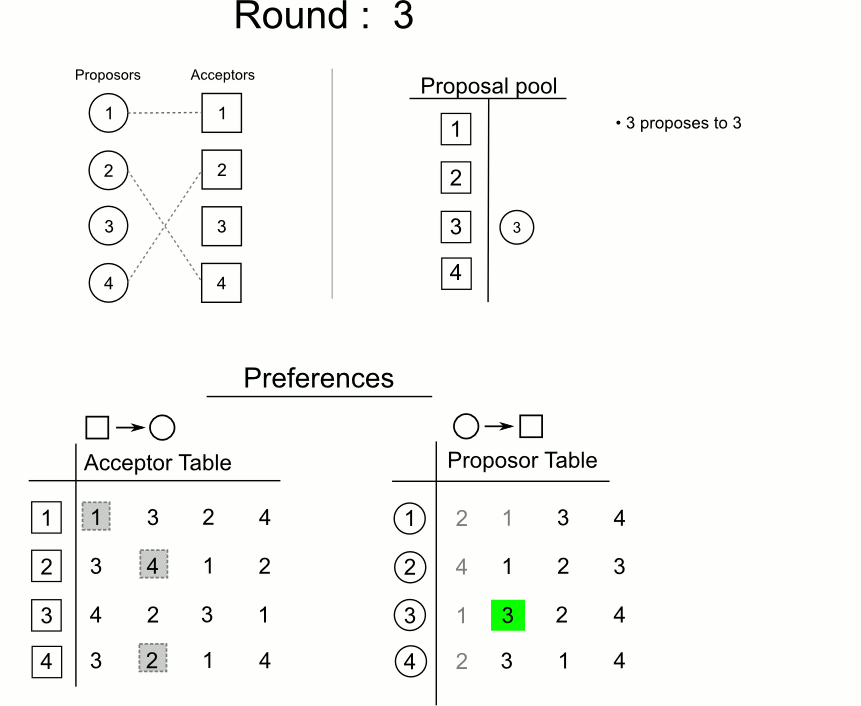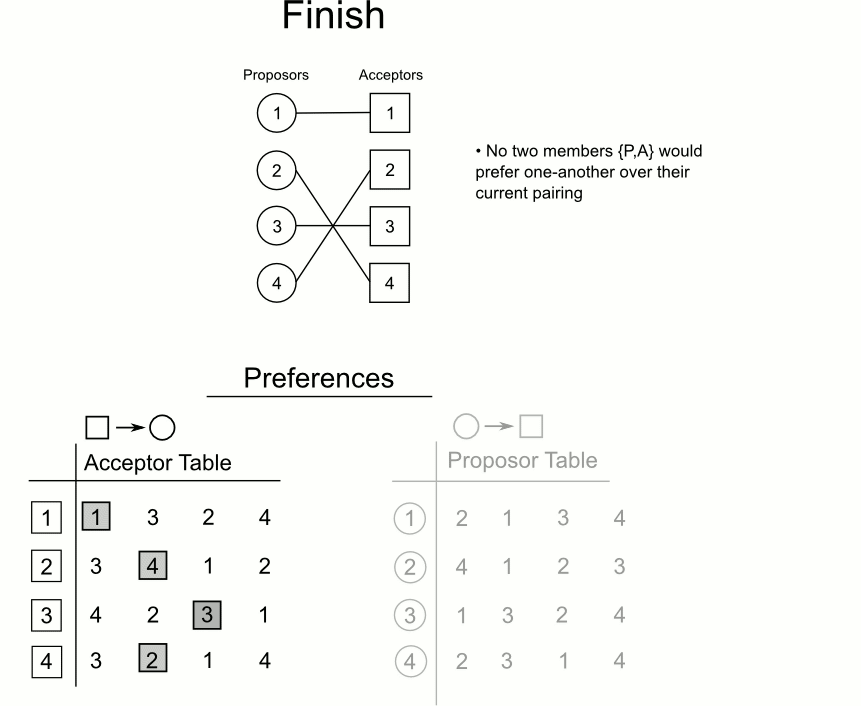
3. A Problem
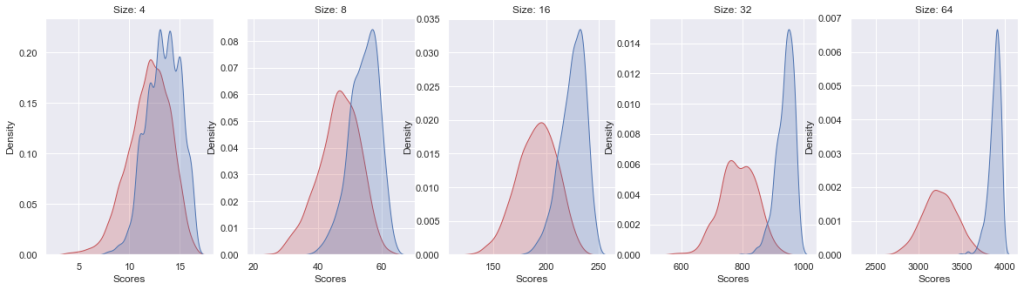
Important for this algorithm is who makes the proposals – if the men propose, the overall outcome is better for them than for the women. If we score each marriage in the stable matching from both the male and female perspectives based on each person’s preferences and take total score for each gender, you can see a clear difference in the distribution of the scores. The difference is more drastic as the set size is increased.
4. In Practice
While I’ve introduced this problem as a pitch for a dramatic (even if biased) match-making show, Shapley and Roth won a Nobel prize for their applications of this problem and someone did his whole PhD thesis extending some of the ideas.
Here are some interesting situations that this algorithm or some variation of it have been used for in practice:
- Placing new doctors at hospitals
- Matching students to high schools
- Matching organs to transplant patients
Learn more
- Gale, D., & Shapley, L. S. (1962). College Admissions and the Stability of Marriage. The American Mathematical Monthly, 69(1), 9–15.

This is such an interesting read! Glad I stumbled on this!