The Monty Hall problem came up briefly in a research talk my MRes cohort attended in January. This apparently paradoxical problem causes debate and confusion, even with mathematicians and is widely misunderstood. Even with a statistical background, it’s sometimes a difficult task to intuitively solve the problem. During the research talk, the speaker asked us (a group of MRes students in a statistical discipline) “which is the better strategy, switch or stay?” and even though, most (if not all) of us would have come across the problem before, none of us were able to give a definite answer with proper reasoning behind it. A few of us gave the correct answer (switch) from memory but the intuition as to why this is the correct solution was still lacking. So, following that talk, I decided to go on a little search for intuition in the hope that the next time this problem comes up, there’s no confusion in my mind.
The Problem
The Monty Hall problem is based on a scenario from the show Let’s Make a Deal where the host (Monty) shows you three doors and tells you that behind two of the doors await hungry goats, while behind the third door sits a brand new car. If you choose correctly, you go home with a brand new car, and otherwise, you get stuck with a goat. Monty asks you to choose a door. After you make your choice, Monty opens a different door and shows you a goat. Now, with only two doors left, you’re given the chance to switch. What should you do?
For someone who hasn’t seen the problem before, a common response, even among mathematicians, is to say that there is no difference between switching and not switching. Two doors left, each has a probability of 1/2 of having the car, right? This response is understandable as we knew there was a goat behind one of the other two doors anyway so we don’t have any new information, right? Thus, intuitively, it’s easy to see why someone might argue that each remaining door has a 50\% chance. This is incorrect. The correct choice is actually to switch, and with this strategy, the odds of finding the car double! Let me explain why.
Explanation
A common misunderstanding here is that, after you’ve made your initial choice, Monty opens up a door at random. However, what actually happens is: Monty, knowing what’s behind every door, opens up a door to show you a goat. Now, there’s a couple of ways of looking at the problem once you take this into account. First, let’s start by assuming we play this game a large number of times and we now want to choose the best strategy to use throughout all of the games. Clearly, staying with your initial choice will work 1/3 of the time since the probability of the car being behind that door is unaffected by the new information. There’s only two strategies to use so if staying will only work 1/3 of the time, then switching must work 2/3 of the time.
Now, this may seem like weak logic and you may still argue each of the doors left has an equal chance of having the car behind it. But the key here is that Monty knows what’s behind all of the doors!
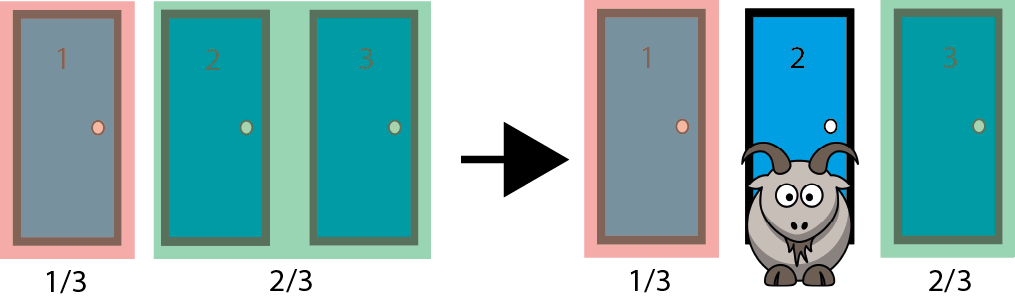
So let’s look at this again. Once you’ve made your initial choice, say door 1, there is a 1/3 chance that the car lies behind door 1 and a 2/3 chance that it lies behind either of the other two doors. Now, Monty opens, for example, door 2 and shows you a goat. At this stage, door 1 still has a 1/3 chance but with door 2 having been opened, door 3 now holds the 2/3 probability of having the car. So, we might say that the probability has now been “concentrated” on the only other door left leaving it with double the probability of having the car! So, clearly, we should always switch as this will allow us to win two thirds of the time.
Larger Scale
To make this a bit clearer, let’s imagine we, instead, have one hundred doors from which to choose:

Suppose you still make the same choice of door 1. Now, there’s a probability of 99/100 that the car lies behind one of the other doors.

Following this, Monty shows you 98 doors with goats behind them. So, what would you do in this scenario? Immediately, this makes more intuitive sense. Since Monty knows which door holds the car and has shown you 98 doors without it, you, of course, should switch to the one door he avoided opening. Following the same process, door 1 which you initially chose has a 1/100 chance of having the car while the one other door that’s left unopened, say door 97, has a 99/100 chance!

Conclusion
The conclusion from this post is simply, ALWAYS SWITCH.
Switching is clearly the better strategy. As demonstrated above, if you played the game a large number of times, the switching strategy would win approximately 67\% of the time whereas sticking with your initial choice would win only 33\% of the time. So, the former strategy doubles your chances of winning a nice new car!
Hopefully, this post has cleared up this debate-inducing problem. Feel free to leave a comment or reach out to me through the contact form here if you’d like to discuss it.
Thanks for reading!