Historical insights into the birth of a crucial subfield of Operational Research.
“It happened because during my first year at Berkeley I arrived late one day at one of Neyman’s classes.”
– George Dantzig, College Mathematics Journal
George B. Dantzig, a first year doctoral student at UC Berkeley, mistook a set of unsolved problems in statistics for a homework question. Scribbling them down and solving them over the next few days, Dantzig had found these problems slightly harder than a normal homework assignment. He threw his solutions onto the desk of his professor; expecting them to get lost within the clutter of Neyman’s office.
“About six weeks later, one Sunday morning about eight o’clock, [my wife] Anne and I were awakened by someone banging on our front door. It was Neyman.” Dantzig recalled in a 1986 interview for the College Mathematics Journal. What the young student had done, initially unbeknownst to him, was solve these statistical problems and had a giddy professor already writing his papers introduction to be sent for publication. From this, Dantzig begun a journey into mathematical stardom.
Eight years after this tale, forever ingrained into the minds of wannabe mathematicians, Dantzig was working as a mathematical advisor for the pentagon. Tasked by his department to computationally speed up logistical issues faced by the US Air Force, he developed techniques stemming from the infant field of Linear Programming to optimise said issues. The method used was to be known as the Simplex method, but where does it come from and who are the significant players in Linear Programming?
Two more key figures
The ideas of Linear Programming in the history of mathematics often starts with Dantzig’s contributions, but its origins can be dated back to a few years earlier during World War II. Namely in the field of economics and with Soviet economist Leonid Kantorovic. In 1939, he developed the first forms of the Linear Programming problem for organising and planning production. Cited as a founder of the field, Kantorovic’s method revolved around finding dual variables and corresponding primal solution, linking how the results from one directly impact the other. The ideas of Primal and Dual simplex are key components of linear programs, however they consist in a slightly adapted form than what Kantorovic designed. They are not explicitly covered in this post, but the eager can venture here to see more on the topic. Kantorovic would later go on to win the Stalin Prize for his work in resource allocation stemming from ideas he developed in the operations research field.

Another important character to this field, amongst many others, was John Von Neumann. He was a proverbial rockstar in the mathematical world, dabbling in a variety of topics from quantum mechanics to game theory to the early days of computer science and most importantly to us, Linear Programming. He contributed an important aspect to this field, Duality Theory, involving the ideas of Primal and Dual Linear Programs recently touched upon. Without explicit knowledge of what this entails, it should be important to understand that this concept is pivotal to expanding and solving more complicated Linear Programs and highlighting a connection between optimisation by maximising or minimising.
Solving Linear Programs
While these aforementioned figures crafted a field in which decisions of optimality can be expressed simply as a set of linear inequalities, a key issue still remains… how do we solve these?
Recall Dantzig’s work with the Pentagon, his eventual solution to conundrums regarding optimal solutions for planning methods didn’t arise as quickly as his infamous Berkeley story (it might be of interest to know links between this story and inspiration for the movie Good Will Hunting is pretty strong). Instead, the acclaimed Simplex Algorithm was the result of an evolution from his PhD work six years prior. Here, Dantzig developed an algorithm that could solve sets of linear inequalities, with the aim of maximising or minimising some objective.
A quick example of what this objective could be is, for example, thinking of a fruit seller, figuring out how to maximise profit, with different fruits having certain purchase restraints, cost requirements, life expectancy etc.. While these problems may not have been at the upmost important to Dantzig at the time, these motivating ideas at least warrant some kind of solution that is optimal. His Simplex Method of 1947 did just that and, at the surprise of Dantzig himself, had an incredible track record for being an effective method.
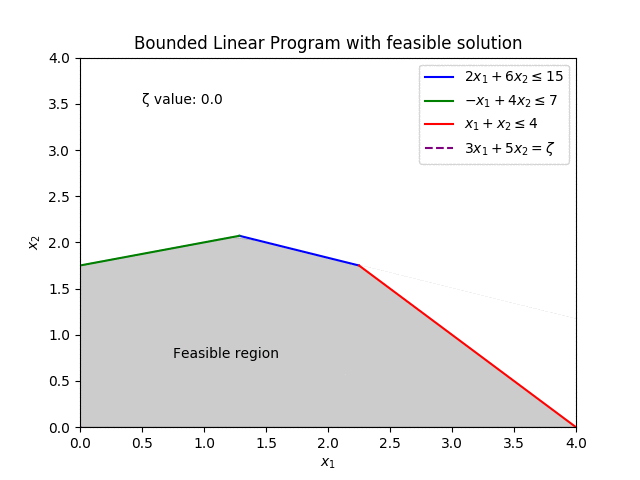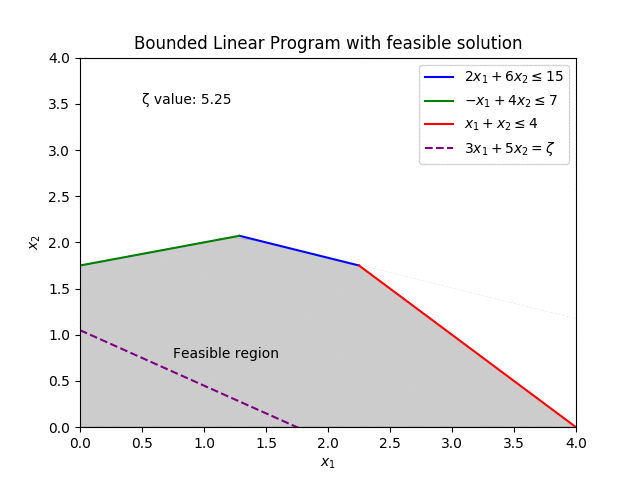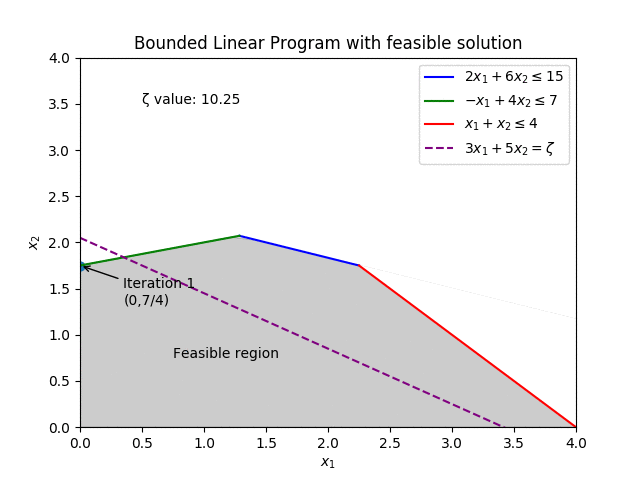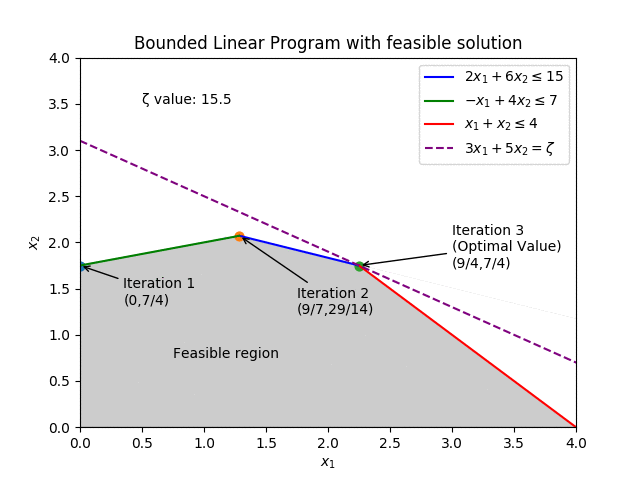
Decades later, where it is commonplace for new methods to come in and improve on the old, finding unique and novel ways to push the boundaries, the Simplex is still regarded as a strong contender for the best method at solving Linear Programs. With industrial solvers still employing the 75 year old method.
This blog covered a purely historical aspect of the method and some further reading can be found in these interviews and overviews of Dantzig:
- https://apps.dtic.mil/sti/pdfs/ADA182708.pdf
- http://www.personal.psu.edu/ecb5/Courses/M475W/WeeklyReadings/Week%2015/An_Interview_with_George_Dantzig.pdf
A more wider history of linear programming, and its wider family of Operational Research can be uncovered in the following compendium of resources:
