Following on from the previous blog post, we now consider the cliffhanging suspense we left off at by answering the question on modelling events where we may change our opinion. With a hearty – but slightly more forced bird analogy – and reference to a less glamourous bird chaos movie, we proceed in true sequel fashion!
Beyond consistent approaches
Now it may have dawned at some point that individuals, both of the human and bird-human monstrosity variety, could change their risk strategies depending on the progression of a situation. Two people that did such a thing were Milton Friedman and Leonard “Jimmy” Savage, formulating the idea that people could have multiple attitudes to risk and formulated a utility function that has both convex and concave periods. They began their argument through posing a question asking why people purchase both insurance (a risk-averse behaviour) and lottery tickets (risk-seeking behaviour), this goes against the consistent rational ideas originally found in VNM Theory. Although it should be stressed, this is simply an extension to VNM Theory and not a replacement to the ideas.
The function they derived presented a model to which it explained why at the extreme levels of wealth (both poor and super rich) risk averse patterns are observed, whereas in the situation when they are moderately wealthy, risk-seeking approaches are made. A short summary of these ideas can be found in this article, it is not necessary to fully understand why they came to the conclusion they did, just perhaps some self justification as to why shifting risk patterns can occur.
The overarching idea of shifting risk attitudes can now be applied to our bird example. Now, assume the bird is looking for a certain quantity of food to survive, except there is a threshold as to which the bird will turn from not having enough food (a scarcity) to having enough food (a surplus) to survive an arbitrary amount of time. Again these are not ravenous birds.

This culminates in a proposal utility function compromising of a piece-wise function (i.e. there are multiple sub-functions applied to different intervals). For when we are risk-seeking and are requiring food for survival, re-using U(x)=x^2 could be a reasonable model for this, whereas when we have enough food and purely here to maintain the quantity, U(x) = log(x) is proposed. We can see this in the below graph.
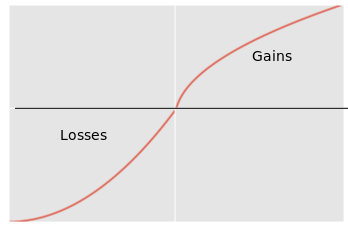
(U(x) = ln(x)).
There are issues with this approach, predominantly that it assumes the bird isn’t as risk-averse as it is risk-seeking. In some sense it might make more sense for this to be the case. In this scenario we could perhaps use something akin to the the logistic function to model this risk attitude.
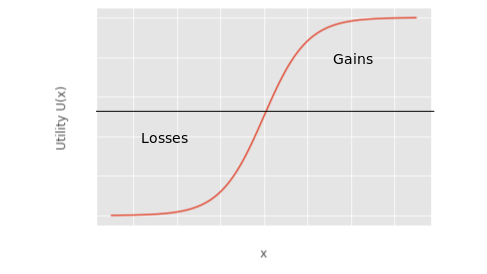
U(x) = (1 + e^{−x})^{−1} .
With this, we have been able to construct a model for rational behaviour for this bird and that it can now go forth and implement these ideas into their food scavenging endeavours.
Conclusions and further reading
In the previous post it was noted that expected utility belonged to a cacophony of approaches, and hopefully as we progressed through these ideas on how we postulate our own rationality and the decisions we make, doubts and questions may have arisen. Namely on the mess that was the bird example, but also on is questioning if this the only way to measure rational thinking and the choices we make under uncertainty.
Prospect Theory provides another school of thought and has a prominent place within the economics field. Introduced by Daniel Kahneman and Amos Tversky in 1979, they rely less on axiomatic predispositions that are assumed under VNM Theory, and instead assumes the decision maker may not have idealistic approaches to rational decision making. Therefore it aims to model what people actually behave like, with this area being more focused in the world of Economics and Psychology. For a view more closely aligned with VNM Theory, Jimmy Savage, referenced earlier with his special utility function, presented more thorough exposition of expected utility with a Bayesian approach of expected utility given by Savage’s representation theorem, contained within his work “The Foundations of Statistics“.

