Optimising with Ants and Ice-cream Cones
26th January 2016
Over the next two weeks, we are having short introductions to ten different research topics that are studied by researchers here at
Lancaster University, both in Statistics and in Operational Research. These topics will vary from Extreme Value Theory to Logistics,
Transportation and Operations. Within each broad topic, three or four different researchers are to give us a one hour lecture showing
a brief overview of some of the topics they work on.
Yesterday, the overall topic was Optimisation. Under that heading, we had three lectures, Search Based Optimisiation and Applications,
Multi-Objective Mathematical Programming Optimisation, and Conic Programming. I wish to talk briefly about each of these.
The first talk was given by Michael Epitropakis and titled Search Based Optimisiation
and Applications. He spoke about his research in Stochastic Search Optimisation Algorithms (SSOA) and Metaheuristics. These are heuristic
approaches to optimisation problems that use some element of randomness in the search for the optimal solution. Many problems that
occur in real life are non-convex, NP hard, high dimensional or have discontinuities. Alternatively, maybe we cannot evaluate the
objective function perfectly, as was discussed in my last post (Optimisation and Error in Simul?ation).
When this is the case, exact methods,
those for which convergence to a true optimal solution is proven, are not practical or will get stuck at a local rather than a
global minimum. Some of the examples that Epitropakis has worked on included optimising the trajectory of a probe between planets and
aircraft scheduling. There are many types of metaheuristcs including evolutionary algorithms such as genetic algorithms that adapt to
the problem as it is running, and population based searches like Ant Colony Algorithms. Whilst I have no doubt as to the effectiveness
of these Metaheuristic approaches, they still lack mathematical proof and this leaves me with reservations about the topic.
The design of a SSOA requires three different parts, representation, a search strategy and a fitness function. The representation is
the requirement that every possible state of the system must be represented. The search strategy gives the rules for how to move around
the space of states. The fitness function is a way of assessing the states and how good they are. One question being researched
is that of automatic design. If a program is given a problem, it should be able to choose what to do and how to
approach it. The advantages of this idea is that is it is more flexible and can get a better fit to a general problem. However, the many
components can make it difficult to assess the performance of a state.
The second talk was on Multi-Objective Mathematical Programming Optimisation and was given by
Matthias Ehrgott. In a normal optimisation problem, one has an
objective function $f(\mathbf{x})$ which one wants to minimise, but what if $f:\mathbb{R}^n\rightarrow\mathbb{R}^p$ and so has a vector
as an output? This requires a new definition of what we mean by minimising a vector. This is done by minimising the different elements
separately. First, let $X$ be the set of feasible solutions and $Y=f(X)$. The best solutions will always be on the border of $Y$, as
otherwise one can always move closer to the origin. However, even some solutions on the border can be improved upon.
The main method we discussed was Weighted Sums. If each of the $p$ objectives has a real valued objective function $f_i(\mathbf{x})$, then
we choose positive real numbers, $\lambda_i\in\mathbb{R}_+$, and create a new objective function
$$\hat{f}(\mathbf{x}) = \sum_{i=1}^p\lambda_i f_i(\mathbf{x}).$$
Each $\lambda_i$ acts as a weight on the $i$th objective, with the most important being given the most weight. However, how does one choose
weights? In some cases this may be obvious, but some may be much harder to decide. Also, what if the units of the objectives don't match?
After all, summing £s and g/km doesn't make sense. There is another fundamental problem with this idea. If $Y$ is not convex, then it may
not be possible to find all of the most interesting points. In the diagram, two objectives are considered, $f$ and $g$, but there are many points of
interest that cannot be achieved.

Ant colonisation was one heuristic approach mentioned by Epitropakis. It mimics the use of feromones ants leave to point towards a good
path.
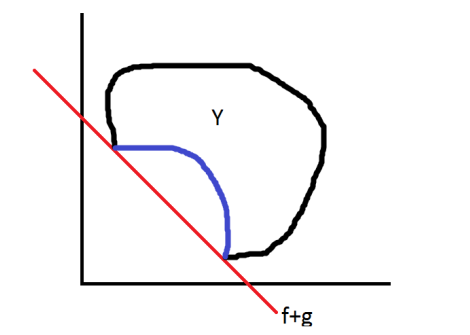
The diagram shows the region $Y$, and the red line is the equal weighted sum, $f+g$. However, it doesn't matter what other weightings I try, I cannot achieve any of the points in blue. This is due to the fact that a line tangent to a blue point must also pass through $Y$ at another point. As these points are not on the border, that line could be moved closer to the origin and thus reduce $f+g$. The blue points may be of great interest as they lie on the border. The problem occurs because $Y$ is not convex.
Our final talk was on Conic programming. This was given by Adam Letchford, who described the problem as a generalisation of Linear Programming. First a little bit of background on cones. A cone, $\mathcal{C}\subset\mathbb{R}^n$, is defined such that if $x\in\mathcal{C}$, then $\lambda x\in\mathcal{C}$ for all $\lambda>0$. In particular, we are interested in pointed and symmetric cones (in 3 dimensions it looks like an ice cream cone). Many different shapes and curves can be made by intersecting hyperplanes with cones. Circles can be made if the plane is normal to the cone axis, hyperbolae if the plane is parallel to the axis, and inbetween are ellipses and parabolas. In $\mathbb{R}^n$, a second order cone is one that satisifies $$x_n = \sqrt{x_1^2 + ... + x_{n-1}^2}.$$
What, you may ask, have cones and intersections and shapes got to do with optimisation? A Conic Programme is an optimisation problem
of the form
$$\text{inf}\left\lbrace c^Tx : Ax \leq b , x\in\mathcal{C}\right\rbrace.$$
The restriction to the cone, if a hyperplane is chosen well, is equivalent to the inclusion of a quadratic or hyperbolic constraint, such as
the one above, as well as the linear constraints. This now means that an optimum solution can be found to the problem, as in the
case of linear programming. The use of the second order cone equation as a constraint makes this a Second Order Cone Program (SOCP). There are
also other forms of conic programming that can be used.
Importantly, this is far better than other non-linear programming methods, which only approximate the optimum, for the particular
problems it is applicable to. However, whereas
currently LPs can be used for 10$^5$ variables pretty quickly, SOCP can only be used on about 1000 variables. And where as
the LPs can be solved in $\mathcal{O}(n^3)$ time, SOCPs have an order of $\mathcal{O}(n^4)$. It is still polynomial, but if you can
get away with an LP, you probably should. I think Conic Programming appeals to me as it is cleverly using mathematical structures to
solve problems a little beyond the scope of linear programming in an exact and rigorous way.

That sums up the talks on Optimisation. I hope the remaining seesions will be as interesting, and hopefully I can report on some of those
later in the week.