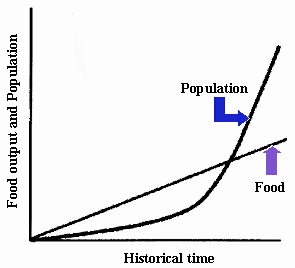
Continuous change that either accelerates or decelerates so that the pattern of change is curvilinear [J-shaped or S-shaped (sigmoid)]. A snowball rolling downhill changes exponentially with time since when it is twice as big, it gathers snow twice as fast. A prime example of exponential change is contained in the theory of population pressure devised by Thomas R. Malthus (1766-1834) as shown in the figure below: food production increases as a linear function (or what he called an ‘arithmetical ratio’) over historical time while a population changes exponentially (or what he termed as a ‘geometrical ratio’).