A mathematical term for an instability or transition in a non-linear dynamical system. In such a system, it is a qualitative change in its behavior (order parameter) from one attractor state to another due to a quantitative change at some critical level (a far-from-equilibrium condition) in one or more continuously varying control parameters. Where this change takes place is referred to as the bifurcation point (see figures A-F below for an example of successive bifurcation points).
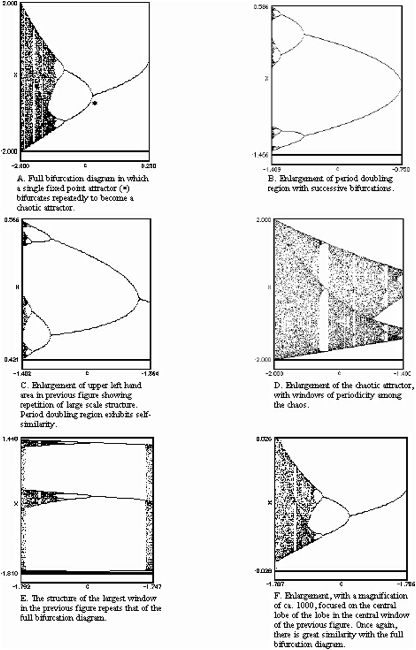
Changes from a fixed-point attractor to a chaotic attractor, via a succession of bifurcation points. When local areas in the full bifurcation diagram are magnified, the same underlying structure is revealed. In a sense then, the more things change at each bifurcation point, the more they stay the same (something referred to as ‘self-similarity’)
See Attractor, Catastrophe theory, Chaos, Control parameter, Dissipative system, Dynamical system, Instability, Irreversible thermodynamics, Non-linear dynamical systems, Order parameter, Phase transition (or shift), Qualitative and quantitative change, Transition
