Sam Close

Physics (Bailrigg) | Year 4 | Degree: Theoretical Physics MPhys Hons

Electromagnetic Pasta

Electromagnetism is a very well-studied topic at this point, however, that does not mean there is not more to uncover, or more approaches to take.

Based on recent work, this project looks at electromagnetism in the language of differential geometry, in a simpler space than the four-dimensional spacetime we normally consider. In lower dimensions, one can split the regular mathematical objects we work with into different ‘forms’, which were blessed with the names of pasta in the aforementioned recent work.

These pastas are interesting to analyse, since they need not always obey causality which makes them unintuitive to our causal brains. Similarly, one can ask questions about these pastas interacting with one another: what does interaction mean, and what are the dynamics?

The project also delves into visualising these pastas pictorially, allowing for a pictorial way of solving electromagnetic problems.

Sam Close

More information

Sam Close

Physics (Bailrigg) | Year 4 | Degree: Theoretical Physics MPhys Hons

Electromagnetic Pasta

It can be argued quite convincingly that most things we experience are governed by electromagnetic phenomena. These phenomena are described entirely by Maxwell's equations: linear, partial-differential equations. These equations and the accompanying theory have been extremely useful and succesful, as demonstrated by all modern technology. We can, however, reduce our equations to just two¹, using methods of differential geometry.

Maxwell's equations in the language of differential geometry

The detailed mathematics are beyond the scope of this poster, but suffice to say those equations look nice. As the name suggests (c.f., 'geometry'), these equations now encode something physical, which we can consider pictorially. We can split these symbols up into 'pasta', named² since in three-dimensions they look like spaghetti and lasagne.

The goal of the project was to consider the motion of these pastas numerically to see if one could solve Maxwell's equations pictorially.

The code was written using Maple, a symbolic language, as a proof of concept. Below are some example outputs.

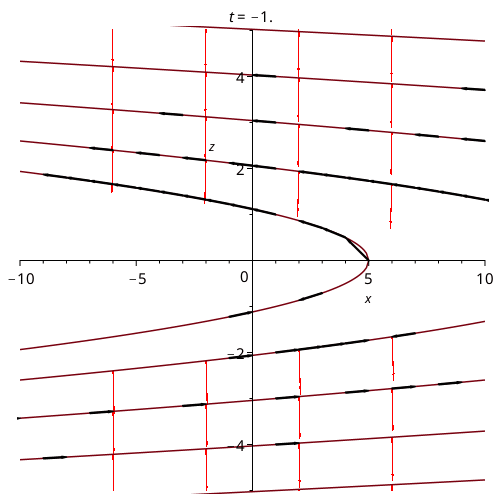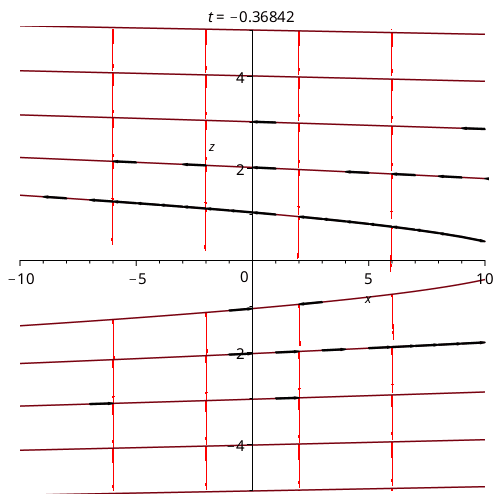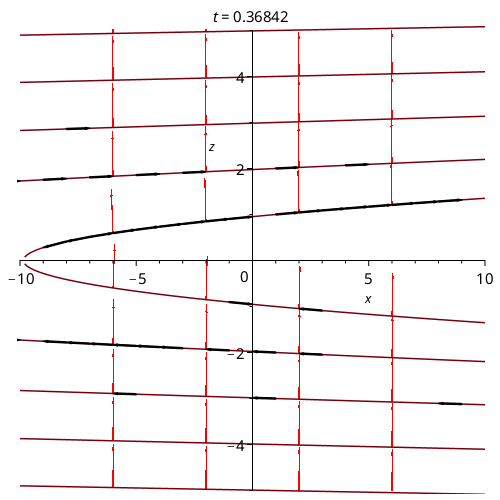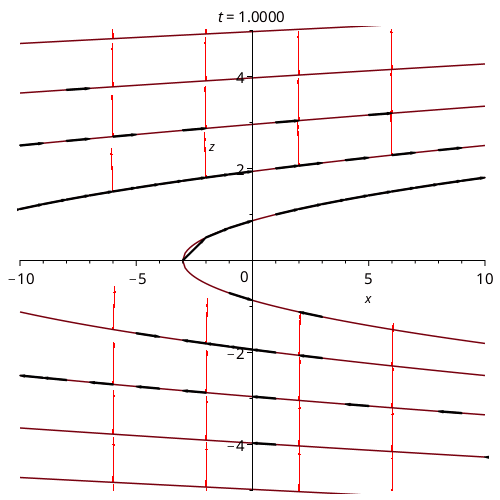
A gif showing moving lasagne of a point charge

This animation shows a real system of a point charge moving along the curve (t/8,1,0) in Cartesian Coordinates. One can now see the black arrows along the line, which tell you how the function is changing along the curve.

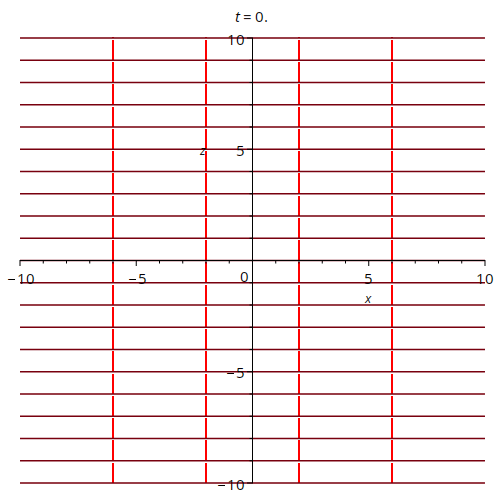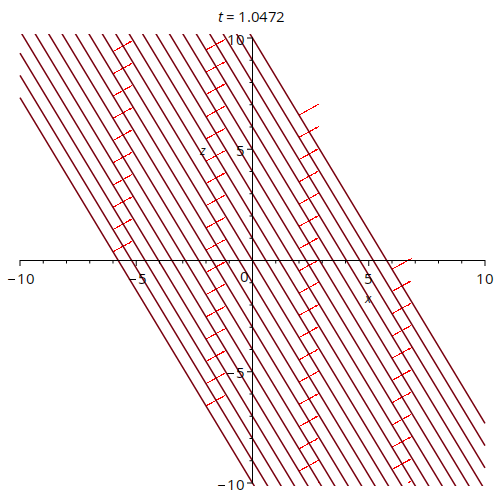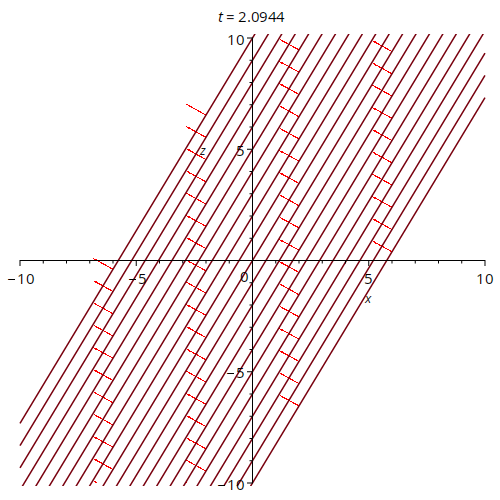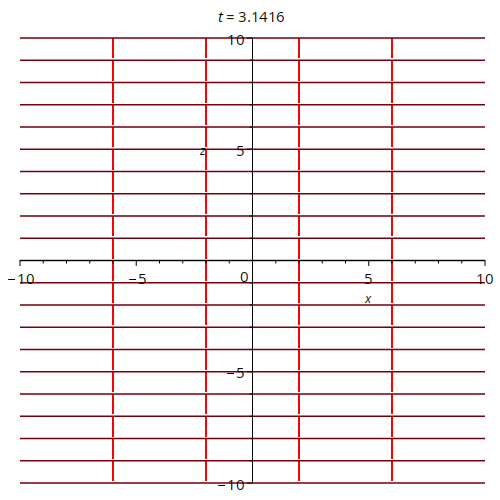
A plot showing the rotating lasagne generated by an oscillating electric field

This animation shows a very simple case of an electric field oscillating out of phase in the x- and z-axes. All units are arbitrary. The arrows tell one the orientation of the pasta. This particular example could be seen as modelling two perpendicular oscillating electric fields.

Another part of the procedure was to make a so-called 'top-form' plotter. A top-form, for our purposes, can be thought of as just points in the plane. These, for an electromagnetic system encode charge density. Whilst not as developed as the line code, an example result is shown below.

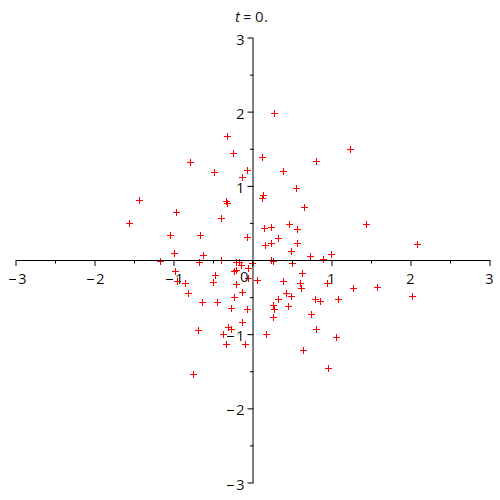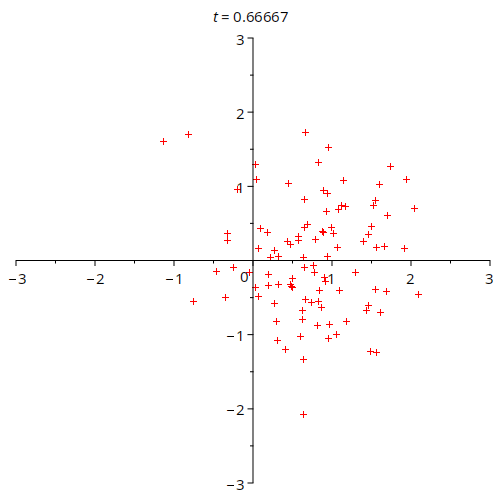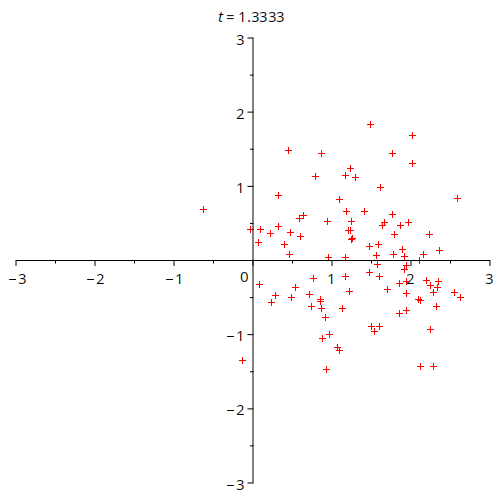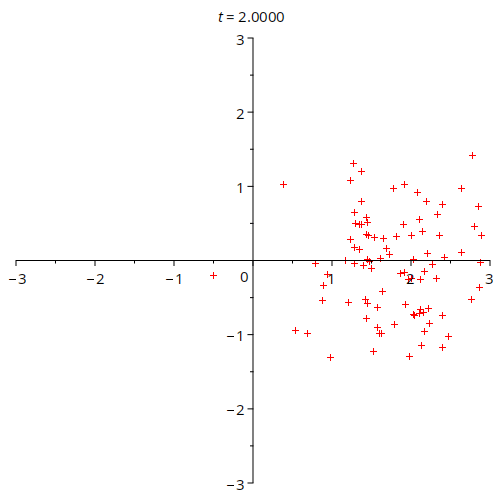
Animation showing a charge density moving in the x-direction

This animation shows a double gaussian charge density moving along the x-axis. The density of the dots tells one about the charge density, but note the dots do not tell you the exact position of the charges.

This method does have the potential to change how electromagnetic phenomena are simulated, since it gives a very clear geometric picture of the dynamics. We think the theory has potential to aid understanding of electromagnetic phenomena, since it is easier to show in two-dimensions than three.

Further development is needed to add interaction of the lines and dots to truly show the dynamics. Ongoing work is to add another type of line which is more representative of most electromagnetic phenomena, and to show the time evolution of points.

¹ There are strictly three equations which govern electromagnetic phenomena, the other being the Lorentz force, though that is not relevant for this project.

² Nomenclature introduced by Yakovleva M. Novel concepts for theoretical and applied problems of electromagnetism. Part 1 : Absolute representation of the fields in the spacetime map. Part 2 : Low-volume optical antennas for bolometer applications. University of Paris-Saclay; 2021. Available from: http://www.theses.fr/2021UPASP129.

Page saved!

Add default layout Add text Add image/symbol Add audio/video

PAUSE AUDIO PAUSE VIDEO