Boning Li

Computer Science (BJTU) | Year 4 | Degree: Computer Science

Implementing a Universal Turing Machine in Cellular Automata

The aim of this project is to implement a Universal Turing Machine (UTM) in a Cellular Automaton called The Game of Life. The Turing Machine is a powerful model of computation which is capable of doing anything that a general computer can do. More precisely, a Turing Machine can be used to simulate any existing algorithm. Through this project, I can get a better understanding of the theory of computation which provides the basic, fundamental concepts that permeate the whole field of computer science. By investigating this, we can develop more advanced models for understanding the nature of the Church-Turing thesis.

In this presentation, we will demonstrate an implementation of the Game of Life in both Java and Golly. The latter is a free and publicly available software platform that provides a set of Python libraries for the simulation of emergent computations. Such a platform serves as a tool for the implementation of a UTM in the Game of Life. For this, we have implemented a pattern called glider collision, and we have successfully constructed two logic gates with it.

Boning Li

More information

Boning Li

Computer Science (BJTU) | Year 4 | Degree: Computer Science

Implementing a Universal Turing Machine in Cellular Automata

What is (Universal) Turing Machine?

Turing Machine (TM) is a mathematical model that is able to do whatever a general computer can do. So, it can simulate any existing algorithm. For Universal Turing Machine (UTM), it is one that can simulate any other Turing Machines.

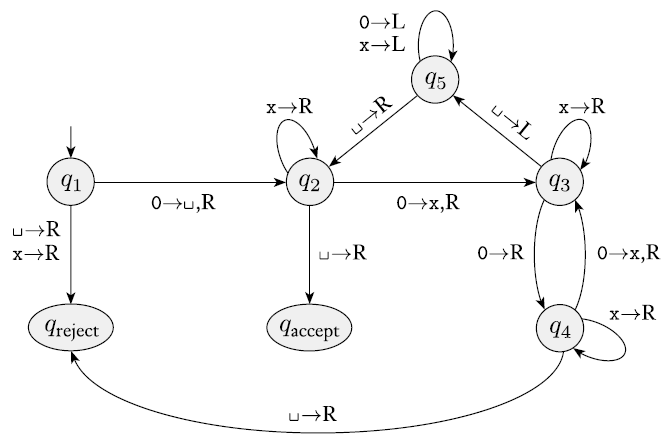
Formally, the Turing Machine is defined as a 7-tuple (Q, Σ, Γ, δ, q₀, q_accept, q_reject), where Q is the set of states, Σ is the input set without black symbol ␣, Γ is the tape set containing ␣, and δ is the ransition function from Q×Γ to Q×Γ×{L, R}. The other three are elements in Q and are the start state, accept state and reject state (not equal to q_accept), respectively.

Figure 1 shows an example TM together with its transition function. Here, the start state is q₁.

Figure 1. sample of Turing Machine [1]

Cellular Automaton -- The Conway's Game of Life

Cellular Automata (CA) are dynamic models to simulate the process of time-space evolution, and the Conway's Game of Life (GoL) is just one of them. A cellular automaton consists of a set of cells and rules. Each cell has its states and the rules define how these states will change from one to another simultaneously.

In the 2D cellular automaton Conway's Game of Life, cells have two states representing alive and dead, respectively, and 8 neighours around them. Its rules are quite simple. When a living cell has 2 or 3 living neighbours, it will keep alive, and will die in other cases. For a dead cell, it will trun to living when exactly 3 of its neighbours are alive, otherwise it just stays dead. The fowlloing figure displays one population for a 96×96 GoL written with JavaFX.

Figure 2. one population of GoL

In fact, there are some regular patterns in GoL, such as oscillators which repeat themselves in a fixed number of generations, and ships that move orthogonally. Partterns mainly used in this project are gliders and glider guns, just shown in the following figure. They will be used to construct logic gates.

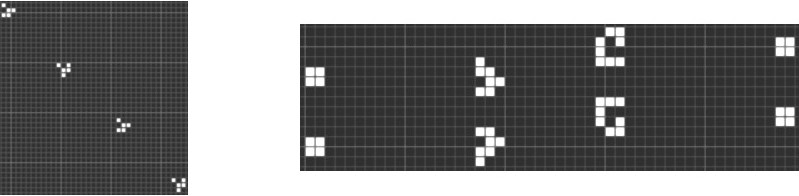
Figure 3. gliders (left) and glider gun (right)

How to implement UTM in the Game of Life?

Conclusively, Cellular Automata are equivalent to Universal Turing Machine, or alternatively, CA are Turing-complete. One way to demonstrate this equivalence is to find a mapping relation between their configurations.

Also, this equivalence can be proved by implementing various computational procedures such as logic gates in Game of Life. For example, the implementation of AND gate and NOT gate is shown in the figure below.

Figure 4. NOT gate (left), AND gate (right)

NOT gate is represented by the glider gun on the right side, and the left gun is used as the input. When the input comes to the gate, two gliders will collide with each other and disappear, and as a result, the output is 0 (just no glider). Otherwise, the glider shot by the gate will keep on going and the output is 1 (opposite to 0). AND gate works in a similar way, except that there are two input guns.

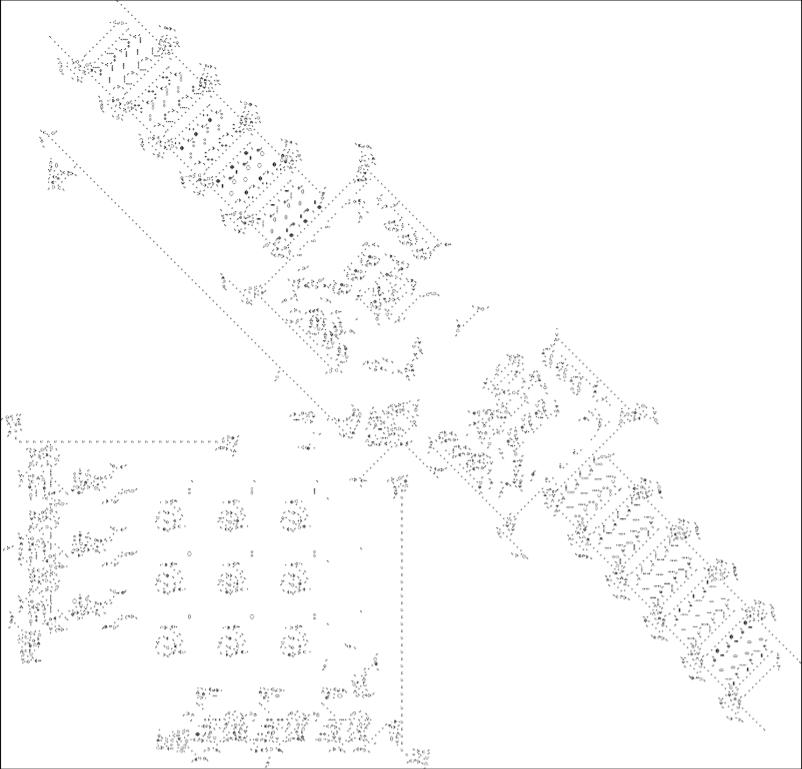
Rendell (2001) successfully implemented a complete Turing Machine in the Game of Life, which is shown in the following figure. He explained how to used gliders to represent the data in memory and control the stack. The original paper can be accessed through clicking the arrow at the bottom right corner.

Figure 5. Rendell's implementation [3]

Bibliography

Sipser, M. (2012). The Church-Turing Thesis. Introduction to the Theory of Computation, Third Edition. Stamford: Cengage Learning, 2012. pp. 165-187.
Mitchell, M. (1996). Computation in Cellular Automata: A Selected Review.
Rendell, P. (2001). A Turing Machine In Conway's Game Life. Available at: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.386.7806&rep=rep1&type=pdf [Accessed on Feb. 25, 2022].

Page saved!

Add default layout Add text Add image/symbol Add audio/video

PAUSE AUDIO PAUSE VIDEO