Home page for accesible maths 14 Distribution of the MLE Exam Question 14.2 Summary

Style control - access keys in brackets

Font (2 3) - + Letter spacing (4 5) - + Word spacing (6 7) - + Line spacing (8 9) - +

Solution:

a
There are 3 types of component, each giving rise to a constraint on $\theta$ :
1. 1
  
  $0\leq\theta\leq 1$ ,
2. 2
  
  $0\leq 3\theta\leq 1$ ,
3. 3
  
  $0\leq 1-4\theta\leq 1$ ,
as the components each need to have valid probabilities. The third inequality is sufficient for the other two and gives $0\leq\theta\leq 1/4$ .
b

Given the data, the likelihood is

$\displaystyle L(\theta)$ $\displaystyle\propto\theta^{2}(3\theta)^{5}(1-4\theta)^{43}$

$\displaystyle\propto\theta^{7}(1-4\theta)^{43}.$

For the sketch note that $L(0)=L(1/4)=0$ and the function is concave and positive between these two with a maximum closer to $0$ than $1/4$ .
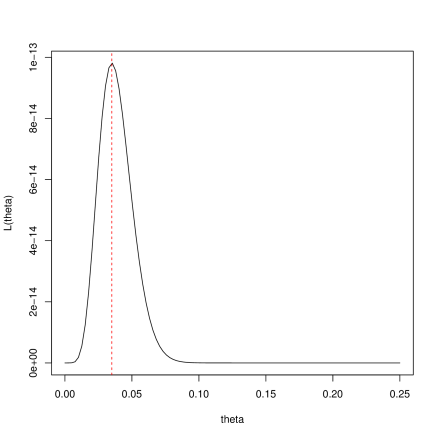
c

To work out the MLE, we differentiate the (log-)likelihood as usual. The log-likelihood is

$l(\theta)=7\log\theta+43\log(1-4\theta).$

Differentiating,

$l^{\prime}(\theta)=\frac{7}{\theta}-\frac{4\times 43}{1-4\theta}.$

A candidate MLE solves $l^{\prime}(\hat{\theta})=0$ , giving $\hat{\theta}=\frac{7}{200}$ .

Moreover,

$l^{\prime\prime}(\theta)=-\frac{7}{\theta^{2}}-\frac{4\times 4\times 43}{(1-4% \theta)^{2}}<0,$

so this is indeed the MLE.
d

The observed information is

$\displaystyle I_{O}(\hat{\theta})$ $\displaystyle=-l^{\prime\prime}(\hat{\theta})$

$\displaystyle=\frac{7}{\hat{\theta}^{2}}+\frac{4\times 4\times 43}{(1-4\hat{% \theta})^{2}}$

$\displaystyle=5714.3+930.2$

$\displaystyle=6644.5.$

So a $95\%$ confidence interval for $\theta$ is

$\left(\hat{\theta}-\frac{1.96}{\sqrt{I_{O}(\hat{\theta})}},\hat{\theta}+\frac{% 1.96}{\sqrt{I_{O}(\hat{\theta})}}\right)$

$=(0.0110,0.0590).$

As $0.02$ is within this confidence interval there is no evidence of this batch being sub-standard.

	$\displaystyle L(\theta)$	$\displaystyle\propto\theta^{2}(3\theta)^{5}(1-4\theta)^{43}$
		$\displaystyle\propto\theta^{7}(1-4\theta)^{43}.$

	$\displaystyle I_{O}(\hat{\theta})$	$\displaystyle=-l^{\prime\prime}(\hat{\theta})$
		$\displaystyle=\frac{7}{\hat{\theta}^{2}}+\frac{4\times 4\times 43}{(1-4\hat{% \theta})^{2}}$
		$\displaystyle=5714.3+930.2$
		$\displaystyle=6644.5.$