Home page for accesible maths 3 Functions of two or more variables 3 Functions of two or more variables 3.2 The gradient vector

Style control - access keys in brackets

Font (2 3) - + Letter spacing (4 5) - + Word spacing (6 7) - + Line spacing (8 9) - +

3.1 Some examples

Typical functions of two, three or four variables are:

f(x,y)=x^{2}+y^{2},\qquad f(x,y,z)=x(y^{2}-z^{2}),\qquad f(x,y,z,t)=(x^{2}+y^{% 2}+z^{2})e^{-t}.

Such functions arise constantly in applications to real-world problems. Usually, $(x,y,z)$ represents a point in space and $t$ (if present) represents time. But mathematically, the variables are just neutral numbers: a function of three variables is just a function on $\mathbb{R}^{3}$ , the set of all ordered triples $(x,y,z)$ .

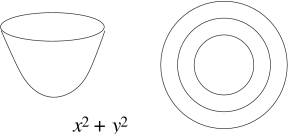
Geometrical representation. The equation $z=f(x,y)$ defines a surface in three dimensions. We can try to draw it (which isn’t always easy!), or we can draw the contours $f(x,y)=c$ in the $(x,y)$ -plane, as is done on maps (as shown below). The contours are therefore “implicitly-defined functions” as described in the previous section.

If $g$ is a function of three variables, then for each $c$ , the equation $g(x,y,z)=c$ again describes a surface: these are called the level surfaces of $g$ . The previous example $z=f(x,y)$ is the special case where $g(x,y,z)=f(x,y)-z$ and $c=0$ . A simple case: $ax+by+cz=h$ is a plane.

Of course, following the formulation of a parametrized curve given in the previous section, we ought to be similarly precise about what a surface is. Indeed, we can define a parametrized surface in ${\mathbb{R}}^{3}$ as a continuous map $\varphi:I\rightarrow{\mathbb{R}}^{3}$ , where $I\subset{\mathbb{R}}^{2}$ is an appropriate set. The problem is defining what an ‘appropriate set’ is. We won’t go into the definition of such a set; in this course, any “reasonable” choice of $I$ can be considered acceptable.

Parametrized curves and surfaces are particular examples of vector-valued functions. Similarly, we could define vector-valued functions in ${\mathbb{R}}^{3}$ or ${\mathbb{R}}^{4}$ .

Example 3.1 Suppose an object of mass $M$ is at the origin. The gravitational force exerted on a unit mass at position ${\bf r}=(x\;\;y\;\;z)$ is:

\frac{GM}{|{\bf r}|^{2}}\cdot\frac{-{\bf r}}{|{\bf r}|}

Here the formula $F=GM/r^{2}$ is well-known from Newtonian mechanics; the expression $-{\bf r}/|{\bf r}|$ is a unit vector towards the origin. The force is a vector-valued function, depending on $x, y, z$ but undefined at $(x\;\;y\;\;z)=(0\;\;0\;\;0)$ .

Example 3.2 Suppose the object of mass $M$ has position $\gamma(t)=(X(t)\;\;Y(t)\;\;Z(t))$ at time $t$ . Then the gravitational force exerted on a unit mass at position ${\bf r}=(x\;\;y\;\;z)$ and time $t$ is:

\frac{GM}{|{\bf r}-\gamma(t)|^{2}}\cdot\frac{-({\bf r}-\gamma(t))}{|{\bf r}-% \gamma(t)|}

This is a vector-valued function which depends on $x, y, z$ and $t$ (and is undefined at the point $(X(t),Y(t),Z(t))$ at time $t$ ).

Generally, we shall assume that our functions vary continuously except perhaps at isolated points. The following example shows the sort of thing that can happen near a discontinuity.

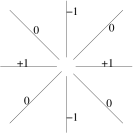
Example. Let $\displaystyle{f(x,y)=\frac{x^{2}-y^{2}}{x^{2}+y^{2}}}$ except at $(0,0)$ . On each straight line $y=\lambda x$ , $f(x,y)$ has the constant value $(1-\lambda^{2})/(1+\lambda^{2})$ (in particular, 1 on the $x$ -axis and $-1$ on the $y$ -axis). We could define a surface $z=f(x,y)$ in ${\mathbb{R}}^{3}$ , but it’s quite hard to visualize the surface near the $z$ -axis !