Home page for accesible maths 4 Discrete random variables 4.4 Expectation 4.6 Chebychev’s inequality

Style control - access keys in brackets

Font (2 3) - + Letter spacing (4 5) - + Word spacing (6 7) - + Line spacing (8 9) - +

4.5 Variance

Expectation is a weighted average, and consequently is a measure of the location of the pmf. The spread, or dispersion, of a random variable is usually measured by the variance: the expected squared deviation about the expectation.

The variance of the random variable ${R}$ , ${{\rm Var}(R)}$ , is defined as $\displaystyle{\rm Var}(R)={\rm E}[(R-{\rm E}[R])^{2}],$ The standard deviation of ${R}$ , ${{\rm s.d.}(R)}$ , is defined to be the square root of the variance.

The variance is the expectation of the function of the random variable ${g(R)=(R-m)^{2}}$ , where ${m={\rm E}(R)}$ is a number.

Aside: To get a feel for standard deviations experience (and some nice theory in later courses!) suggests that for many random variables approximately ${95\%}$ of the probability mass falls within ${\pm 2}$ standard deviations of the mean of the random variable.

Exercise 4.22.

Suppose that four random variables ${R_{1}}$ , ${R_{2}}$ , ${R_{3}}$ and ${R_{4}}$ on ${{\mathcal{S}}=\{0,1,2\}}$ have pmfs

{\begin{array}[]{r|rrr}&0&1&2\\ \hline p_{1}(r)&0&1&0\\ p_{2}(r)&1/4&1/2&1/4\\ p_{3}(r)&1/3&1/3&1/3\\ p_{4}(r)&1/2&0&1/2\\ \hline\end{array}}

respectively. These are plotted in the graphs:

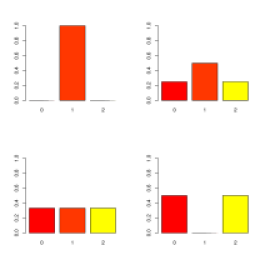
Note for each pmf the sum of the probs is ${1}$ . The expectations are the same so that

{{\rm E}[R_{1}]={\rm E}[R_{2}]={\rm E}[R_{3}]={\rm E}[R_{4}]=1}.

Find the variances.

Solution.

The different variances are

{\begin{array}[]{llll}(0-1)^{2}\times 0&+(1-1)^{2}\times 1&+(2-1)^{2}\times 0&% =0,\\ (0-1)^{2}\times 1/4&+(1-1)^{2}\times 1/2&+(2-1)^{2}\times 1/4&=1/2,\\ (0-1)^{2}\times 1/3&+(1-1)^{2}\times 1/3&+(2-1)^{2}\times 1/3&=2/3,\\ (0-1)^{2}\times 1/2&+(1-1)^{2}\times 0&+(2-1)^{2}\times 1/2&=1.\end{array}}

We see that ${{\rm Var}[R_{1}]<{\rm Var}[R_{2}]<{\rm Var}[R_{3}]<{\rm Var}[R_{4}]}$ . This agrees with intuition of dispersions from barplots.

This formulation of the variance is inconvenient for calculation, so alternative forms have been derived which simplify evaluation. Writing ${{\rm E}[R]}$ as ${m}$ a constant, we have

$\displaystyle{\rm Var}(R)$	$\displaystyle=$	$\displaystyle{\rm E}[(R-{\rm E}(R))^{2}],{\mbox{\color[rgb]{1,1,1}\quad def}}$
	$\displaystyle=$	$\displaystyle{\rm E}[(R-m)^{2}],{\mbox{\color[rgb]{1,1,1}\quad rewrite}}$
	$\displaystyle=$	$\displaystyle{\rm E}[R^{2}-2Rm+m^{2}],{\mbox{\color[rgb]{1,1,1}\quad expand}}$
	$\displaystyle=$	$\displaystyle{\rm E}[R^{2}]-2{\rm E}[mR]+{\rm E}[m^{2}],{\mbox{\color[rgb]{% 1,1,1}\quad linearity}}$
	$\displaystyle=$	$\displaystyle{\rm E}[R^{2}]-2m{\rm E}[R]+m^{2},{\mbox{\color[rgb]{1,1,1}\quad$% {{\rm E}}$ const}}$
	$\displaystyle=$	$\displaystyle{\rm E}[R^{2}]-2mm+m^{2},{\mbox{\color[rgb]{1,1,1}\quad def ${m}$% }}$
	$\displaystyle=$	$\displaystyle{\rm E}[R^{2}]-m^{2},{\mbox{\color[rgb]{1,1,1}\quad simplify }}$
	$\displaystyle=$	$\displaystyle{\rm E}[R^{2}]-({\rm E}[R])^{2},{\mbox{\color[rgb]{1,1,1}\quad rewrite% .}}$

Exercise 4.23.

Find the variance of a random digit ${R}$ uniformly distributed on the integers ${r=1,2,\dots,6}$ .

Solution.

From above ${{\rm E}(R)=\frac{7}{2}}$ , and

{{\rm E}(R^{2})=\frac{1}{6}1^{2}+\frac{1}{6}2^{2}+\cdots+\frac{1}{6}6^{2}=% \frac{91}{6}.}

\displaystyle{\rm Var}(R)

\displaystyle=

\displaystyle{\rm E}(R^{2})-[{\rm E}(R)]^{2}=\frac{91}{6}-[\frac{7}{2}]^{2}=% \frac{35}{12}

As with linearity for expectation there is an important result for the variance of linear functions of a random variable $R$ . Suppose ${a}$ and ${b}$ are constants

$\displaystyle{\rm Var}(aR+b)$	$\displaystyle=$	$\displaystyle{\rm E}[(aR+b-{\rm E}[aR+b])^{2}]\mbox{\color[rgb]{1,1,1}\quad def% ${{\rm Var}}$}$
	$\displaystyle=$	$\displaystyle{\rm E}[(aR+b-(a{\rm E}[R]+b))^{2}]\mbox{\color[rgb]{1,1,1}\quad lin% ${{\rm E}}$}$
	$\displaystyle=$	$\displaystyle{\rm E}[(aR-a{\rm E}[R])^{2}]\mbox{\color[rgb]{1,1,1}\quad factor}$
	$\displaystyle=$	$\displaystyle{\rm E}[a^{2}(R-{\rm E}[R])^{2}]\mbox{\color[rgb]{1,1,1}\quad factor}$
	$\displaystyle=$	$\displaystyle a^{2}{\rm E}[(R-{\rm E}[R])^{2}]\mbox{\color[rgb]{1,1,1}\quad lin% ${{\rm E}}$ }$
	$\displaystyle=$	$\displaystyle a^{2}{\rm Var}(R).\mbox{\color[rgb]{1,1,1}\quad def ${{\rm Var}}$}$

This result shows the important properties of variance:

	$\displaystyle{\rm Var}(R+b)$	$\displaystyle=$	$\displaystyle{\rm Var}(R)$
	$\displaystyle{\rm Var}(aR)$	$\displaystyle=$	$\displaystyle a^{2}{\rm Var}(R).$

Exercise 4.24.

For a random variable ${R}$ , ${{\rm E}[R]=3}$ and ${{\rm Var}(R)=2}$ . Find

i.

${{\rm E}[2R]}$
ii.

${{\rm E}[-2R+6]}$
iii.

${{\rm Var}(2R)}$
iv.

${{\rm Var}(-2R+6)}$

Solution.

i.

${{\rm E}[2R]=2{\rm E}[R]=6}$ .
ii.

${{\rm E}[-2R+6]=-2{\rm E}[R]+6=0}$ .
iii.

${{\rm Var}(2R)=2^{2}{\rm Var}(R)=8}$ .
iv.

${{\rm Var}(-2R+6)=(-2)^{2}{\rm Var}(R)=4{\rm Var}(R)=8}$ .

In summary

$\displaystyle{\rm Var}(R)$ $\displaystyle=$ $\displaystyle{\rm E}[(R-{\rm E}(R))^{2}]$ $\displaystyle=$ $\displaystyle{\rm E}[R^{2}]-({\rm E}[R])^{2},$ $\displaystyle{\rm Var}(aR+b)$ $\displaystyle=$ $\displaystyle a^{2}{\rm Var}(R),$